浅埋土质大断面隧道下穿高速公路变形控制技术研究

王 成,林森斌

(铁道第三勘察设计院集团有限公司,天津 300251)

随着城市规划的日趋完善，地下工程如地下铁道、公路隧道等作为城市规划的重要部分，显得尤为重要。但受到城市规划空间的限制，涌现出越来越多的复杂隧道。

城市道路纵横交错，且车流量与日俱增，隧道在下穿道路时如何确保道路正常使用及行车安全是目前设计、施工的难点。以山西某铁路隧道下穿市区环城高速公路为研究背景，采用三维数值模拟法分析不同荷载及速度的车辆在行驶时与隧道施工的相互影响，在变形控制方面取得了一些有益的结论。

1 工程概况及设计简介

以山西某铁路隧道工程为例。隧道范围内地面建筑物密集，主要类型为民居、工厂建筑，沿线经过大量村庄、市区公路、高速公路，近距离侧穿受保护建筑物。根据覆土厚度及地质条件，本隧道属浅埋、土质隧道，采用明、暗法相结合的方法施工。本次研究段落内隧道采用暗挖法施工，采用单洞双线隧道，线间距5 m，隧道内设双侧救援通道，救援通道宽1.25 m(自线路中线外1.7 m起算)、净高2.2 m，隧道开挖面积约131 m2。隧道下穿环城高速公路路宽24 m(双向6车道)，与线路走向成147°夹角，隧道结构顶距离高速公路路面约7.5 m。穿越区域地层主要为素填土、新黄土、粉质黏土和圆砾土层，地下水位在隧道仰拱底以下。

为控制路面变形，设计采用在隧道拱部140°范围内采用φ159 mm双层大管棚超前加强支护，管棚长120 m；每层管棚环向间距0.4 m，层间距0.3 m，呈梅花形布置。管棚内填充水泥浆，管棚之间架设小导管，采用φ42 mm、t=3.5 mm热轧钢管，环向3根/m，纵向两榀格栅1环，施工外插角10°～15°。隧道上半断面均采用玻纤锚杆稳定掌子面，玻纤锚杆垂直于掌子面打入，锚杆长度为12 m，锚杆每列间距60 cm，行间间距80 cm。隧道开挖方法采用CRD工法，开挖完毕后立即喷射C30早强混凝土，采用HW175型钢支撑，间距0.5 m/榀。

根据高速公路评估结果及其管理单位要求，高速公路运营过程中，路面允许最大沉降值不超过30 mm，并设置预警值(65%极限值)、报警值(85%极限值)、极限值三级控制，施工过程中全程监测。

2 不同行车条件下地表变形三维数值模拟与实测数据分析

2.1 模型概况

通过建立三维有限元地层-结构模型模拟隧道下穿环城高速公路段落。模型四周及底部取法向约束，顶部为自由面；模拟隧道实际施工工序，不仅要考虑到周边土体的复杂特性和施工作业方式(包括CRD工法的开挖工序、支护结构形式)，还要考虑开挖面推进过程中的空间效应及地层应力释放等因素。高速公路车辆荷载，根据相关公路规范取值。三维有限元地层-结构模型如图1所示，路面地表测点布置如图2所示。

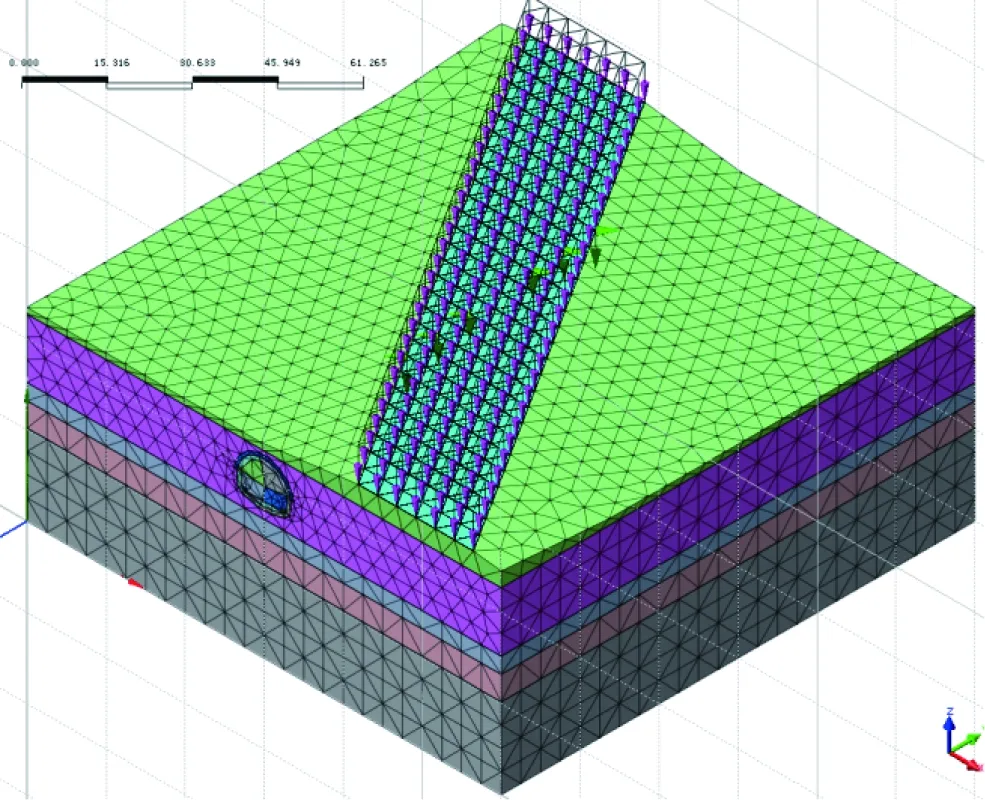
图1 地层-结构模型等轴侧视图

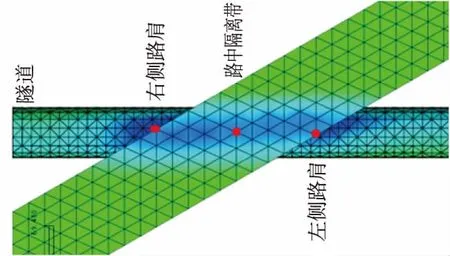
图2 路面地表测点布置(仅示隧道中线方向)

2.2 不同行车荷载、速度条件下地表变形分析

本次模拟按正常使用工况假定行车道及超车道仅限小中型车行驶，时速120 km；慢车道仅限大型车行驶，时速80 km，根据模拟结果得出图3所示的地表沉降曲线。当上述速度分别降为80 km/h与40 km/h时，地表沉降曲线如图4所示。

图3 正常车速行驶下地表沉降曲线

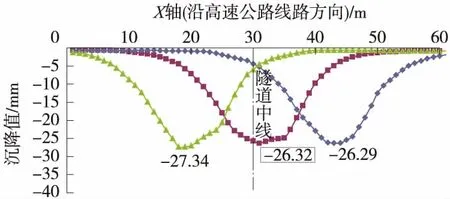
图4 降低车速行驶下地表沉降曲线

由图3可知，左、右侧路肩的最大沉降值始终大于中间隔离带处的最大沉降值。由于左、右侧路肩均位于重车道方向，故在重车的荷载作用下，随着隧道的开挖，其地表沉降值大于轻车道方向的沉降值。由图4可知，在不同行驶速度下，以左侧路肩为例，地表沉降最大值分别为29.30 mm与27.34 mm，行驶速度对地表沉降值具有一定的影响。

该路段处于曲线段，考虑车辆荷载在不同速度下产生的向心力，在该向心力的作用下产生的地表水平位移如图5所示(以左侧路肩处水平位移曲线为例)，正常行驶速度为80 km/h时，该处最大水平位移为11.65 mm；限速40 km/h时，该处最大水平位移为9.60 mm。根据以上结构，可以初步认为汽车在曲线上的行驶速度对路面水平位移具有一定的影响，速度越快(表现为向心力越大)，路面水平位移越大。

图5 左侧路肩处路面水平位移曲线施工步

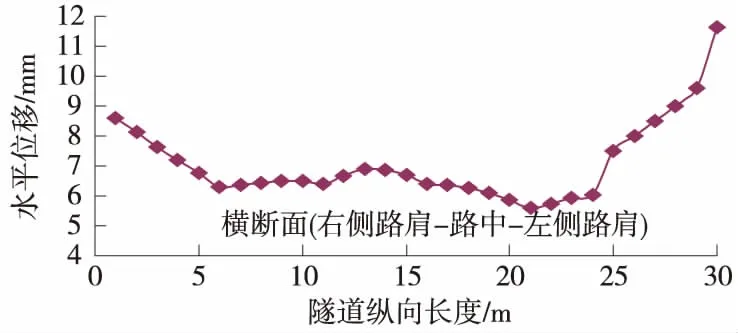
图6 隧道中心方向路面水平位移曲线

由图6可知，在行驶速度为120 km/h下，不同车荷载作用下产生的路面水平位移差异较大。其最大位移值发生在左侧路肩处，该处位于线路最大曲线半径处，且为重车方向，故其位移为11.65 mm，最小值发生在高速公路的隔离带，该处车荷载基本为零，其位移值最小，为6.41 mm。

结合现场实际情况，地表测点布置与图2一致，图7为实测地表沉降曲线，图8为现场地表裂缝情况。

图7 实测地表沉降曲线

图8 高速公路路面开裂情况

由图7可知，地表沉降最大位移发生在右侧路肩处，该行车方向重车密度大，在重车荷载的反复作用下，隧道开挖影响范围内，该侧路肩位移最大值为31.95 mm。地表沉降最小位移发生在左侧路肩处，该行车方向重车密度小，多为空车返回，隧道影响范围内发生的最大位移值为27.81 mm。实测地表沉降趋势基本与模拟结果吻合，由于隔离带处两侧均位于超车道，行车速度快且车流密度较大，使得其实测地表最大沉降值大于左侧路肩处最大沉降值。

伴随隧道掌子面的推进，地表逐渐出现1条细微裂缝，沿着掌子面的推进方向向前发展，并在仰拱封闭成环时裂缝宽度达到最大值，约为15 mm。当该裂缝扩展至行车道与超车道交界处，出现1条细微的纵向裂缝，当仰拱施作至此位置时，裂缝宽度达最大值，与横向裂缝交错处约为20 mm，裂缝两侧的路面出现错台，错台高差约为12 mm。该纵向裂缝沿着车辆行驶方向逐渐扩展，裂缝宽度逐渐变小，直至消失。实际行车过程中，重车主要行驶在行车道与慢车道，其实际产生的最大向心力位于行车道与超车道之间，即由图8所示的路面横向裂缝出现在行车道与超车道附近。

因该高速路段为该地区外环主要干道，实际行车荷载、速度与模拟取值具有一定的差异，其与地表沉降的关系可参考数值模拟结果中的相关内容。

3 仰拱封闭成环时间与地表沉降的关系

结合大多数工程经验，仰拱封闭成环作为隧道施工的关键步骤之一，在现代隧道施工中显得尤为重要，合理的仰拱封闭成环时间更是对环境敏感区域控制变形起到关键作用。图9为实测DK12+560处隧道上方的地表位移。由图9可知，采用CRD法分部开挖隧道各个断面时，地表累计沉降为10.78 mm。当开挖仰拱部分土体时，一次性开挖长度为8 m，至仰拱部分土体开挖完毕，地表累计沉降为29.02 mm，增量为18.24 mm，随着仰拱的浇筑封闭成环后，地表沉降增量逐渐趋于稳定，至二次衬砌浇筑前基本稳定在29.02 mm左右。

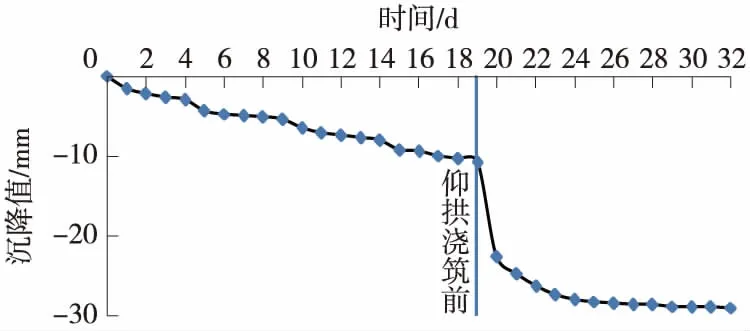
图9 DK12+560处隧道施工过程中地表沉降曲线

DK12+560正位于高速路坡脚处，由于变形过大，导致截水沟开裂。根据现场实测数据分析，结合图9可知主要变形发生在施作仰拱时，如何缩短仰拱封闭成环时间是控制变形的主要因素。结合现场实际情况，将原8 m施作一循环仰拱调整为每3 m施作一循环，图10为地表DK12+570处实测沉降值，分析可知在缩短仰拱循环步长、缩短其封闭成环时间可很好地控制地表沉降，经过施工步序调整，DK12+570处地表沉降最终控制在26.87 mm左右。随着掌子面向轻车道方向，地表沉降基本控制在27 mm左右。

图10 DK12+570处隧道施工过程中地表沉降曲线

4 结论与建议

(1)车辆荷载与行车速度对路面地表沉降影响较大，建议类似工程在条件允许时，尽量实行公路限速，并控制重车通过数量及频率；对于下穿该类高速公路路段施工时，控制行车速度是必要的，车辆在高速行驶的过程中产生的离心力加速地表裂缝的扩展，特别是贯通路面的纵向裂缝在该力的作用下容易发生错台，引发安全事故。

(2)仰拱封闭成环时间是控制地表沉降的关键因素，结合本文在仰拱施作循环长度的调整上得出的结论，建议对于后续类似工程，仰拱封闭成环的循环长度控制在3～5 m。

[1] 王建宇.隧道工程监测和信息化设计原理[M].北京：中国铁道出版社，1990．

[2] 黄宏伟.岩土工程中位移量测的随机逆反分析[J].岩土工程学报，1995，17(3)：36-41.

[3] 铁道第二勘察设计院.铁路工程设计技术手册— 隧道[M].北京：中国铁道出版社，1995.

[4] 朱合华，丁文其.地下结构施工过程的动态仿真模拟分析[J].岩石力学与工程学报，1999，18(5)：558-562.

[5] 谢和平，周宏伟，王金安.FLAC在煤矿开采沉陷预测中的应用及对比分析[J].岩石力学与工程学报，1999，18(4)：397-401.

[6] 麻永华，贺善宁.建筑物下浅埋暗挖隧道施工技术研究[J].铁道标准设计，2004(12).

[7] 王梦恕.地下工程浅埋暗挖技术通论[M].合肥：安徽教育出版社，2005.

[8] 蒋爵光.隧道工程地质[M].北京：中国铁道出版社，1991.

[9] 岳岭.超浅埋铁路隧道小角度下穿铁路沉降控制技术研究[J].铁道标准设计，2012(8)：80-82.

[10] 王春林.地铁隧道施工对地层变形的影响[J].科技资讯，2006(8)：36-38.

[11] 郭磊，帖卉霞，周钦.下穿高速公路铁路隧道对高速公路的影响研究[J].铁道标准设计，2010(5)：94-96.

[12] 郑战清.高速公路超浅埋下穿318国道施工技术[J].隧道建设，2005,25(4)：29-33.

[13] 刘和清.下穿高速公路的浅埋大断面隧道衬砌受力分析[J].铁道标准设计，2011(4)：95-97.