基于LS-DYNA的车辆对桥墩撞击力仿真分析

刘思明,崔堃鹏,夏 禾,张 楠

(北京交通大学土木建筑工程学院,北京 100044)

我国国民经济持续快速稳定发展，商品流通、人员往来等对交通的需求增长非常之快，越来越多的跨线桥梁投入使用或正在建设之中。而由于驾驶人员失误、预防工作不足、监管不力等原因，跨线桥下方车辆撞击桥梁的事故时有发生。2005年，一辆大型水泥罐车由于司机疲劳驾驶在穿行西固深沟桥双洞铁路桥时撞击桥墩，导致桥墩损坏；而在2008年1月29日，207国道襄城观音阁路段一大货车为避免与前行客车相撞，迎面撞上焦柳铁路立交桥桥墩。在车辆撞击荷载作用下，墩顶位移会使撞击位置的轨道不平顺增强，而桥梁的水平响应则成为车桥动力作用的激励源。这些都对桥梁的安全运营和使用寿命带来不利影响，留下灾难性事故隐患，甚至直接威胁列车运行安全，从而造成巨大的生命和财产损失。

车桥碰撞问题包括车撞桥墩和超高车辆撞击梁体两部分。目前，关于车辆撞击结构已有不少研究，如美国德克萨斯州运输研究所在足尺撞墩实验基础上，采用有限元分析研究了车速对撞击力的影响；再如澳大利亚昆士兰大学的H.M.I.Thilakarathna采用非线性数值分析模型，研究了车辆对墩柱的撞击作用[1]；此外还有Tsang[2]，Liu[3]，Macdonald[4]等人做了相关研究。本文主要研究对象为车与桥墩撞击，旨在探索不同载重下车桥撞击力变化规律。

1 有限元软件LS-DYNA

1.1 LS-DYNA基本原理

LS-DYNA是世界上著名的通用显示非线性动力分析程序，能够模拟真实世界的各种复杂问题。它具有强大的分析能力、丰富的材料模型库、易用的单元库以及自适应网格剖分等功能。特别适合求解几何非线性、材料非线性和接触非线性问题，如爆炸与冲击、结构碰撞、金属加工成形问题。它以显式分析为主，隐式分析为辅；以Lagrange算法为主，兼有ALE和Euler算法。其显示动力分析采用中心差分方法，结构系统各节点在第n个时间步结束时刻的加速度向量通过下式进行计算

a(tn)=M-1[P(tn)+Fint(tn)](1)

式中，P为第n个时间步结束时刻结构上所施加的节点外力向量(包括分布荷载经转化的等效节点力)；Fint为tn时刻的内力矢量，它由下面几项构成

σdΩ+Fhg+Fcontact(2)

上式右边3项依次为：tn时刻单元应力场等效节点力(相当于动力平衡方程内力项)、沙漏阻力Fhg(为克服单点高斯积分引起的沙漏问题而引入的黏性阻力)和接触力矢量Fcontact。根据中心差分法基本思路，加速度由速度的一阶中心差分给出，速度由位移的一阶中心差分给出。于是节点速度向量可由计算出的加速度结合差分公式表示，节点位移向量可由节点速度向量结合差分公式表示。

1.2 仿真分析过程

有限元仿真分析共有前处理、有限元求解和后处理3个阶段。在前处理中，需要制定分析所选用的单元类型、定义材料模型、创建几何模型、进行网格划分、定义PART、定义接触信息、边界条件和荷载等。在后处理中，可通过软件查看力、加速度、应力等变量的时间历程曲线。

作为求解器，LS-DYNA本身只用于读取模型信息、计算并输出结果，而不具备前处理与后处理功能，需要配合HYPERMESH、ANSYS或LS-PREPOST等前、后处理程序使用。本文选择LS-PREPOST与DYNA配合使用。

2 仿真模型的建立

2.1 车辆模型

与一般刚体或崩塌岩体撞击桥墩等情况不同的是，车辆(特别是车头部分)在撞击过程中产生变形并吸收能量。为了能够模拟车头的变形吸能，车辆模型采用由美国联邦高速公路(FHWA)和美国高速公路安全协议 (NHTSA) 支持的“国家碰撞分析中心”(National Crash Analysis Centre， NCAC)推出的双轴卡车有限元模型F800，如图1所示。该模型是基于LS-DYNA软件的标准汽车有限元模型系列之一，由联邦政府开发并验证，用来研究车辆的防撞性。研究人员通过提取汽车各部件的样片数据建立有限元模型，因此该车辆模型具有较好的可信度[5]。

图1 双轴卡车有限元模型F800

F800卡车模型总质量为8.02 t，共有38 716个节点和35 035个单元，主要由4部分组成：车身部分、底盘部分、发动机和重物。其中发动机与重物采用SOLID164实体单元，赋予各向同性弹性材料模型*MAT_ELASTIC；车身和底盘的金属部件则采用SHELL163壳单元模拟，赋予分段线性塑性模型*MAT_PIECEWISE_LINEAR_PLASTIC。此外，还用到*MAT_RIGID和*MAT_SPRING_ELASTIC等材料模型。各个独立汽车部件之间的连接，例如货厢与纵梁间，通过“焊点”来模拟。当撞击作用下某些焊点的伸张力和扭曲力达到失效极限时，即产生断裂，模拟真实撞击中的部件断裂和脱离[6]。

关于车辆模型的质量与车速。根据2004年国家标准《道路车辆外廊尺寸、轴荷及质量限值》(GB1589—2004)和2000年交通部第2号令《超限运输车辆行驶公路管理规定》，比较车辆总轴重限载与车货总重限载，取两者之中的最小值为判别标准：双联轴(每侧各一单轮胎、双轮胎)载质量最大为14 t。本模型总质量为8 t。而根据高速公路相关车速规定，最低车速不得低于60 km/h，最高车速不得高于120 km/h。为了使结果更具有可对比性，选取车速分别为60 km/h、70 km/h和80 km/h三种情况，在每种情况下考虑车辆载重分别为8、10、12 t和14 t，建立仿真模型并计算，得到撞击力时程。

2.2 桥墩模型

桥墩尺寸参考“时速350 km客运专线铁路桥墩通用图”《叁桥通(2006)4308》双线圆端形桥墩[7]，见图2。该桥墩为客运专线用桥墩，圆端中心距离长7.6 m，墩宽3 m，墩高8 m。采用C30混凝土，纵筋采用HRB335钢筋。

钢筋混凝土结构的有限元模型主要有3种方式：分离式、组合式和整体式[8]。分离式模型把钢筋和混凝土作为不同的单元来处理，它的优点是可考虑混凝土和钢筋之间的粘结和滑移；整体式模型也称分布式模型或弥散钢筋模型，即将钢筋连续均匀分布于整个单元中，它综合了混凝土和钢筋对刚度的贡献。对于实际钢筋混凝土结构，即使结构构件多且钢筋布置复杂，整体式模型也足够精确。分析中采用的模型为整体式模型，如图3所示。

图2 双线圆端形桥墩(单位：cm)

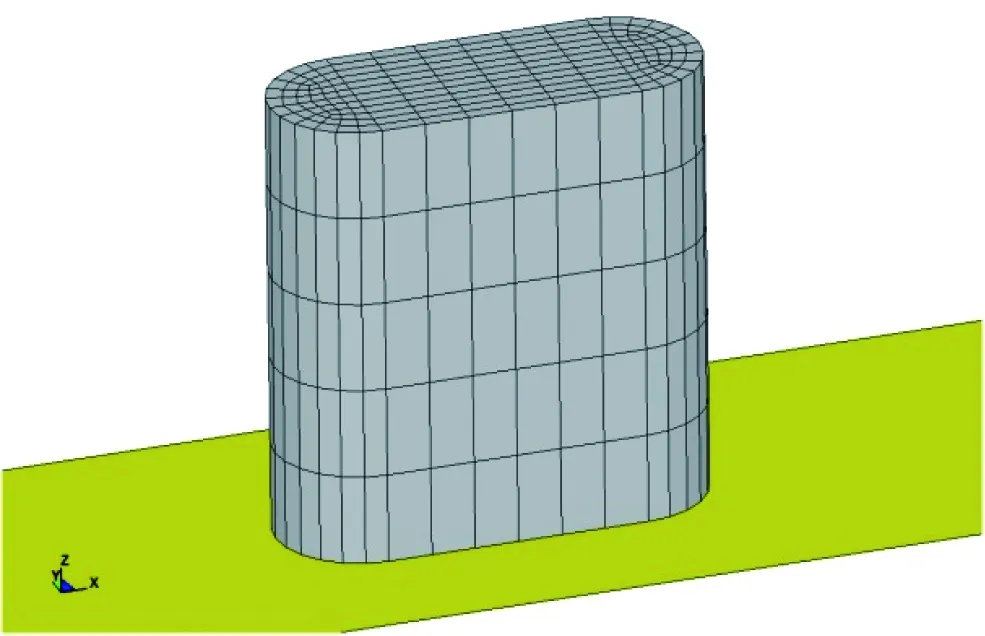
图3 双线圆端形桥墩有限元模型

为了更好地模拟撞击，桥墩采用实体单元SOLID164。关于材料模型，LS-DYNA动力分析中混凝土材料常常采用HJC本构和Brittle_damage本构。HJC本构能够模拟大应变、高应变率以及高围压下混凝土的力学行为；相比较而言，Brittle_damage本构基于损伤力学理论，能够模拟混凝土拉伸断裂行为。文献[9]在落锤实验基础上对比2种本构，结果表明HJC模型计算碰撞持续时间只有试验结果的40%左右，碰撞力峰值则明显大于试验结果。相应的Brittle_damage模型计算的碰撞力时程与试验结果吻合最好。因此，本文采用材料模型Brittle_damage本构模型进行分析，桥墩材料参数如表1所示。

表1 桥墩的材料参数

表1中，ρ为混凝土密度；E为混凝土的弹性模量；ν为泊松比；ft为初始抗拉极限；fs为抗剪极限；Gf为断裂韧度；βs为剪切保持力；η为体积黏性。另外，定义Brittle_damage材料时还需要输入钢筋混凝土的钢筋率、钢筋屈服强度和钢筋硬化模量等，在此不一一列举。

2.3 撞击力的生成和提取

本模型采用面-面自动接触(ASTS)。在碰撞过程中，车身与桥墩之间、车身的主要部件之间会发生接触，有些部件变形后会碰到其他部件，尤其是车头部分在撞击过程中会挤压到一起。这些相互挤压的部分会有力地作用，在LS-DYNA中通过定义接触来模拟它们之间力的关系。没有定义接触就无法实现撞击并生成撞击力，体现在模型中则是车辆穿墩而过。LS-DYNA提供了方便、快捷的撞击力生成命令语句*DATABASE_RCFORC，其作用是记录各个单元上的接触力，同时自动求和得到撞击力的合力。因此只需要在关键字文件中输入相应参数，通过ASCⅡ选项卡即可提取撞击力时程曲线。

3 仿真试验与结果分析

在3种车速下分别选取车辆载重为8、10、12、14 t 4种情况进行仿真分析，分别建立有限元模型并计算。4种载重通过增减车辆模型中重物的质量得到，车辆其他3部分的质量保持不变。在这4种情况中重物占总重的比例分别为35%、48%、57%和63%。

3.1 撞击力时程分析

图4为80 km/h情况下载重8 t的车辆撞击力时程曲线。撞击力作用于桥墩的时间从出现到消失共持续了约0.3 s，其时程大致可划分为突变期和平稳期；撞击力在突变期出现2次峰值，分别位于t=0.029 s时刻和t=0.054 s时刻，桥墩收到的撞击力最大值达到6.14 MN；在2个波峰过后，撞击力经过了时长约为0.084 s的持续平稳期，此过程中桥墩处于1 MN左右大小的持续波动力作用中；平稳期过后，撞击力逐渐衰减为0。

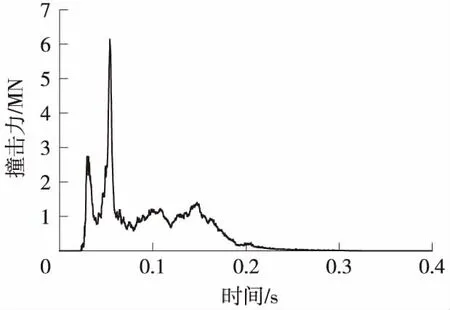
图4 载重8 t车辆撞击力时程

图5 载重8 t车辆撞击示意(80 km/h)

图5以载重8 t车辆撞击为例，给出了峰值时刻对应的撞击示意图。由几个时间点的车辆变形可以看出第一次波峰出现在车辆与桥墩接触不久后；随后内车头前部壳单元被压缩，内部发动机等实体单元与壳单元一起被压缩，并在0.054 s时第2次出现峰值；与平稳期对应的时间里，车头的壳单元和实体单元持续被压缩，直至最终车辆与桥墩脱离。

3.2 仿真结果正确性检验

判断仿真数据是否正确一般通过实验或者工程数据对比得出，而对于仿真建模计算本身正确性还可以从能量角度评价，能量守恒是判断仿真结果本身是否合理的一个标准。由于显示分析中采用缩减积分造成单元零能模式以及接触面的能量耗散，会出现沙漏能和滑移能。因此有总能=内能+动能+滑移能+沙漏能，沙漏能和滑移能一般不应超过内能的10%[10]。此处仅选取载重8 t时能量变化进行检验。能量变化时程如图6所示。

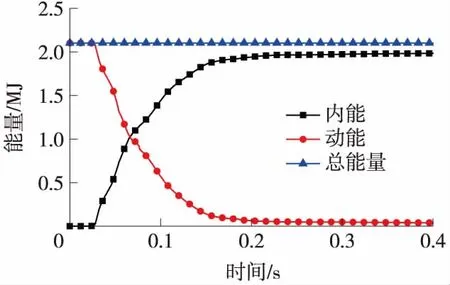
图6 能量变化时程

撞击过程的能量变化直接通过软件从计算结果中提取，其中t=0.35 s时总能量为2.101×106J，动能为0.043×106J，内能为1.979×106J，因此可知沙漏能与滑移能总和为0.079×106J，低于内能的10%。可见仿真计算的结果是可靠的。

3.3 不同载重的影响

在我国，车辆超载是一个非常普遍的现象，一旦与桥墩相撞，其影响是非常严重的。为了比较这种影响，图7(a)～7(c)分别给出了3种车速情况下不同载重车辆撞击力时程的结果对比。可以看出，突变期撞击力峰值主要受车速影响，与车辆载重无关；而在平稳期，随着载重提高和重物所占比例上升，平稳期曲线逐渐向上升起，撞击力持续时间延长，并且形成新的波峰。

美国AASHTO 2007年颁布的《LRFD bridge design specification， 4th edition》[11]中规定：位于距道路边缘9 m以内或距铁路轨道中心线15 m的桥梁墩台，未安装防护装置时，设计时应考虑1 800 kN的车辆撞击力。另外，我国《铁路桥梁检定规范》(铁运函[2004]120号)[12]中规定，对遭受汽车撞击而无防撞措施的桥梁墩台，应检算汽车撞击状态，顺汽车行驶方向的撞击力应采用1 000 kN。可见规范(特别是我国规范)提出的汽车撞击力校验值偏小，仅适用于低车速低载重的情况。

3.4 不同角度的影响(图8)

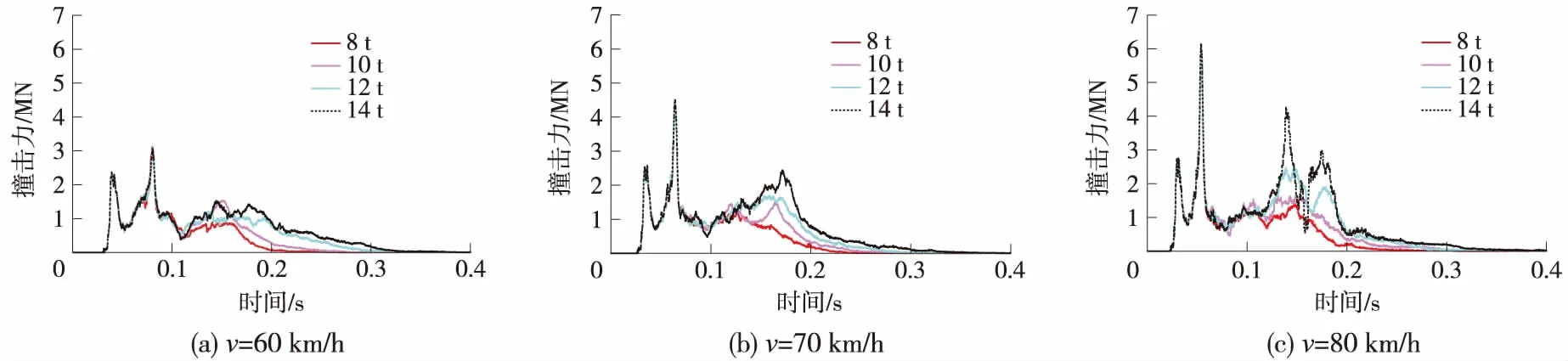
图7 不同载重车辆撞击力时程

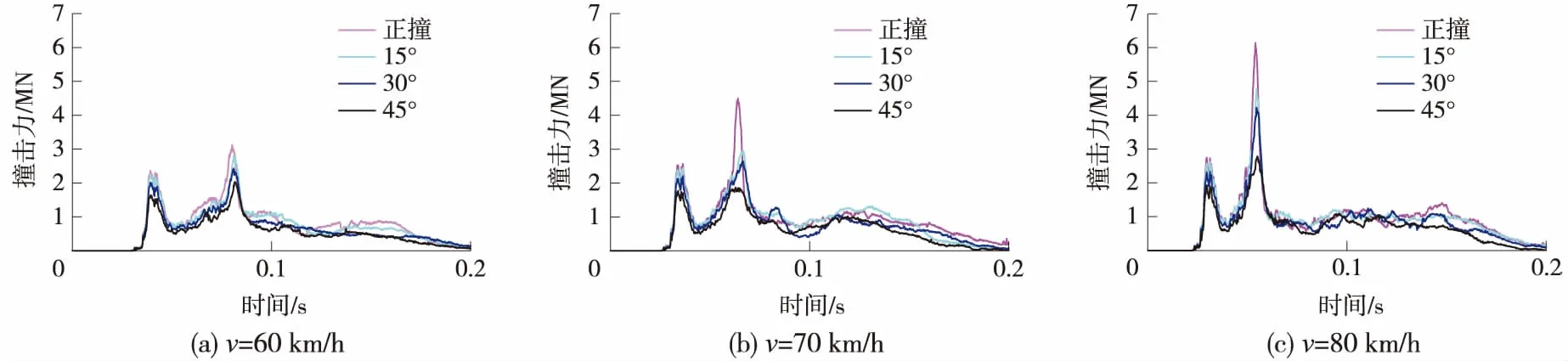
图8 不同角度下撞击力时程

实际的桥墩撞击事故中，正面碰撞很少发生，车辆常常以一定角度撞向桥墩，因此不同角度下车辆对桥墩的撞击力具有研究意义。以过桥墩圆端圆心的铅垂线作为旋转轴线，基于3种车速考虑载重8 t车辆分别以15°、30°和45°撞击桥墩。通过撞击力时程曲线可以看到，随着角度的增大，突变期和平稳期撞击力均有不同程度的下降。其中平稳期撞击力的变化较小，突变期峰值的变化幅值较大。

4 结论

基于LS-DYNA有限元仿真，得到3种车速下不同载重车辆撞击下车辆与桥墩的撞击力时程，通过对有限元计算结果的对比得到以下结论。

(1)车辆撞击桥墩时，撞击力时程可划分为突变期和平稳期。由于车头和地盘部分刚刚撞击桥墩，材料的压缩、变形并不大，突变期的撞击力呈现为双峰值形式。随着车 头部件压缩吸能，撞击力进入平稳期，持续处于较低水平。

(2)突变期撞击力主要受到车速和撞击角度的影响，车速越大，撞击角度越小，突变期峰值越大，反之越小。然而随着载重提高、重物占总重比例增加，撞击力作用总时间延长，在平稳期出现新的峰值。此外车速越高，提高载重对平稳期撞击力的影响就越大。

(3)规范提供的撞击力校验值偏小，适用于低车速低载重的情况。

[1] Thilakarathna H M I， Thambiratnam D P， Dhanasekar M， Perea N. Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment [J]. International Journal of Impact Engineering， 2010，37(11):1100-1112.

[2] Tsang H H， Lam N. College of reinforced concrete column by vehicle impact [J]. Computer-Aided Civil and Infrastructure Engineering， 2008，23(6):427-436.

[3] Liu X J， Yang J K， La Vsund P. A study of influences of vehicle speed and front structure on pedestrian impact responses using mathematical models[J]. Traffic Injury Prevention， 2002，3(1):31-42.

[4] Macdonald M D， Emerson M. Vehicle impact tests on the international barrier corporation MK VⅡ sand filled safety barrier[R]. Transport and Road Research Lab， Crowthorne (United Kingdom)：1989.

[5] EI-Tawil S， Severino E， Fonseca P. Vehicle collision with bridge piers[J]. Journal of Bridge Engineering， 2005，10(3):345-353.

[6] 包宇波，胡斌.应用LS-DYNA进行汽车正面碰撞模拟分析[J].科技创新导报，2008(7):173-174.

[7] 孙树礼.高速铁路桥梁设计与实践[M].北京：中国铁道出版社，2011.

[8] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.

[9] 陆新征，何水涛，黄盛楠.超高车辆撞击桥梁上部结构研究-破坏机理、设计方法和防护对策[M].北京：中国建筑工业出版社，2011.

[10] 熊安平，胡本清，杜宜洋.用LS-DYNA仿真模拟探索船舶刚度对船桥撞击力的影响[J].高速铁路技术，2012(1):24-26，72.

[11] AASHTO I. RFD. AASHTO LRFD bridge design specifications[S]. Washington， D.C. American Association of State-Highway and Transportation Officials， 2007．

[12] 中华人民共和国铁道部.铁运函[2004]120号 铁路桥梁检定规范[S]. 北京：中国铁道出版社，2004.