砂土地震液化势的变权重二级模糊综合评判方法研究＊

田梅青

（宿迁学院 建筑工程系，江苏 宿迁223800）

0 引言

砂土液化是指饱水的粉、细砂在受到振动时瞬间承载力丧失，由固态转为液态的过程.砂土液化是地基基础的主要震害之一.1964年日本新泻地震后，砂土振动液化已成为土动力学和地震工程学领域研究的重要课题之一.目前评价砂土液化势的方法众多，国内主要采用《建筑抗震设计规范》（GB5011-2010）中的方法［1］，欧美地区多采用Seed法［2］.这些方法多是采用单一指标评价砂土液化势，而液化的影响因素很多，各因素大多都具有相当的模糊性，因而选用模糊数学方法评价砂土液化势是可行的.基于以上考虑，本文提出了砂土液化势的二级模糊综合评判模型.

1 二级模糊综合评判数学模型

模糊综合评判法是在模糊的环境中综合考虑多种因素的影响，对某些因素关于某种目的作出综合判断的方法.在一些复杂的问题和系统中，要考虑的因素很多，先将全部因素按某种属性分类，在同类因素之间进行初级评判，再利用各类因素的评判结果进行类之间的高级评判即二级评判［3］.二级模糊综合评判方法与步骤如下：

1.1 建立因素集

设一级影响因素集为：

其中任意一个一级影响因素又可包含有多个二级因素，即二级影响因素集可确立为：

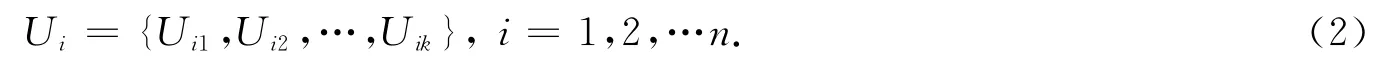
1.2 建立评价集

定义砂土地震液化势评语集为V，液化等级分成m 个级别，即

1.3 一级模糊综合评判

对每个单因素集Ui，分别作出单因素模糊综合评判，根据Ui中各因素所起作用大小确定权重集：Wi＝｛wi1，wi2，…，wik｝应满足wi1＋wi2＋…＋wik＝1.对Ui中的各因素评定出对评价集各等级的隶属度，构成k×m阶单因素评判矩阵，单因素Ui评判矩阵Ri＝｛rikj｝k×m，进行初级评判：

式中，Bi为单因素子集Ui的评判结果.

1.4 二级模糊评判

由U中各子集Ui（i＝1，2，…，n）的重要性确定类权重集W0＝｛W1，W2，…，Wn｝.以单因素模糊综合评判的结果作为评价因子，进行二级模糊综合评判，计算公式为：

式中，B为二级模糊综合评判结果.针对砂土液化势的模糊综合评判模型，其计算模型为：

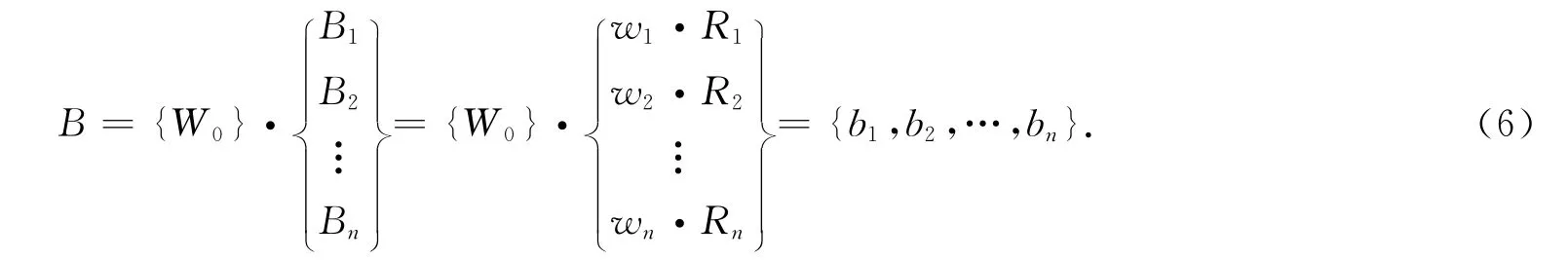
由上可见，模糊综合评判模型的建立需要解决两个关键问题，首先是选取适宜的隶属函数，建立评判矩阵；其次是各因素权重的确定.

2 建立因素集和评价集

按照上述思路，根据一些研究者的成果［4，5］，以及笔者对大量液化资料的分析总结，确定出砂土液化模糊综合评判的两级评判因子.砂土液化一级评价因子U＝｛动荷条件U1，埋藏条件U2，土质条件U3｝，二级评价因子动荷条件U1＝｛烈度U11，震中距U12，地震加速度U13｝，埋藏条件U2＝｛地下水位U21，标贯点深度U22，非液化土层的厚度U23，上覆有效应U24｝，土质条件U3＝｛标贯击数U31，平均粒径U32，粘粒含量U33｝.

评价指标的选取遵循独立、易测和重要性原则.一级评判指标共选取10个，分别对土质条件、动荷条件、埋藏条件进行初级评判，再以此评判结果作为因素进行二级评判（i＝3）.评判结果分为不液化（Ⅰ）.轻微液化（Ⅱ）、中等液化（Ⅲ）、严重液化（Ⅳ）四个等级.

3 评价因素隶属度的确定

确定模糊关系的关键是确定单因素的隶属度函数，遵循文献［6］给出的确定隶属函数的原则，考虑工程实际经验和各因素的特点，经试算，选用梯形隶属函数，如图1、图2.

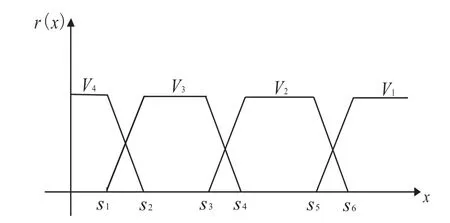
图1 第一类影响因素隶属函数曲线

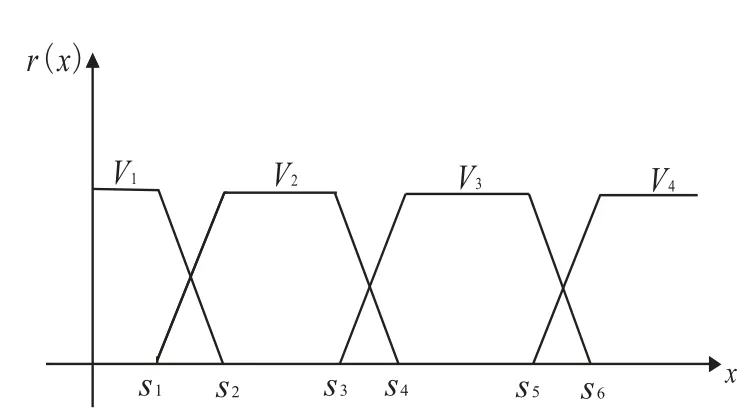
图2 第二类影响因素隶属函数曲线

砂土液化的影响因素有两类：第一类指标如震中距、平均粒径、标贯击数、粘粒含量、标贯点深度、上覆非液化土层厚度、上覆有效应力和地下水位，它们的特点是随着指标值的增大，砂土液化的可能性减小；第二类指标包括地震烈度、地震加速度，这一类指标的特点是随着指标值的增大，砂土液化的可能性增加，其中S1、S2、S3、S4、S5、S6为液化分类等级所对应区间的界限参数值，其取值如表1 所示.

4 权重的确定

砂土液化各评价指标的权重主要反映在液化势评价过程中各指标的重要程度关系，是模糊综合评判的一个关键问题.权重的确定有多种方法，最常用的如：专家打分法、层次分析法、计算反演法等.本文采用层次分析法确定权重，计算步骤如下：

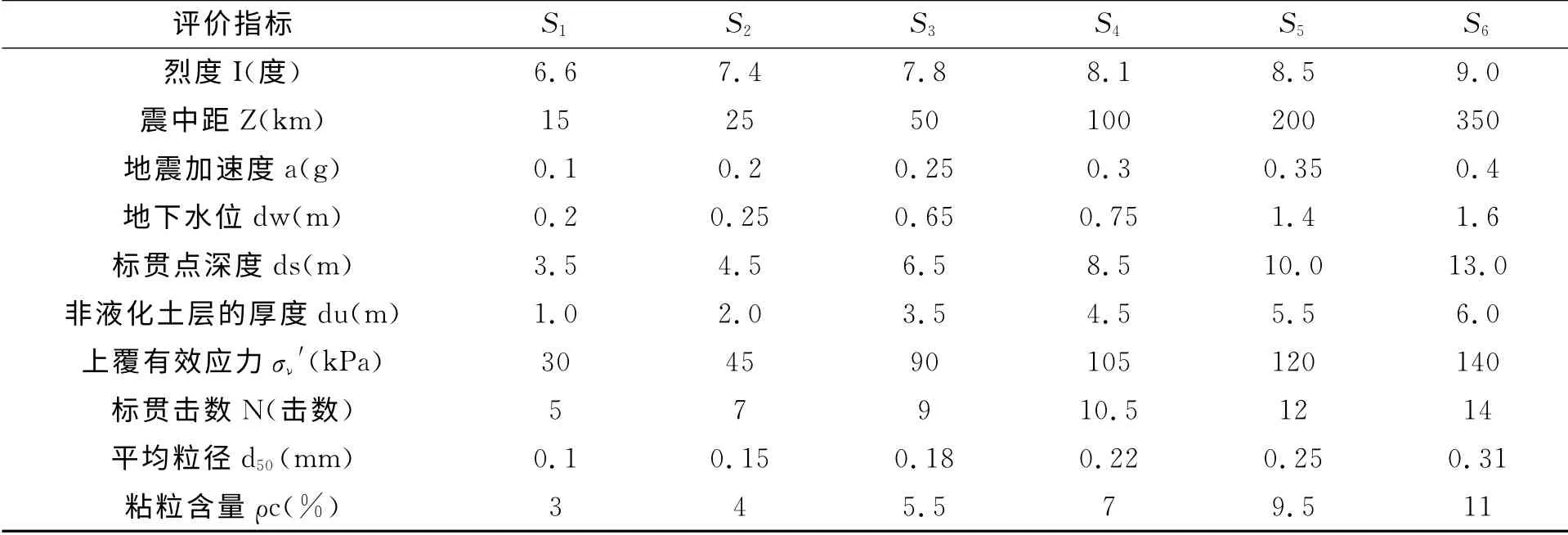
表1 砂土液化隶属函数参数取值

步骤1 比较矩阵的建立：根据砂土液化势的各个影响因子的特征及属性，将这些因子分成2个层次共10个因子，根据层次分析法中比较矩阵的构建思路和相对重要性的比较原则，通过专家打分.本文建立2个层次，4个比较矩阵，见表2～5.

表2 U 因素判断矩阵｛Ci｝（i＝1，2，3）

表3 U1因素判断矩阵｛C1j｝（j＝1，2，3）

表4 U2因素判断矩阵｛C2j｝（j＝1，2，3，4）

表5 U3 因素判断矩阵｛C3j｝（j＝1，2，3）

步骤2 权重Wi计算过程：

式中，Cij为比较矩阵元素；Wi为各评价因子权重.

此外，进行一致性验算，其计算公式为：

其中，

针对1～9阶矩阵平均一致性指标RI可由表6查得.

步骤3 由以上步骤可得本文砂土液化势二级模糊综合评判的评价因子权重，如表7，对四个评判矩阵进行一致性检验，其一致性比率CR均＜0.1，说明四个比较矩阵基本是相容的.

表6 一致性指标RI取值表

表7 评价因素权重表

步骤4 变权处理：上述方式是基于常权重的计算，而常权重是反映理想状态下评价因子和评价目标之间的相对重要程度，计算结果往往与工程实际不符.

因此，本文对以上方法确定的常权重进行变权处理，其基本思想是根据评价目标的各评价因子对砂土液化势各等级的隶属程度对其权重进行适当的放大或缩小，如果某一评价因子对砂土液化的影响程度高，则相应地将该因子的权重缩小，反之，则放大，从而确定一种动态的权重集，使评价结果与工程实际更为接近［7］.变权处理步骤如下：

求得各因素的常权重：

其中，

假设其变权重为：

其中，

按下式进行计算：

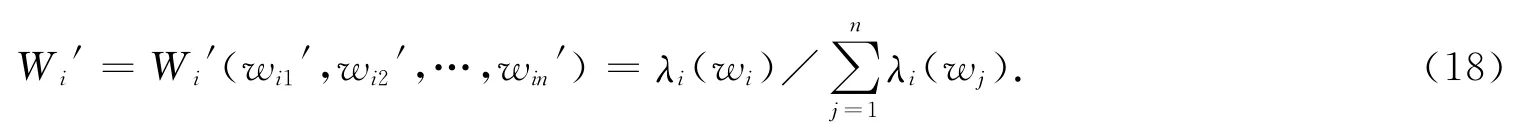
式中：i＝1，2，…，n，wi为单因素评价结果定量化处理对应的分值及评价因子的分值；λi为各因素权重wi的函数.

经以上步骤变权处理后，权重见表8.

表8 评价因素变权重

5 评判结果处理

砂土液化势评语集中评价结果有四种：不液化、轻微液化、中等液化和严重液化.而液化势的评判结果应为液化和不液化两种，本文对评判结果B＝｛b1，b2，b3，b4｝，可认为b1＋b2＞b3＋b4表示不液化，反之为液化.经此处理后，能更好地考虑液化与不液化的总偏重，使评价结果更为合理.

6 工程实例分析

为了验证砂土液化二级模糊综合评判模型的可行性，以文献［8］中列举的唐山地震液化资料为例进行计算，并将计算结果与现场液化实际情况进行比较.

从判别结果看，15组样本中，液化判别错误仅1例，远远高于《建筑抗震设计规范》砂土液化判别公式的78.3%的判别成功率（7度、8度和9度烈度区总的判别结果），对于工程而言可靠性更高.

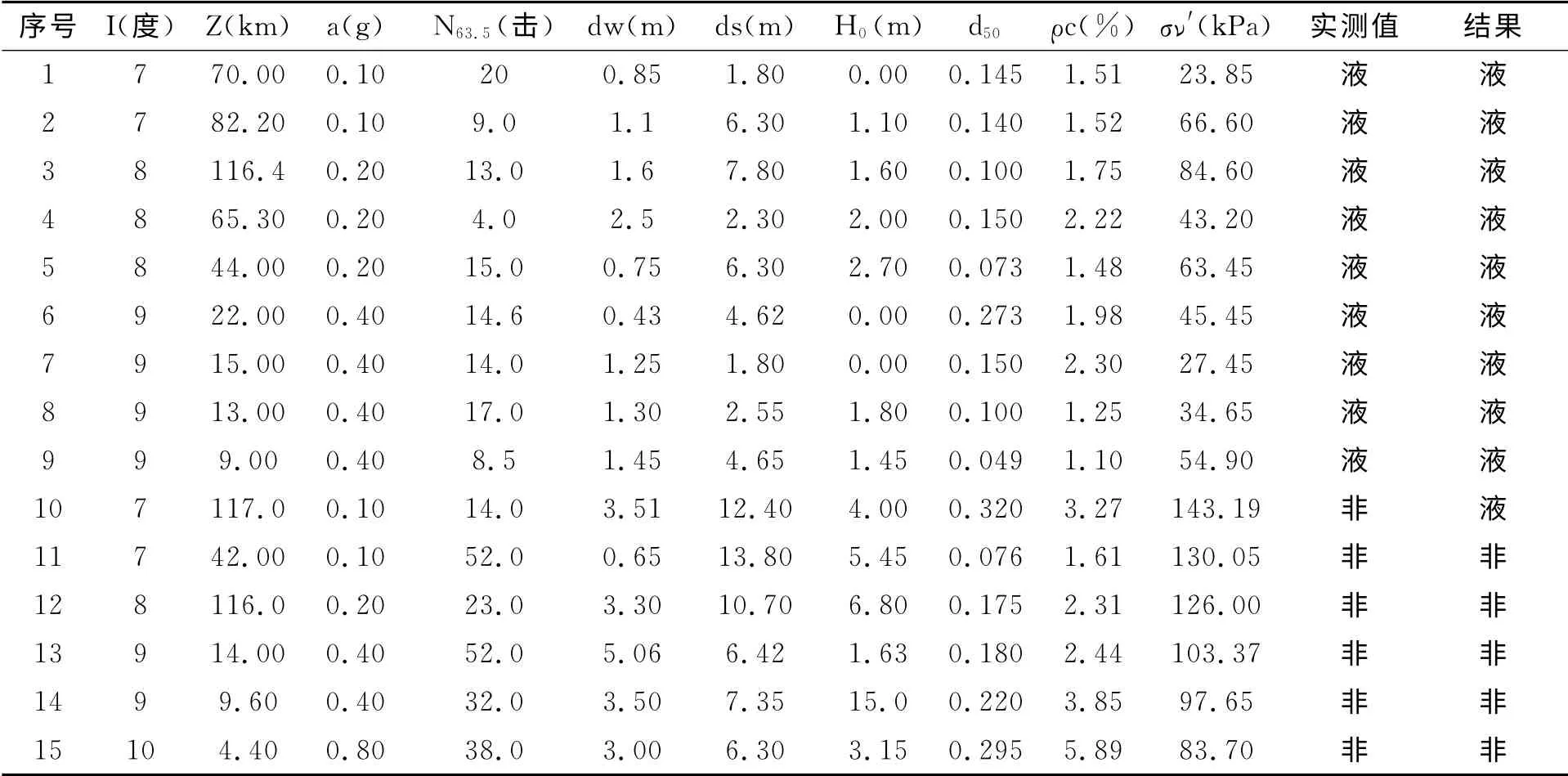
表9 地震砂土液化判别实例表

7 结语

运用二级模糊综合评判法对唐山地震实测砂土层资料进行评价，取得了满意的结果，该种方法考虑全面，与规范法相比，具有较高的判别成功率，适合于工程应用.

［1］中华人民共和国国家标准.建筑抗震设计规范（GB5011-2010）［S］.北京：中国建筑工业出版社，2010：23～26.

［2］Seed H B，Idriss I M.Simplified procedures for evaluating soil liquefaction potential［J］.JournalofSoilMechanicsandFoundationDivision，ASCE.1971，97（9）：1249～1273.

［3］刘丽.滑坡、泥石流区域危险度二级模糊综合评判初探［J］.自然灾害学报，1996，5（3）：51～59.

［4］季倩倩.砂土地震液化的模糊优化判别［J］.岩土工程技术，2001（3）：156～157.

［5］盛俭，袁晓铭.岩土震害影响因子权重研究——以砂土液化为例［J］.自然灾害学报，2012（2）：77～79.

［6］彭祖赠，孙韫玉.模糊（Fuzzy）数学及其应用［M］.武汉：武汉大学出版社，2007：163～170.

［7］程晔，曹文贵，赵明华.高速公路下伏岩溶顶板稳定性二级模糊综合评判［J］.中国公路学报，2003（4）：21～22.

［8］李方明.人工神经网络在砂土液化判别及震陷预估中的应用［D］.南京：南京工业大学，2005：30～45.