受电弓滑板与接触网导线接触电阻计算模型

陈忠华 石英龙 时 光 王智勇 康立乾

（辽宁工程技术大学电气与控制工程学院 葫芦岛 125105）

1 引言

受电弓滑板与接触网导线之间的接触区域无论如何加工、打磨以及运行过程中的相互磨损，在微观上总是呈现凹凸不平，只有少数的点实际发生了真正的接触，在这些实际接触的点中只有很少部分能够在外加机械力或击穿电压的作用下将绝缘膜破坏掉从而形成导电斑点。接触电阻的物理本质是接触电流流过导电斑点产生收缩效应引起的收缩电阻与表面膜电阻之和，接触电阻与导电斑点的形状、数目等有关。影响导电斑点的因素比较复杂，如接触元件的材料、接触形式、表面膜状况、接触力、电流大小等。接触电阻直接反映电接触性能的好坏，故接触电阻的模型及计算方法一直受到电接触学科领域内学者们的关注。

近几十年来，针对不同的具体应用，采用不同的数学方法，关于接触电阻的研究取得了一些有益的成果。文献[1]对触头静态接触电阻计算进行了分析，并提出了含膜触头接触电阻有限元计算模型。文献[2-4]提出了接触电阻的多级收缩数学模型。文献[5]在Greenwood和Williamson对收缩电阻分析的基础上进一步得到了收缩电阻起作用的区域范围，然后结合电镀层对收缩电阻的影响，针对电连接器提出了一个基于最小能量原理求具有电镀层的导体之间收缩电阻的方法。文献[6]对Greenwood提出的计算收缩电阻的数学模型进行了推广，认为Greenwood在得到收缩电阻数学模型的过程中用到的一个中间变量可以计算不同情况下（导电斑点形状不同、导电斑点间有导电膜等）的接触电阻。文献[7]研究了导电膜层（如电镀层）、污染膜层等对接触电阻的影响以及镀层不同时接触电阻的计算公式。文献[8]针对印制电路板导电胶接触问题，采用两种不同的膜电阻计算公式对M.J.Yim得到的接触电阻计算模型进行了改进。文献[9]以粗糙接触面为研究对象，提出了一个简化的多种标度粗糙度的接触电阻计算模型。文献[10]针对“T”形薄膜导电产生的收缩电阻进行计算，得到接触斑点与薄膜厚度比值为 1时，收缩电阻值最小。文献[11]通过理论分析建立了非均质导电胶接触电阻计算模型，在模型中考虑了导电颗粒接触面积、弹性变形、导电颗粒间的相互作用、边缘效应对接触电阻的影响。从现有文献来看，目前对接触电阻的研究主要针对静止接触，而针对弓网系统受电弓滑板与接触网导线之间滑动接触电阻计算模型的研究还未见有相关报道。

课题组近些年来一直从事弓网电接触方面的研究工作，对弓网滑动电接触特性已进行了较深入的研究[12,13]，在此基础上，本文通过理论分析提出了载流高速滑动接触电阻的计算模型，利用改进的高斯-牛顿迭代算法对接触电阻的计算模型进行了待定参数的求解并证明了模型的有效性。高斯-牛顿迭代算法是求解非线性回归的一种算法，目前还未见有将其应用于接触电阻模型回归分析的文献。

2 实验装置与材料

利用实验室自行研制的滑动电接触实验机进行了接触导线和受电弓滑板的载流摩擦实验。实验机固定接触导线的轮盘直径为1m。该实验机能够模拟受电弓滑板与接触网导线实际运行时的“之”字形运行轨迹；实现滑板和接触导线之间的运行速度在0～97m/s之间可调；所加载电流最大可达 800A；滑板与导线之间的接触压力可以通过改变砝码桶中的砝码来实现，使其在 0～200N之间改变。在实验过程中可以实现对滑动速度、接触电压、实际接触电流、摩擦系数等参量的实时在线测量、储存，以便于后期的数据处理。因此可以对不同接触压力、接触电流、滑动速度下的接触电阻特性进行实验研究。

滑板与接触导线间的无载流静态接触电阻和无载流滑动接触电阻利用 JL3007直流电阻测试仪测量；强电流滑动接触时的接触电阻通过接触电压和接触电流利用伏安特性间接测量，其测量方法如图1所示。

图1 滑动电接触实验机示意图Fig.1 The schematic diagram of the sliding electrical contact test machine

实验中用到浸铜碳滑板和 120mm2的铜锡合金导线，其参数见表1（温度为20℃）。

表1 滑板与导线的参数Tab.1 Parameters of the slide block and wire

3 接触电阻的实验现象及模型建立

3.1 接触电阻实验波形分析

受电弓滑板与接触网导线滑动电接触的接触电阻变化曲线如图 2所示（F=70N、v=55.6m/s、I=300A）。

图2 接触电阻随时间变化曲线Fig.2 The contact resistance variation with the time

弓网系统中摩擦副在高速滑动电接触过程中，因为接触面间的导电斑点不断产生和消失，数目在剧烈地变化着，从而使接触面积也在不断变化，致使接触电阻波动变化。通过观察发现接触电阻围绕一个中值上下波动，因此采用取其平均值来表征摩擦副间的接触电阻。从图2中可以看出在此实验条件下接触电阻围绕平均值0.064 599Ω上下波动，即滑板与接触导线的接触电阻为R=0.064 599。

3.2 接触压力对无载流静态接触电阻的影响

3.2.1 实验现象及理论分析

受电弓滑板与接触网导线无载流静态接触时，接触压力是影响二者之间接触电阻的主要因素。因此，对受电弓滑板与接触网导线之间无载流静态接触电阻随接触压力变化情况进行了测量，接触电阻随接触压力的变化曲线，如图3所示。

图3 接触电阻随接触压力的变化曲线Fig.3 The contact resistance variation with the increase of the contact pressure

从图3中可以看出，随着接触压力的增大，接触电阻逐渐减小，但当接触压力大于 120N以后，接触压力对接触电阻的影响明显变小。

理论分析：受电弓滑板与接触网导线间的接触面总是粗糙不平的，当接触压力较小时，材料产生弹性变形，此时只有很少的实际接触点，随着接触压力的增大，接触面会发生塑性变形，使实际的接触面积增大，同时接触面的空隙部分相互靠近，继续产生新的实际接触点，进而使接触电阻随接触压力的增大而减小。当总的塑性变形大到一定程度后，接触压力再增加，接触面积增大程度明显变小，接触电阻减小率也明显减小。

3.2.2 接触压力影响接触电阻的计算模型

只考虑接触压力对接触电阻影响时，得到受电弓滑板与接触网导线之间的收缩电阻为[14-16]

式中ρ——两接触材料电阻率之和（Ω·mm）；

H——浸铜碳滑板材料硬度（N·mm-2）；

n——平均导电斑点数；

F——接触压力（N）。

膜电阻为[14-16]

式中σ——导电膜的隧道电阻率（Ω·mm2）。

结合式（1）和式（2）可知，无载流静态接触时，收缩电阻和膜电阻均随接触压力的增大而减小，从而使接触电阻随接触压力的增大而减小，这与图3的变化趋势是一致的。

3.3 滑动速度对接触电阻的影响

3.3.1 实验现象及理论分析

在接触压力不变的情况下，对受电弓滑板与接触网导线之间的无载流接触电阻随滑动速度变化情况进行了测量，得到接触压力分别为 40N、60N、80N、100N，接触电阻随滑动速度的变化曲线，如图4所示。

从图4可以看出，在接触压力不变的情况下，接触电阻随着滑动速度的增大而增大。

图4 接触电阻随滑动速度的变化曲线Fig.4 The contact resistance variation with the increase of the sliding speed

理论分析：①受电弓滑板与接触网导线在滑动过程中产生的摩擦热会使摩擦副接触区温度升高，由于电阻温度效应而使接触电阻增大。随着滑动速度的增大，单位时间内摩擦热会不断增大，进而使单位时间里摩擦副接触区吸收的热量大于放出的热量，温度也会随之不断增大，进而使接触电阻不断增大；②受电弓滑板与接触网导线在滑动过程中，接触线上初始接触点上的氧化膜层会因滑动作用被擦除，使膜电阻减小。但是，温度对接触电阻的影响大于机械擦拭作用对接触电阻的影响。因此，在接触压力不变的情况下，接触电阻随着滑动速度的升高逐渐增大。由于浸铜碳滑板的热导率远远小于铜锡合金导线的热导率，因此，温度对接触电阻的影响主要是对浸铜碳滑板收缩电阻的影响。

3.3.2 滑动速度影响接触电阻的计算模型

由于滑动速度会影响接触电阻的大小，所以需对式（1）和式（2）进行修正。

在没有接触电流的纯机械摩擦下，使受电弓滑板接触点温度迅速升高的热源为摩擦热。假设受电弓滑板与接触网导线之间的摩擦功全部转化为热量被摩擦副吸收。那么，根据 Archard提出的点接触时温升的计算方法得出由纯机械摩擦时产生的热量使接触区域产生的温升为[19]

式中ζ——为经验系数，其值与滑板的材料有关；

λ——浸铜碳滑板材料热导率（W/mm·℃）；

μ——摩擦系数；

v——滑动速度（m/s）。

考虑到在实验条件下，纯机械摩擦下接触点的温升不会使接触点的温度超过摩擦副中主要导电材料金属铜的熔点1 083℃，因此，根据式（3）估算出ζ范围为ζ∈(0, 0.05)。

受电弓滑板与接触网导线之间收缩电阻将随接触部位温度的升高按1+2αθ/3变化[15,20]，则滑动时收缩电阻用式（4）进行计算

3.4 接触电流对接触电阻的影响

3.4.1 实验现象及理论分析

在接触压力和滑动速度不变的条件下，受电弓滑板与接触网导线之间的接触电阻随接触电流的变化而变化。通过实验得到接触压力为80N，滑动速度分别为 13.9m/s、27.8m/s、41.7m/s、55.6m/s，接触电阻随接触电流的变化曲线，如图5所示。

图5 接触电阻随接触电流的变化曲线Fig.5 The contact resistance variation with the increase of the contact current

从图5中可以看出，在接触压力和滑动速度一定的情况下，接触电阻随接触电流的增大呈现出减小的变化趋势。

理论分析：在接触压力、滑动速度不变的情况下，随着接触电流的增大，接触面间的焦耳热会增大，一方面大量焦耳热使摩擦副接触面材料硬度降低，接触面积增大；另一方面，电阻率也会增大，但是，接触面间因为接触点软化而使接触面积增大进而使接触电阻减小的趋势大于因为电阻率增大使接触电阻增大的趋势，从而使接触电阻随接触电流的增大而减小。

3.4.2 接触电流影响接触电阻的计算模型

在载流滑动接触条件下，由于接触电流的存在，既有焦耳热使接触面积增大，接触电阻减小的趋势；又有电阻率增大使接触电阻增大的趋势，同时还有机械因素与电气因素耦合作用对接触电阻造成的附加影响。考虑到电流对接触电阻的影响比较复杂，引入一个代表强电流滑动接触下的总接触电阻和纯机械摩擦下的接触电阻比值的参数β，即强电流滑动接触下的接触电阻为

β与接触电流之间的关系曲线如图 6所示。从图6中可以发现在不同的实验条件下，随着接触电流的增大，β逐渐减小，β随接触电流I近似成幂函数关系，如图中虚线所示。不同实验条件下的β曲线差异较小，表明接触压力和滑动速度对β的影响不是很明显，而接触电流对β的影响非常显著。因此，忽略掉接触压力和滑动速度对β的影响。

图6 β 随电流的变化曲线Fig.6 β variation with the contact current

结合图6做如式（10）所示关系假设

式中，a、b、c为经验系数，I＞100A。

根据三种不同实验条件下得到的三条β曲线确定a=248.288 917 904 508、b=-0.670 377 180 292 522、c=-1.037 563 299 151 45，其拟合效果如图6中虚线所示。在此基础上综合考虑不同实验条件下电流对β的影响，确定a、b、c三个参数的范围为a∈(200,

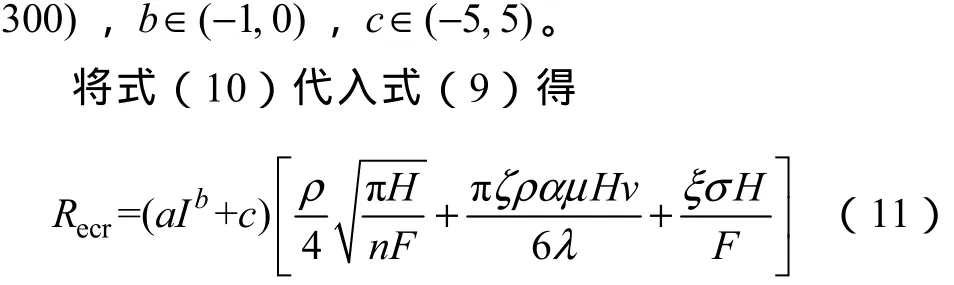
3.5 模型参数的确定

为了使求解模型参数的实验数据具有代表性，本次实验采取在三因素四水平实验条件下按照正交实验表L16（43）进行实验，见表2。为了更好地对接触电阻计算模型进行非线性拟合，将16个不同实验条件下的交叉实验重复进行三次，从而得到 48个实验数据。

表2 实验条件Tab.2 The experimental conditions

3.5.1 非线性回归模型

非线性回归模型可以表示为

式中f——期望函数；

xn——第n个相应回归矢量或自变量矢量；

φ——未知参数。

当分析一个特定的非线性回归模型时，可以认为矢量xn（n=1, …,N）是固定的，考虑期望响应关于φ的相依关系。构造N维矢量η(φ)，其中第n个分量为

假定Z服从球形正态分布，且E(Z)=0，Var(Z)=E[ZZT]=σ2。

3.5.2 基于遗传算法的高斯-牛顿迭代算法

高斯-牛顿迭代算法的运算步骤如下：

（4）用ˆ(1)代 替步骤一中的ˆ(0)， 重 复 这一过程，直至收敛。

由于高斯-牛顿迭代算法局部寻解能力强、运算速度快，但同时对初始值的依赖性强，若初始值选取不当，则可能陷入局部最优，甚至迭代过程不收敛。而遗传算法具有较强的全局寻优能力，而且对于初始值没有过多的要求，但寻优精度受到编码精度和进化代数的明显影响，局部寻优能力弱。于是，结合遗传算法和高斯-牛顿迭代算法各自的优点，把遗传算法获得的粗略解作为高斯-牛顿迭代算法的初始值，从而避免陷入局部最优，而且加强了局部寻优能力。取3组48个实验值，进行非线性拟合测试。基于遗传算法的高斯-牛顿迭代算法（GA＆G-N）、高斯-牛顿迭代算法（G-N）和遗传算法（GA），参数的范围均为：n∈ [ 3 , 20]，a∈ ( 200,300)，b∈(-1 ,0)，c∈(-5 ,5)，ζ∈ ( 0,0.05)，ξ∈ ( 0,1)；遗传算法部分的种群为50，交叉和变异概率分别为0.85和 0.1，进化 100代；高斯-牛顿迭代算法采用随机初始值。每种算法独立运行10次，其相关系数的平均值和均方差见表3。

表3 相关系数的平均值和均方差Tab.3 The average value and mean square deviation of the correlation coefficient

3.5.3 接触电阻计算模型参数

平均导电斑点数：n=19.99；经验系数ζ=0.000 039 4，a=200，b=-0.699，c=4.78；修正系数：ξ=0.99。

4 接触电阻计算模型评估和验证

在找到参数的最优解后，对非线性模型进行评估和验证是十分必要的。

4.1 学生化残差分析

定义学生化残差为

式中ˆn——第n个残差；

s——标准差；

hnn——矩阵H的第n个对角元素

以学生化残差为纵坐标，拟合值为横坐标的残差图如图7所示。

图7 残差图Fig.7 The residual

4.2 失拟分析

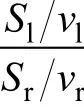
lr是否存在显著失拟。

表4 拟合数据模型的失拟分析Tab.4 The lack of fit analysis of the model of fitting data

由表4中的P值可知，模型不存在失拟。

4.3 实验验证

接触电流I=200A，接触压力分别取40N、60N、80N和 100N时，接触电阻随滑动速度变化的拟合曲线和实测值如图8所示。

接触压力F=70N，滑动速度v分别取13.9m/s、27.8m/s、41.7m/s和55.6m/s时，接触电阻随接触电流变化的拟合曲线和实测值如图9所示。

图8 接触电阻随滑动速度变化的拟合曲线和实测值Fig.8 The fitting curves of the electrical contact resistance variation with the sliding speed and the measured values

图9 接触电阻随接触电流变化的拟合曲线和实测值Fig.9 The fitting curves of the electrical contact resistance variation with the contact current and the measured values

从图8、图 9中可以看出，通过模型计算得到的结果与实验测量结果基本吻合，表明针对弓网系统受电弓滑板与接触网导线在强电流滑动接触下的接触电阻建立的计算模型具有有效性。

5 结论

（1）通过实验以及理论分析，得出受电弓滑板与接触网导线无载流静态接触时，接触电阻随着接触压力的增大而减小；无载流滑动接触且接触压力不变时，接触电阻随着滑动速度的增大而增大；强电流滑动接触且接触压力和滑动速度不变时，接触电阻随着接触电流的增大而减小。

（2）通过理论分析和参数求解得到了比较合理的针对电力机车受电弓滑板与接触网导线在强电流滑动接触下的接触电阻的计算模型，并证明了模型的有效性。

（3）改进的高斯-牛顿迭代算比高斯-牛顿迭代算和遗传算法精度更高，不但避免了陷入局部最优，而且加强了局部寻优能力。

[1] 李奎, 张冠生, 陆俭国. 含膜触头静态接触下接触电阻有限元模型及其分析[J]. 电工技术学报, 1998,13(1): 27-31.Li Kui, Zhang Guansheng, Lu Jianguo. The finite-element model and analysis for static contact resistance with film[J]. Transactions of China Electrotechnical Society, 1998, 13(1): 27-31.

[2] Willamison J B P. The microworld of the contact spot[C]. The 27th Holm Conference on Electrical Contact, 1981.

[3] Malucci Robert D. Multispot model of contacts based on surface features[C]. Proceedings of the 36th IEEE Holm Conference, 1990: 625-634.

[4] Caven R W Jr. Prediction the contact resistance distribution of electrical contacts by modeling the contact interface[C]. Proceedings of the Thirty-Seventh IEEE Holm Conference, 1991: 83-89.

[5] 丁方正. 带电镀层接触表面之间收缩电阻的计算[J].机电元件, 1990, 10(1): 7-13.Ding Fangzheng. The calculation of the contraction resistance between contact surfaces which plated electroplated layer[J]. Electromechanical Components,1990, 10(1): 7-13.

[6] Lionel Boyer. Contact resistance calculations:generalizations of greenwood’s formula including interface films[J]. IEEE Transactions on Components and Packaging Technologies, 2001, 24(1): 50-58.

[7] 堵永国, 张为军, 鲍小恒. 电接触与电接触材料[J].电工材料, 2005(4): 38-44.Du Yongguo, Zhang Weijun, Bao Xiaoheng. The electrical contact and electrical contact materials[J].Electrical Engineering Materials, 2005(4): 38-44.

[8] Aleš Duraj, Pavel Mach. Analysis and prediction of electrical contact resistance for anisotropic conductive adhesives[C]. Electronics Technology of the 31st International Spring Seminar, 2008: 358-362.

[9] Robert L Jackson, Robert D Malucci, Santosh Angadi,et al.A simplified model of multiscale electrical contact resistance and comparison to existing closed form models[C]. Proceedings of the 55th IEEE Holm Conference, 2009: 27-34.

[10] Peng Zhang, Lau Y Y, Gilgenbach R M. Minimization of thin film contact resistance[J]. Applied Physics Letters, 2010, 97(20): 204103-1-204103-3.

[11] Melida Chin, S Jack Hu. A multiple particle model for the prediction of electrical contact resistance in anisotropic conductive adhesive assemblies[J]. IEEE Transactions on Components and Packaging Technologies, 2007, 30(4): 745-753.

[12] 郭凤仪, 马同立, 陈忠华, 等. 不同载流条件下滑动电接触特性[J]. 电工技术学报, 2009, 24(12):18-23.Guo Fengyi, Ma Tongli, Chen Zhonghua, et al.Characteristics of the sliding electric contact under different currents[J]. Transactions of China Electrotechnical Society, 2009, 24(12): 18-23.

[13] 郭凤仪, 任志玲, 马同立, 等. 滑动电接触磨损过程变化的实验研究[J]. 电工技术学报, 2010, 25(10):24-29.Guo Fengyi, Ren Zhiling, Ma Tongli, et al.Experimental research on wear process variability of the sliding electric contact[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 24-29.

[14] 许良军, 芦娜, 等. 电接触理论、应用与技术[M].北京: 机械工业出版社, 2010.

[15] 程礼春. 电接触理论及应用[M]. 北京: 机械工业出版社, 1985.

[16] 吴积钦, 钱清泉. 受电弓与接触网系统电接触特性[J]. 中国铁道科学, 2008, 29(3): 106-109.Wu Jiqin,Qian Qingquan. Characteristics of the electrical contact between pantograph and overhead contact line[J]. China Railway Science, 2008, 29(3):106-109.

[17] 程礼椿, 李震彪. 接触电阻模型发展与应用[J]. 低压电器, 1993(5): 10-14.Cheng Lichun,Li Zhenbiao. The development and applications of contact resistance model[J]. Low Voltage Apparatus, 1993(5): 10-14.

[18] 吴积钦. 弓网系统电弧的产生及其影响[J]. 电气化铁道, 2008(2): 27-29.Wu Jiqin.Occurrence of arc in pantograph and overhead contact system and its interference[J].Electric Railway, 2008(2): 27-29.

[19] Bouchoucha A, Chekroud S, Paulmier D. Influence of the electrical sliding speed on friction and wear processes in an electrical contact copper-stainless steel[J]. Applied Surface Science, 2004, 223(4): 330-342.

[20] 孙明, 王其平. 温度应力对电连接器接触可靠性的影响[J]. 电工技术学报, 1990, 5(1): 34-38.Sun Ming, Wang Qiping. The effect of temperature stress on electric contact reliability of connectors[J].Transactions of China Electrotechnical Society, 1990,5(1): 34-38.