进入硅钢叠片内的漏磁通和附加损耗的模拟实验与仿真

张俊杰 李 琳 刘兰荣 范亚娜 B. Forghani 程志光

（1. 保定天威集团电工技术研究所 保定 071056 2. 华北电力大学电气与电子工程学院 北京 102206 3.加拿大Infolytica公司 蒙特利尔 H2X 4B3）

1 引言

在硅钢片内部，由于平行于叠片平面的工作磁通的交变，在硅钢片横截面内会引起涡流。但大型电力变压器中常采用的硅钢片的厚度只有 0.27～0.35mm，片间有绝缘，该部分涡流被限制在很窄的区域内，引起的涡流损耗是很小的[1]。通常在用有限元软件计算分析电力变压器涡流问题时，受计算机容量和计算时间的限制，不分析每一个叠片内的涡流，而是将变压器铁心或磁屏蔽的叠片建成一个实体块（bulk），对于叠片材料的电导率设为零或给定电导率各向异性[2,3]。对于变压器铁心和屏蔽叠片内该部分涡流损耗的计算，是待解得场后，用获得的磁通密度查比总损耗（specific total loss）曲线得到，或用斯坦梅兹公式计算得到，计算得到的损耗已经将该部分涡流损耗连同磁滞损耗计及在内。

另一方面，在电力变压器、电抗器铁心硅钢片的一部分区域涡流损耗是不能忽略的。比如在变压器的线圈端部高度，将有一部分漏磁通垂直于叠片平面穿入铁心和油箱磁屏蔽，如图1a所示。在铁心式电抗器中，每个铁心饼之间存在一个气隙，在铁心靠近气隙的边缘部分会产生磁通的边缘效应，边缘磁通（fringing flux）将部分垂直进入铁心，如图1b所示。垂直于叠片平面进入铁心和磁屏蔽的磁通引起的涡流在叠片平面内自由流动，涡流损耗是很可观的，会引起硅钢片局部过热，极端情况下会烧毁绝缘[4,5]。该类问题在实际工程中已被经验丰富的设计者找到了解决措施：对于铁心式电抗器，为避免铁心局部过热而将铁心辐射状叠积，而对于某些大容量变压器、电抗器和壳式变压器油箱磁屏蔽有采用垂直于油箱平面叠积的方式（立式），铁心的末级铁则采用高度方向开槽的方式。虽然设计者知道了采取措施的方式，但对采取的措施没有量化的目标，比如多大产品容量需要怎样的屏蔽型式，对铁心开槽的数量、高度和深度，对油箱磁屏蔽漏磁通透入的深度和屏蔽内的磁通密度分布也不是很清楚，加上垂直于油箱敷设的磁屏蔽切铁和制造工艺复杂，采取的措施都带有盲目性，需要对叠片做“单片级”（最小测量单位达到1片）的测量和分析。

图1 垂直进入叠片的磁通和引起的涡流Fig.1 Additional loss in laminated silicon sheets caused by leakage flux

2 垂直进入硅钢片的磁通和损耗的测量

用标准规定的电工钢片测试设备不能测量到由于垂直进入磁通引起的附加损耗，更不能考察“单片级”上的磁通和损耗。为此我们建立了一个叠片模型，具体做法是对国际TEAM Problem 21基准族[6]中的磁屏蔽模型P21c-M1和P21c-M2进行简化处理，即从模型中移去被屏蔽的钢板，测量随叠片层数和激励电流的增加硅钢片中铁损和与之交链磁通的变化规律，使考察“单片级”的薄层内的损耗、涡流、磁通的波形和分布的实际情况、变化规律成为可能（整体测量20片硅钢片的损耗是很难做到分离“单片级”的损耗的）。所获得的测量和计算结果、结论，将有助于合理建立有限元分析模型，验证各种工况下电磁场和损耗计算方法的有效性。

2.1 模型的结构尺寸

对国际TEAM Problem 21 基准族中的磁屏蔽模型P21c-M1和P21c-M2中移去钢板（10mm厚，普通A3钢），只保留励磁线圈和取向硅钢叠片（每片0.3mm厚，共20片）。分别简称为M1和M2模型，如图2、图3所示[7,8]，其中模型M1的硅钢片宽度为270mm，模型M2中的硅钢片分割为80mm宽的3条。硅钢片材料（30RGH120）的电磁性能数据、激励源结构设计参数，见Problem 21基准族定义[9]。

图2 模型M1和测量线圈的分布情况Fig.2 Model M1 and location of search coils

图3 模型M2和测量线圈的分布情况Fig.3 Model M2 and location of search coils

2.2 测量线圈的设置

图3示意地给出了多个测量线圈的具体位置和编号。每个测量线圈均为20匝。绕制测量线圈的导线直径为0.04mm，位置位于线圈的中心横截面上。测量线圈紧贴硅钢片绕制，可以认为测量线圈与被包绕的硅钢片之间没有气隙。

为了测定与 20硅钢片构成的叠片组所交链的总磁通（最大值），在M1和M2的另一侧线圈的中心横截面上包绕 20片叠片组设置了同样的测量线圈。

2.3 实验线路和方法

实验线路如图 4所示。其中激励电流分别为10A、15A、20A、25A（RMS,50Hz）。在每个激励电流下，屏蔽叠片从第1层、第2层、第3～4层、第5～6层、第7～10层、第11～15层、第15～20层依次增加叠片数，用日本 YOKOGAWA公司的WT3000记录测量线圈的感应电压波形数据和相应条件下的损耗数据。

根据法拉第电磁感应定律，将试验中测得的测量线圈内的瞬态电压数据（电压波形可能畸变）对时间进行积分计算，得到该测量线圈包绕的硅钢片内的瞬态交链磁通的波形数据，取其最大值，得到磁通最大值，除以该线圈内包含的硅钢片的有效面积，得到相应位置的平均磁通密度的最大值Bmax。

图4 实验线路（示意）Fig.4 Experiment system（sketch map ）

2.4 实验结果

2.4.1 叠片内的损耗

模型M1和M2在不同硅钢层数和不同的激励电流条件下损耗测量结果分别示于图5a和图5b。两个模型的损耗测量结果表明：对于10～25A施加电流，硅钢片达到4～6层片子后，硅钢片组的损耗几乎不随层数的增加而增加。这说明损耗集中在靠近漏磁方向的前4～6层片，即便前几层硅钢片内、单独放置时测量到的损耗会比20层一起放置时的损耗偏大。

M1模型和M2模型的叠片体积之比为1.125，当总层数为20层硅钢片时，测量损耗之比为17.2W/6.4W，则硅钢片中平均损耗之比约为2.4，即采用M2模拟开槽后硅钢片平均损耗降低了2.4倍。

图5 屏蔽层硅钢片不同层数时产生损耗Fig.5 Variation of measured iron loss with the number of laminated sheets at different source currents

2.4.2 测量线圈中交链的磁通

下面以25A激励电流、总层数为20层硅钢片工况为例，分析测量线圈中交链的磁通。图6给出了M1模型部分测量线圈内的交链磁通波形。

结果表明：前6层交链磁通之和占20层总的交链磁通的绝大部分，同20层的总交链磁通接近，基本上是正弦波（THD=4.7%）。对M2模型有相同的规律，且3条20层交链的总磁通之和约等于M1的20层总磁通。需要指出，在屏蔽中的磁通密度达到饱和以后，将有漏磁发生，测量线圈所交链的磁通与硅钢片中的磁通不再严格相等。

基于测量的磁通波形，进一步计算得到M1和M2模型硅钢片中的平均磁通密度波形，分别示于图7和图8。可以看出前6层硅钢片所交链的磁通不是正弦波且出现饱和。20层硅钢片中最大磁通密度随激励电流的变化情况示于图9，可以看到较大的磁通密度同样集中在前4～6层。

图6 模型M1测量线圈交链的磁通波形Fig.6 Measured flux through search coils of model M1

图7 模型M1测量线圈内的平均磁通密度波形Fig.7 Measured flux density in search coils of model M1

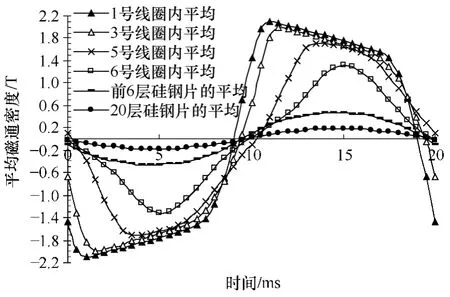
图8 模型M2测量线圈内的平均磁通密度波形Fig.8 Measured average flux density in search coils of model M2

图9 M1模型20层硅钢片中平均磁通密度峰值分布Fig.9 Variation of average flux density peak in total 20 sheets at different source currents in Model M1

图10给出了M1模型第2层硅钢片中的平均磁通密度随电流和硅钢片总层数的变化，可以看出：硅钢片增加到6层后，第2层硅钢片的磁通密度几乎不再变化。需要说明的是，第2层硅钢片单独放置时测量到的磁通密度会比 20层一起放置时的磁通密度偏大一些，但这并不能影响结论；对于10A时的曲线右侧的变化是受低漏磁影响，参见图 9，这种情况在大容量变压器中很少出现。

图10 M1模型第2层硅钢片中的平均磁通密度的变化Fig.10 Variation of measured average flux density in 2nd sheet at different source currents of model M1

3 三维有限元计算模型和结果

3.1 三维有限元模型

在交变外磁场作用下由取向硅钢片组成的叠片结构内部的三维电磁场和损耗计算是一个很具挑战性的问题，需要考虑材料的非线性和电磁各向异性，且叠片实体构件尺寸巨大但彼此绝缘的单片厚度却很小，常用厚度为0.3mm，若设叠片系数为0.97，片间绝缘的厚度只有0.3*3%=0.009mm。

基于本文建立的模型M1和M2的实验结果，在垂直进入磁通的前6层硅钢片设为三维涡流区。而 6层之外的叠片区域，计算简化为一个实体块（Bulk），设为二维涡流区，给定叠积方向上的电导率为零，即认为仅存在硅钢片的平面的涡流，硅钢片间涡流不能穿越，如图11所示。这样的假定，实际上是在有限元求解中忽略了顺延硅钢片方向的交变磁通所产生的、围绕单片流动的涡流。

图11 涡流计算模型Fig.11 Simplified lamination model

在 3D有限元分析中，考虑浅材料透入深度的影响而将上述6张硅钢片的每一片细分为3个剖分层，并且对片间绝缘进行精确的模拟。所有叠片区域考虑磁各向异性，并用正交各向异性、椭圆模型[10]和磁共轭模型[11]进行了计算对比。由于部分叠片饱和以及强非线性，采用时步有限元法(step by step timing)进行计算。

3.2 测量的磁通波形和计算的对比

当激励电流达到25A时，模型M1叠片中平均磁通的波形如图12所示。

图12 第3～4层和第5～6层中平均磁通的波形Fig.12 Flux in coil No. 3 and No. 4 with source at 25 A

计算用电磁场分析软件内MagNet®瞬态场模块求解，计算过程超过3个周波。计算和测量的磁通的波形趋于一致。

3.3 指定位置的法向漏磁的测量和计算结果

在施加10A激励电流的条件下，使用高斯计测量磁屏蔽两侧指定位置的法向磁通密度（Bx），并与相应的计算值比较，结果达到满意一致。

3.4 损耗的测量和计算的对比

分别计算出各部分硅钢片中的损耗，并分别得出了磁滞和涡流损耗，见下表。

表 不同的激励电流下的损耗Tab. Iron losses at different exciting currents

可见垂直进入硅钢片的涡流损耗在总铁损中占了“举足轻重”的份额。

4 结论

基于模型M1和M2对不同的硅钢片数量、不同的激励电流条件下对硅钢片（组）中铁损、交链磁通和空气中指定位置的法向漏磁进行了测量和计算，结果表明：

（1）垂直进入叠片平面的损耗集中在靠近漏磁方向的前 4～6层硅钢片，在硅钢片内引起的涡流损耗在总铁损中占据了“举足轻重”的份额。叠片结构部件开槽后硅钢片内损耗明显降低，且总交链磁通几乎没有改变。

（2）在磁屏蔽内部，前6层硅钢片交链磁通之和占20层总的交链磁通的绝大部分，垂直进入硅钢片的磁通呈现浅透入的特点。这一点同文献[3，4]日本学者对电抗器铁心杂散损耗的研究基本一致。

对于30RGH120硅钢片，磁通密度1.7T时的相对磁导率约等于20 000，按经典公式计算的透入深度ds约为 0.34mm，垂直入射的电磁波波长λ≈2πds=2.1mm，约等于硅钢片的7片。

（3）每一层硅钢片所交链的磁通不是正弦波，这对畸变波损耗的计算提出了要求。

（4）详细考察了叠片内铁损和交链磁通随激励电流的增加变化的情况，相应的测量和计算结果相吻合，验证了MagNet®瞬态场三维时步法计算复杂的叠片问题的有效性。

由于磁通和附加损耗的浅透入，对大型大容量变压器的铁心末级铁和磁屏蔽提出了改进要求，如需在铁心末级铁高度方向上开槽，在考虑平行于油箱表面放置的油箱磁屏蔽（“平式”）时不能一味的单靠增加磁屏蔽的厚度来妥善解决漏磁通的吸收问题。

基于磁屏蔽模型M1和M2，深入考察“单片级”的薄层内的损耗、电磁行为，将有助于建立大型、复杂外施磁场条件下叠片铁损计算的有限元模型，进一步研究、验证有效的工程分析方法。

本文分析提出了对常规“平式”磁屏蔽浅透入的担忧，而“立式”磁屏蔽则不存在浅透入的问题。此外磁屏蔽形式还有阶梯式、卷绕式等结构形式，都有待在新制作的双铁心镜像法漏磁试验装置产生的产品级漏磁场下做进一步的试验、分析和对比。

[1] 许实璋. 电机学[M]. 北京: 机械工业出版社, 1988.

[2] Oszkár Bíró, Kurt Preis, Igor Ticar. A FEM method for eddy current analysis in laminated media [J]. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2005, 24(1): 241-248.

[3] Hollaus K. Biro O, A FEM formulation to treat 3D eddy currents in laminations[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1289-1292.

[4] Nogawa S, Kuwata M, Daisuke Miyagi, et al. Study of eddy-current loss reduction by slit in reactor core[J]. IEEE Transactions on Magnetics, 2005, 41(5):2024-2027.

[5] Nogawa S, Kuwata M, Takaaki Nakau, et al. Study of modeling method of lamination of reactor core [J],IEEE Transactions on Magnetics, 2006, 42(4):1455-1458.

[6] Cheng Zhiguang, Takahashi Norio, Forghani Behzad.TEAM Problem 21 family(V.2009)[EB/OL]. (2010-03-02).[2012-08-07]. http://www.compumag.org/jsite/team.html.

[7] Cheng Z, Takahashi N, Forghan B, et al. Analysis and measurements of iron loss and interlinkage flux inside silicon steel lamination[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1222-1225.

[8] Cheng Z, Takahashi N, Forghani B, et al. Effect of excitation patterns on both iron loss and flux in solid and laminated steel configurations[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3185-3188.

[9] http://www.compumag.org/jside/html.

[10] Dedulle J M, Meunier G, Foggia A, et al. Magnetic fields in nonlinear anisotropic grain-oriented iron-sheet [J]. IEEE Transactions on Magnetics, 1990,26(2): 524-527.

[11] Silvester P P, Gupta R P. Effective computational models for anisotropic soft B-H curves [J]. IEEE Transactions on Magnetics, 1991, 27(5): 3804-3807.