高风速段次优功率追踪方式的风电调频方法
吴子双 于继来 彭喜云
(哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001)
1 引言
新颁布的《风电场接入电力系统技术规定》(GB/T 19963-2011),虽对风电机组并网运行时的频率范围进行了规范,也涉及到有功功率控制问题,但尚未明确风电机组参与系统调频。目前,国内外学者主要在风电机组有功输出对系统频率的影响[1-11]和风电功率余量调节方面进行了一定的研究[11,12],并从不同角度对风电机组的控制策略加以改进[9-11,13-19]。对 DFIG,通常可通过调节其转子转速释放或存储部分动能的方式参与系统频率调节[1];或追踪 90%次优功率曲线,并通过转速调节参与系统调频[10,11]。前者调节能力有限,且只适用于系统频率波动较快成分的调节;后者可能因整个运行区间留有较大功率余量而影响机组运行的经济性。如何兼顾机组运行的经济性和系统频率调节需求,并适应不同变化速率频率分量的调节需要,有待进一步深入研究。
本文提出一种风速分段调频策略,并兼顾机组运行经济性和调频能力需求整定机组启动参与调频的风速门槛值和追踪次优功率曲线时的上调余量。在此基础上,设计了一、二次调频控制器,并由仿真证明了新型调频方法的性能。
2 调频策略与有关定值整定方法
2.1 一、二次频率调节方式
与常规机组类似,DFIG可参与电力系统一、二次调频,但调节方式有所不同。本文调频方式如下:
(1)转速控制。该控制过程短、变化快,能快速吸收或释放转子动能以有效应对频率f波动中变化迅速的部分,这与常规机组的一次调频类似。
(2)桨距角控制。该控制属于机械过程,调节相对较慢,可用来调整f波动中变化较慢的部分。本文在一次调频中加入桨距角控制进行辅助调节,能够增强一次调频能力。除此,因为桨距角控制直接改变的是风能利用系数,它能够稳定地改变DFIG的输出功率,故应能胜任二次调频需要以进一步降低系统中因功率长期缺额或过剩造成的频差。
在通常情况下,可要求较多的 DFIG参与一次调频,其中的少量DFIG同时参与二次调频。
对参与一、二次调频或仅参与一次调频的DFIG,均涉及到机组有功余量值的合理整定问题。兼顾调频能力需求和机组经济性,应是整定有功余量需要重点考虑的因素。
2.2 有功余量整定方法
Praghnesh Bhatt等提出追踪次优功率曲线运行[11],如图1所示。设初始点为A,当系统f下降时,调节转子使转速下降以迅速释放部分动能,与此同时DFIG运行点会沿图中AB间实线向B转移,趋向最优功率曲线,输出有功功率增加,相当于有两部分能量同时参与频率调节,增强了调频能力。

图1 次优功率追踪曲线Fig.1 Suboptimal power tracking curve
此方式虽较最优功率追踪方式在调频能力上有所加强,但可能会造成不小的风能损失,且不具备进一步参与二次调频的能力。本文兼顾机组运行经济性和需要提供的调频能力,对功率追踪曲线以整定的风速门槛值为界进行分段处理,如图2所示:在低风速功率较低时,不要求其参与调频,仍然采取最大功率追踪方式;在风速较高且大于门槛值时,风电功率较高,希望其适当参与系统调频,此时采取次优功率追踪方式。分段后的风电功率曲线,其风速分段门槛值和功率次优的程度如何整定,需兼顾机组和电网需求。下面重点分析该问题。

图2 改进的次优功率追踪曲线Fig.2 Improved suboptimal power tracking curve
当电网风电达到高渗透率且因其引起系统调频资源需求额外增长幅度达到一定水平时,可要求风电逐步参与系统调频。考虑到风电享受优惠发展的特殊性,当其参与调频时,可参照电网中对常规机组调频能力的规定,本着“共同但有区别的责任”原则进行适当放宽。
设电网中常规机组调速器的调差系数整定(平均)值为Ru,则风电场一次调频的调差系数Rw为

式中,σ为风电场相对于常规机组调差系数放宽的比例系数,σ>1。
另外,我国对3 000MW以上电力系统的f偏差规定不超过±0.2Hz,因此风电机组因承担调频需要预留的有功功率余量,可以暂时参照0.2Hz的f偏差限值进行折算,即

式中,f0为系统标准频率(=50Hz);ρw为预留的有功功率余量百分比,具体应用时,可直接使用该整定值乘以机组实际功率水平获得功率余量MW值。
假设Ru典型值为 5%,当σ取 2(即同等容量下风电机组的调频容量需求只是常规机组的一半)时,Rw=10%。代入式(2)得ρw为4%。
进一步地,可将最大有功功率余量 4%按一定比例分配给一、二次调频。例如,对只参与一次调频的风电机组(场),可将其中的3%功率余量分配给由转速控制承担的一次调频部分,其余 1%分配给由桨距角控制承担的一次调频部分;对少量参与二次调频的机组(场),可将其中的1%功率余量分配给转速控制部分,其余 3%分配给桨距角控制部分。至于对实际电网,最大有功功率余量的分配,可参照由一定方法评估所得的一、二次调频需求比重进行。
上述预留的 4%功率余量是针对图 2高风速段运行时的次优功率曲线而言的。其中,高风速分段的门槛值需要在考虑允许的风电机组(场)风能损失上限值的条件下进行整定。具体方法如下:
设需整定的风电机组(场)所在区域电网全年的风电功率水平百分比(风电功率实际出力相对于区域电网风电总装机容量的百分比)的概率密度分布已知(由历史数据统计得出)。基于此概率密度和已经获得的有功功率余量ρw,以及风电损失最大允许值ψw(损失风电电能相对于全年可发总风电电能的百分比),可以先按如下步骤整定与高风速段门槛值对应的风电功率水平百分比的门槛值τw:
(1)设τw的初值τw0(接近 100%)。
(2)从区域电网风电功率水平百分比概率密度分布曲线上,在[τw0,100%]内按一定步长Δτw采样若干点的概率密度值pi,i=1~N,N为采样点数。
(3)计算在[τw0,100%]内因预留有功功率余量ρw而可能损失的风电能量百分比:

式中,M为在[0,100%]内按Δτw采样概率密度值的总点数。
整理式(3)得

(4)判断ψ<ψw? 若成立,将τw0-Δτw赋给τw0返回(2);否则,将τw0赋给τw,结束。
获得τw后按如下关系折算高风速段门槛值vw:

式中,ve为风电机组额定风速,m/s。
为防止实际控制过程因风速在vw上下变动造成风电机组(场)在参与调频(次优曲线)与不参与调频(最优曲线)之间频繁切换,影响机组寿命和控制稳定性,可将vw拓展为门槛带[vwL,vwH],当风速由高于vwH进入该带时,保持机组参与调频,只有在风速低于vwL时才退出调频功能,进入常规的最优功率追踪模式;当风速由低于vwL进入该带时,保持机组最优功率追踪模式,只有在风速高于vwH时才又进入调频模式。
图3给出了某区域电网全年风电功率水平百分比的概率密度。设某风电机组的额定风速为 12m/s时,预留的功率余量为 4%,当该区域风电损失最大允许值ψw在 0.5%~3.5%范围内变化时,整定的高风速段门槛值vw见下表所示。对ψw=3%的情况,vw=8.4m/s,若门槛带按ψw±0.5%的偏差进行设置,则[vwL,vwH]=[7.2, 9.2] m/s。

图3 区域电网全年风电功率水平百分比概率密度Fig.3 Probability density of annual wind power level percentage for regional power grid

表 高风速段门槛值Tab. Threshold value of high speed section
3 一次、二次调频控制方法
3.1 一次调频转速控制方法
一次调频转速控制逻辑如图4所示。当风速高于vwH时,DFIG运行在次优功率曲线上。一旦f变化量Δf及其变化率dΔf/dt均超出死区,DFIG将迅速释放或存储转子动能,以调节频差。在调节时转速不能过低,否则可能引发停机,故需在控制系统中设置最低转速环节(例中ωL为0.8(pu))。若f下降,且Δf和 dΔf/dt均超出死区,DFIG立即调节转子转速增加有功出力,此时转子转速下降,由于ωL限制,转速不会低于 0.8(pu),一旦f恢复到死区以内,调节结束,输出的调节信号恢复为0,DFIG转速恢复,重新开始追踪次优功率曲线。
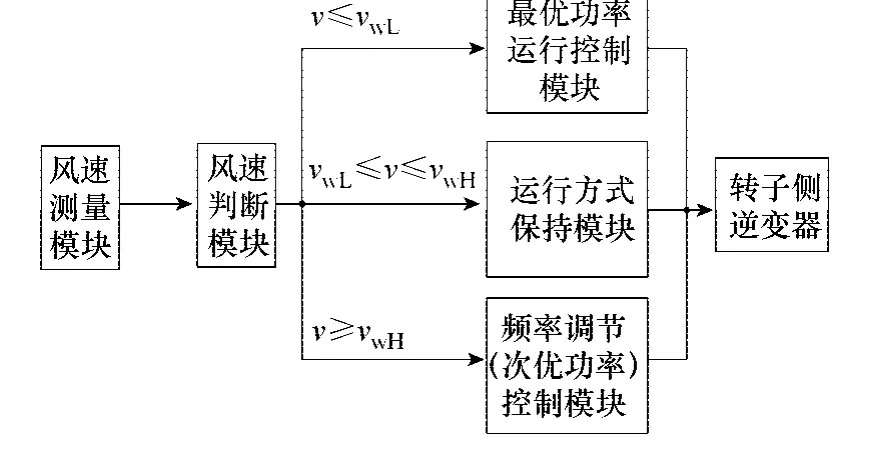
图4 转速控制方法控制逻辑Fig.4 Control logic of rotation speed control method
若风速低于vwL,DFIG追踪最优功率曲线;若处于门槛带[vwL,vwH]内,则暂时保持原控制模式。
与图4逻辑对应的控制框图如图5所示。图中,转子转速高于最低转速时,输出的逻辑值为 1,否则为0;由频率变化率超出死区输出的逻辑值1,否则为0。两个逻辑值“相与”后再与调节信号相乘,输出的非“0”信号启动转子侧逆变器PI控制器以调整转子转速。

图5 转速控制模块Fig.5 Module of rotation speed control
3.2 一次调频桨距角辅助调节控制
桨距角调节较转速调节的响应慢,通常可参与频率变化较慢分量的调节。
风力发电机组的风能捕获模型为

式中,Cp为风能捕获系数;ρ为空气密度;A为叶轮的扫风面积;v为风速;系数kp=0.5ρA。
风能捕获系数为

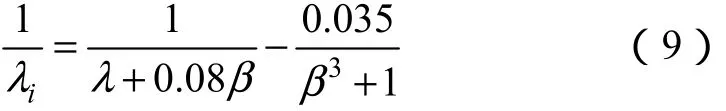
式中,λ为风力机叶尖速比;ωr为风力机转速;R为风力机叶轮半径;β为桨距角,C1~C6为常数,与具体型号的机组特性有关。
当系统出现频差Δf时,根据调差系数可以计算出风电机组需要调节的有功ΔP;再由式(6)得与ΔP对应的Cp大小、由式(7)~式(9)得β。
然而,β(Cp,λ) 为非线性隐函数,求解困难。为方便使用,可根据风电机组实际工况进行简化。
当机组追踪最优功率曲线运行时,对不同的风速,Cp和λ保持定值不变[20]。类似地,可以分析得出,当机组追踪相对于最优功率留有固定余量的次优功率曲线时,Cp和λ也保持定值不变。因此,在本文调频控制中,β成为关于Cp的单变量函数,可由简单的二次函数拟合所得,即

当针对某典型机组取式(7)中C1~C6值分别为0.517 6、116、0.45、-21和 0.006 8时,式(10)系数分别为a=-11.487 38、b=-35.184 82和c=19.200 77。桨距角控制的控制逻辑与图4类似,区别在于此时的控制信号送给桨距角控制系统。相应的控制框图如图6所示,图中F(Cp) 可以采用式(10)简单形式,当判断f变化率在较低范围内时输出逻辑1,调节量与之相乘即为ΔCp。Cpref为Cp初始值,根据 2.2节保留策略,只参与一次调频的风电机组(场),1%功率余量分配给频率一次调频(桨距角控制)部分,则相应Cpref取为0.99倍最优Cp;少量参与二次调频的风电机组(场),3%功率余量分配给桨距角控制部分,相应Cpref取为0.97倍最优Cp。

图6 桨距角控制模块Fig.6 Module of pitch angle control
3.3 二次调频控制
二次调频控制模块如图7所示。其中,给定机组功率调节量ΔP*并根据式(6)计算得到调节量ΔCp*并与Cp初始值作差,通过式(10)拟合方程得到相应桨距角值β*,即可得到目标调整功率。

图7 二次调频控制模块Fig.7 Module of the secondary frequency regulation
4 仿真分析
4.1 仿真对象
对图8系统仿真,并考察高风速和低风速工况、渗透率为5%和20%时加减负载后的调频效果。
图8系统容量为200MW,有一台水电机组,经50km线路连在110kV/35kV变压器上,变压器另一侧连接到负载母线上,两组各自连在一条母线上的风电机组,每组 10台,分别通过两台 690V/35kV变压器接到 40km线路上,最后连在负载母线上。负载分为两个,一个为恒定负载,另一个通过断路器作为突加或突减负载,水电厂调差系数5%。

图8 仿真系统图Fig.8 System for simulation
4.2 高风速突加负载
设风速为8m/s且处于门槛风速以上,系统初始负荷为150MW,在10s时突增10MW负载。
图9为风机桨距角控制曲线,桨距角初始位置在高于0°上,该值大小根据有功保留策略计算得出,在10s时,由于突加负载,桨距角迅速减小到0°,参与频率调节。

图9 高风速突加负载桨距角变化曲线Fig.9 Curve of pitch angle in the condition of high wind speed and increasing load
图10为风电场有功出力曲线。稳态时,出力分别为2.2MW和8.5MW,突加负载后,风电场迅速增加出力参与频率调节,最终根据二次调节指令有功输出分别增加0.3MW和1.2MW。

图10 高风速突加负载风电场有功出力Fig.10 Active power of wind farm in the condition of high wind speed and increasing load
图11为系统f变化曲线。在风电机组未参与系统调频时,风电渗透率越高,f下降越大,最低下降到 48.86Hz(见图 11b),而在风电机组参与系统频率调节后,风电渗透率越高f恢复越好,最终稳定在 50Hz附近。这说明,渗透率不是造成调频负担增加的原因,相反,只要风电机组适度参与调频,f质量可以维持在较高水平。

图11 高风速突加负载系统频率变化曲线Fig.11 Curve of system frequency in the condition of high wind speed and increasing load
4.3 高风速突减负载
设系统初始负荷为 150MW,在 10s时突减10MW负载。
图12为风机桨距角控制曲线,在10s时,由于突减负载,桨距角迅速调节参与调频最终运行在10°和 6°。

图12 高风速突减负载桨距角变化曲线Fig.12 Curve of pitch angle in the condition of high wind speed and reducing load
图13为风电场有功出力变化曲线。稳态时,出力分别为2.2MW和8.5MW,突减负载后,风电场迅速减少出力参与频率调节,最终在二次调频作用下,在一段时间后出力分别下降约0.3MW和1.2MW。

图13 高风速突减负载风电场有功出力Fig.13 Active power of wind farm in the condition of high wind speed and reducing load
图14为f变化曲线。在风电机组未参与系统调频时,风电渗透率越高,f上升越大,最高上升为51.1Hz(见图14b),而在风电机组参与f调节后,f最高上升值均有所下降,并且风电渗透率越高,下降越明显,最终稳定在50Hz附近。
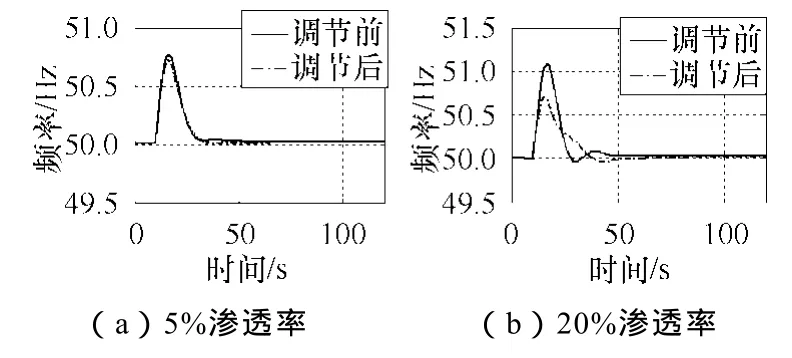
图14 高风速突减负载系统频率变化曲线Fig.14 Curve of system frequency in the condition of high wind speed and reducing load
4.4 低风速突加负载
设风速为6m/s且处于门槛风速以下,系统初始负荷为150MW,在10s时突增10MW负载。
在本文策略中,风速低于门槛值时,风电机组(场)不参与调频。为说明低风速不参与调频的负面影响,可反过来先考察低风速时参与调频的正面效果。若正面效果不明显,则可以认为低风速不参与调频的负面影响较小,从而间接地说明低风速不参与调频的合理性。
下面给出低风速时参与调频的仿真效果。
图15为风机桨距角控制曲线,在10s突加负载,桨距角迅速减小到0°,参与频率调节。

图15 低风速突加负载桨距角变化曲线Fig.15 Curve of pitch angle in the condition of low wind speed and increasing load
图16为风电场有功出力曲线。突加负载后,风电场迅速增加出力参与频率调节,但调节功率较高风速时明显降低。
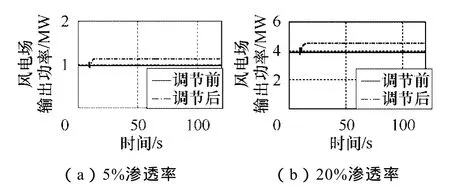
图16 低风速突加负载风电场有功出力Fig.16 Active power of wind farm in the condition of low wind speed and increasing load
图17为f变化曲线。在各渗透率情况下,频率调节效果均不明显。这说明,在低风速段,可以允许风电机组(场)不参与电网调频。
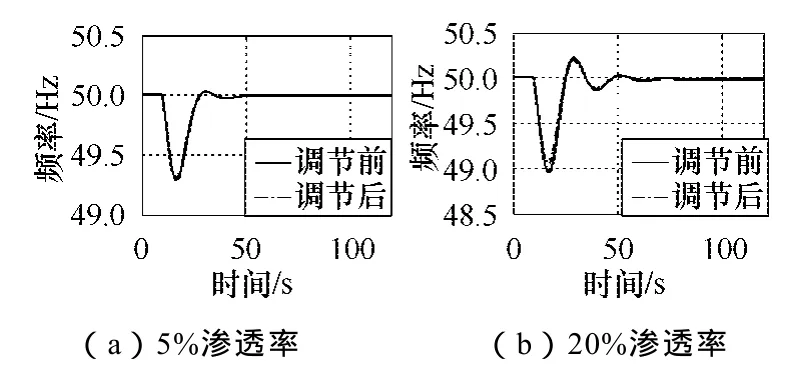
图17 低风速突加负载系统频率变化曲线Fig.17 Curve of system frequency in the condition of low wind speed and increasing load
4.5 低风速突减负载
反过来考察低风速参与调频的正面效果,以间接说明低风速不参与调频的合理性。
系统在10s时突减10MW负载,图18为风机桨距角控制曲线,可以看到在10s时,由于突减负载,桨距角迅速调节至10°减小出力。
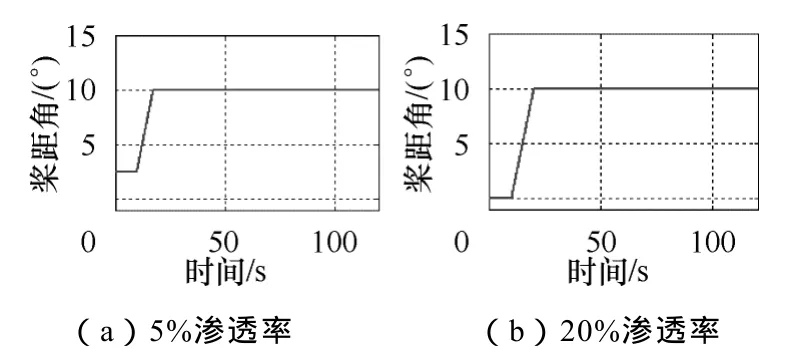
图18 低风速突减负载桨距角变化曲线Fig.18 Curve of pitch angle in the condition of low wind speed and reducing load
图19为风电场有功出力变化曲线。由于本身出力较小,风电场在调节过程中有功出力减小量也较高风速时明显减小。
图20为f变化曲线。在各渗透率情况下,低风速段不参与调频相对于参与调频,差异不明显。

图19 低风速突减负载风电场有功出力Fig.19 Active power of wind farm in the condition of low wind speed and reducing load

图20 低风速突减负载系统频率变化曲线Fig.20 Curve of system frequency in the condition of low wind speed and reducing load
综上所述,在低风速段,特别是渗透率不高时,风电机组(场)参与调频,有一定效果,但并不明显,此时可以允许其不参与调频(本文策略);当渗透率较高且处于高风速段时,要求风电机组(场)适当参与调频,可以减轻其他常规机组调频的压力,而自身经济损失不大,可以限制在百分之几以内。
5 结论
在高风速段追踪次优功率、并采用转速和桨距角控制的合理配合,使 DFIG参与系统调频,具有兼顾机组运行经济性和系统调频需求的特性;风电渗透率越高,系统在负荷变化时频率偏离越明显,而加入新策略后,系统调频能力明显增强。
多种条件下的仿真计算结果表明,高风速段次优功率追踪方式的风电机组调频方法,是可行的,对今后具体设计风电机组控制系统具有参考价值。
[1] 邹贤求. 变速恒频风电机组参与一次调频的控制方法研究[D]. 湖南: 湖南大学, 2010.
[2] 韩小琪, 宋璇坤, 李冰寒, 等. 风电出力变化对系统调频的影响[J]. 中国电力, 2010, 43(6): 26-29.Han Xiaoqi, Song Xuankun, Li Hanbing, et al.Study of impact of wind power variable output on frequency regulation[J]. Electric Power, 2010, 43(6): 26-29.
[3] 石一辉, 张毅威, 闵勇, 等. 并网运行风电场有功功率控制研究综述[J]. 中国电力, 2010, 43(6): 10-15.Shi Yihui, Zhang Yiwei, Min Yong, et al.Review on active power control researches of a grid-connected wind farm[J]. Electric Power, 2010, 43(6): 10-15.
[4] 朱卫平, 王秀丽, 王锡凡. 分频风力发电系统最优功率输出控制[J]. 电力自动化设备, 2010, 30(6): 6-10.Zhu Weiping, Wang Xiuli, Wang Xifan, et al.Optimal power output control of fractional frequency wind-power generation system[J]. Electric Power Automation Equipment, 2010, 30(6): 6-10.
[5] 陈宁, 于继来. 兼顾系统调频需求的分布式风电分散自治调控策略[J]. 电工技术学报, 2008, 23(11):123-130.Chen Ning, Yu Jilai. Strategy for decentralized autonomous regulation of distributed wind power considering system frequency regulation demand[J].Transactions of China Electrotechnical Society, 2008,23(11): 123-130.
[6] 乔颖, 鲁宗相. 考虑电网约束的风电场自动有功控制[J]. 电力系统自动化, 2009, 33(22): 88-93.Qiao Ying, Lu Zongxiang.Wind farms active power control considering constraints of power grids[J].Automation of Electric Power Systems, 2009, 33(22):88-93.
[7] 韩民晓, 崔立军, 姚蜀军, 等. 大量风电引入电网时的频率控制特性[J]. 电力系统自动化, 2008,32(1): 29-33.Han Minxiao, Cui Lijun, Yao Shujun, et al.Frequency control characteristics for a power system with large amounts of wind power[J]. Automation of Electric Power Systems, 2008, 32(1): 29-33.
[8] 薛迎成, 邰能灵, 宋凯, 等. 变速风力发电机提供调频备用容量的研究[J]. 电力自动化设备, 2010,30(8): 75-80.Xue Yingcheng, Tai Nengling, Song Kai, et al.Variable-speed wind turbines provide primary reserve for frequency control[J]. Electric Power Automation Equipment, 2010, 30(8): 75-80.
[9] 尹向前. 变速恒频双馈风电机组控制策略研究[D].天津: 天津理工大学, 2008.
[10] De Almeida, Rogério G, Peças Lopes J A.Participation of doubly fed induction wind generators in system frequency regulation[J]. IEEE Transactions on Power Systems, 2007, 22(3): 944-950.
[11] Praghnesh Bhatt, Ranjit Roy, Ghoshal S P. Dynamic active power support by doubly fed induction generator for frequency control[C]. IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, June 14-17,2010: 131-136.
[12] De Almeida, RogérioG, Peças Lopes J A. Optimum generation control in wind parks when carrying out system operator requests[J]. IEEE Transactions on Power Systems , 2006, 21(2): 718-725.
[13] 张海龙, 曾宁春, 付强. 基于变速恒频的风力发电机控制系统研究[J]. 电力科学与工程, 2010, 26(12):1-3.Zhang Hailong, Zeng Chunning, Fu Qiang. Study on wind power generation control systems based on variable speed constant frequency[J]. Electric Power Science and Engineering, 2010, 26(12): 1-3.
[14] 王兴武, 张照彦, 武永利. 变速恒频双馈异步风力发电机建模与仿真研究[J]. 计算机仿真, 2009,26(10): 294-306.Wang Xingwu, Zhang Zhaoyan, Wu Yongli. Modeling and simulation of variable-speed constant-frequency double-fed wind generator[J]. Computer Simulation,2009, 26(10): 294-306.
[15] 王斌, 吴炎, 丁虹, 等. 变速变桨距风电机组的高风速变桨距控制[J]. 电力自动化设备, 2010, 30(8):81-83.Wang Bin, Wu Yan, Ding Hong, et al. Variable-pitch control of wind turbine at high wind speed[J]. Electric Power Automation Equipment, 2010, 30(8): 81-83.
[16] 高俊莹, 徐建军, 许爱华, 等. 风能利用系数模糊控制策略的研究[J]. 电气技术, 2009(8): 36-42.Gao Junying, Xu Jianjun, Xu Aihua, et al. Study on fuzzy control strategy of wind energy utilization factor[J]. Electrical Engineering, 2009(8): 36-42.
[17] 吴正泳. 低风速条件风力发电机组的初步研究[D].北京: 华北电力大学, 2008.
[18] 刘雪菁. 变速恒频风力发电系统的运行控制及仿真分析[D]. 太原: 太原理工大学, 2006.
[19] 薛娟妮. 直驱风电系统最大功率捕获技术的仿真研究[D]. 南宁: 广西大学, 2006.
[20] 许洪华, 倪受元. 独立运行风电机组最佳叶尖速比控制[J]. 太阳能学报, 1998, 19(1): 30-35.Xu Honghua, Ni Shouyuan. FD7-5kW wind turbine generator and its control utilizing claw-pole brushless self-excited generator[J]. Acta Energiae Solaris Sinica,1998, 19(1): 30-35.

