车载全景相机的影像匹配和光束法平差

季顺平，史 云

1.武汉大学 遥感信息工程学院，湖北 武汉430079；2.东京大学 空间信息研究中心，日本 东京

1 引 言

传统胶片和CCD面阵相机由于平面成像的方式、视场狭窄，易受遮挡影响，有时无法满足特定的应用需求。而具有大视场的成像设备，如鱼眼镜头和全景镜头等，则能够克服视场狭窄的问题；特别是全景视觉成像具有成像一体化、360°大视场、旋转不变性等优点，已经在机器人、计算机视觉等相关领域中逐步得到应用，如用于视频监控、交通监督、虚拟现实、机器人导航、场景重建等，和传统成像系统相比具有明显的优越性。全景视觉亦成为计算机视觉领域一个重要的研究分支［1－2］。

基于车载传感器的高精度城市三维场景重建一直是热点问题。传统的方法是在车体上安装立体相机或更多的平面相机，然后对单相机影像进行精确匹配［3］、平差、定位、拼接，最后再建立场景模型［4］。显然，这种方法所建立场景模型的精度依赖于前期的单相机的定位以及拼接的结果。由于平面单相机间具有较大的旋角，导致配准困难，特别是拐弯时易造成部分场景成像缺失，使得影像间的精确拼接成为难点之一。相反的，全景相机一个投影中心，360°全景成像的特性，不存在场景缺失和场景拼接问题，其优势是显而易见的。目前，全景相机和全景视觉的研究在测绘领域仍处于起步阶段，主要集中在全景相机几何标定、辐射分辨率改善等前期步骤，多数情况下仅被用于全景成像［5］，应用相对较少。文献［1］针对全景相机投影过程的非线性特点，以相机运动估计和场景重建为应用背景，提出了新的标定方法。文献［2］ 建立了单反射面全景成像的几何模型并分析了不同反射面的特性，提出了全景超分辨率图像复原算法。文献［6］提出了一种使用极线几何与三角几何相结合的方法，实现基于全景图像的视觉伺服运用于移动机器人的研究。文献［5］研究了旋转式全景相机的传感器成像模型和自检校方法，并对定位精度作了详细的分析。这些方法和试验主要根据室内检校场进行，为全景相机的检校、标定打下了良好的基础。

从以上文献可以看出，全景相机的研究工作仍集中于辐射改善与几何标定等前期步骤，在实际应用中的研究和分析较少，如车载全景相机的影像处理方法、精确定位理论、场景建模技术等。其中，全景相机的精确定位是后期场景重建等工作的前提。本文着重研究了基于车载全景相机的影像自动匹配和光束法区域网平差，并对全景相机所能达到的定位精度作了较详细的分析。

2 鱼眼相机影像多特征匹配

本文采用的全景相机系统Ladybug［7］由6个独立的相机组成。5个相机按照72°水平角环形布设于车四周，第6个相机指向天空。车行驶方向的相机为0号相机，其他依次为1～4号相机。所有的相机在几何上共享一个投影中心，形成全景相机。每个独立的相机为鱼眼相机，以合成高精度的全景影像。单鱼眼影像及对应的全景影像如图1。

图1 全景影像和独立鱼眼影像Fig.1 Panoramic and mono－scene images

相对于平面成像而言，鱼眼相机的形变较大，而全景影像形变更大，本文首先在单景鱼眼影像中初匹配，再投影到统一的全景坐标进行粗剔除和二次精匹配。匹配的常用算法包括基于局部窗口的亮度相关及最小二乘匹配［9，10］，这种局部窗口灰度相关技术需要较好的匹配初值；或者具有初始几何参数，可用于立体像对间的初步纠正，然后再进行相关［11，12］。

近景影像由于拍摄角度的任意性，不再具有恒定的重叠度和旋转角。不仅需要考虑窗口灰度间的平移和灰度线性变化，还需要处理窗口间的旋转、缩放、仿射等形变；在几何关系未知的前提下，使用更为高级的特征匹配方法，如SIFT［13－15］、SURF［16］等。

针对鱼眼影像自身的特性，本文选择采用多特征的匹配算法进行，以获得可靠匹配点。

2.1 多特征初匹配

首先采用抗缩放抗旋转的SIFT算子进行匹配，获得了一定数量的匹配点。然后，引入GPS／IMU数据进行多光线前方交会，借助前方交会的误差椭圆初步剔除误匹配点。若GPS／IMU数据精度较低，则利用相对定向和模型连接进行几何约束，同时进行粗差剔除。粗差剔除后可保证不存在明显的粗差点对。

SIFT算子虽然可以克服旋转和缩放，并能够获得一些可靠的同名点，但SIFT所提取的道路特征很少（图4中的十字为SIFT特征）。对于SIFT的特征提取方式而言，直角特征过于简单，且道路背景色彩单一，因此这些斑马线角点不属于SIFT特征。由于无法识别大部分道路特征，SIFT所获得的匹配点一般位于较远的建筑上。由之而来的问题是：通过测量中交会角与交会精度的关系可知，交会角越小，交会精度越低。特别是0号相机正前方的远距离区域，交会角接近于0，因此，某些超远距离的匹配点对后面的平差步骤几乎毫无用处，甚至可能降低平差精度。

本文采用Forstner角点提取算子，以获得更多近距离的道路特征点。Forstner特征提取后，进行灰度相关以获得正确的匹配点。通过以上对车载影像的分析可知，立体像对间存在较大的比例尺变化，传统的灰度相关无法处理。本文采取两种改进策略以保证匹配的正确性。首先，根据路面条件约束搜索窗口。采用LiDAR扫描数据获得道路高度，再联合GPS／IMU数据来确定搜索区域，即主要搜索道路上的特征。若Forstner特征明显高于地面，则在搜索区域内无法搜索到同名点。其次，选择较小的匹配窗口，以保证只匹配角点区域。虽然相邻两幅影像中斑马线缩放在2倍以上，但是在角点匹配窗口内，不受缩放的影响。通过对搜索窗口和匹配窗口的调节，可获得较多高质量的道路特征点（图4中的圆为Forstner角点）。

2.2 物方约束的精匹配

SIFT和Forstner特征匹配精度在像素级，可在初步平差后进行最小二乘匹配，以提高连接点精度；并且，精匹配步骤考虑道路拐弯或交叉时车辆的行驶方向改变而造成同一场景出现在相邻鱼眼相机上的情形（如0号相机的场景位于1号相机中）。借助相机的全景成像，旋转不变性的优势，以给定最小二乘参数初值。如图2所示，在两个不同角度的摄站点S1、S2对同一物体O曝光，全景影像间的只存在一个水平角度k的形变，其夹角等于两摄站与物体间的夹角，该角度可通过已知的物点坐标和外方位元素根据三角公式计算。因此最小二乘平差的初值可根据下式设置

式中，λ为缩放系数，即两摄站到物点的距离之比。计算得到最小二乘仿射系数

图2 全景影像的水平角形变Fig.2 Horizontal angle changes between stereo panoramic images

在解求最小二乘参数的同时，利用基于多片前方交会的物方约束的几何方程求解物点的坐标增量（ΔX，ΔY，ΔZ），实现全景影像物方约束的二次匹配。式（3）为对应的线性化公式，vg为灰度方程改正数，ci为系数项，vG为几何方程改正数，几何方程如式（7）所示

3 全景相机光束法平差

3.1 全景相机成像几何模型

本文中连接点在鱼眼图像坐标系获得，而区域网平差则是在全景球面坐标系中进行，首先需要将鱼眼坐标转换为全景坐标。

在几何上，从6个不同球心、不同半径的独立鱼眼相机所在的球面直接到的全景坐标系的转换非常复杂。因此，连接点需要经过两步转换，即从单独鱼眼图像坐标系到理想平面坐标系、再到统一的全景坐标系。如式（4）所示，Kr为从第r个鱼眼相机拍摄的图像坐标X到理想平面坐标的转换矩阵，包括径向、切向畸变多项式、像主点偏移量；Rr为第r个鱼眼相机理想平面到全景相机坐标系的旋转矩阵；Tr为第r个鱼眼相机中心到全景相机中心的偏移矢量，以上3组参数都经过严密的内业检校，为固定值。λ为从平面坐标到全景球面的比例系数，每个像点各不相同

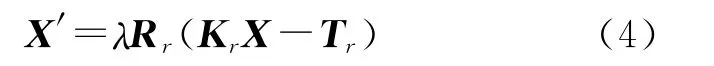
如图3所示，相邻的独立鱼眼相机间有微小的重叠，投影中心分别为Tc、T′c，uc、u′c为一对同名像点，根据式（4）转换到以G为中心的全景坐标时，需保证其全景坐标相同，即Sc、S′c重合。显然，过x点的球面将是最佳的选择。当全景球面不过x点或者对于其他同名点，则可能产生投影误差。然而，由于各独立相机的投影中心与G距离很近，该投影误差是微小值，在一定的距离内仍远小于1像素。全景球面半径的最佳距离可通过式（5）进行计算。式（5）中，ΔSg表示鱼眼相机投影中心到G的距离，N为水平相机个数。Ladybug全景成像系统中N为5，ΔSg事先已经过严密的室内检校获得，代入计算得到最佳成像距离位于距全景相机中心24m处。获得投影球面后，根据全景坐标⊗′位于球面上的约束条件，将式（4）代入球面方程可计算出每个像点的比例系数λ，同时也计算了⊗′。

获得全景相机坐标X′后，建立全景相机与大地坐标之间的几何关系。全景成像与传统胶片／数码相机成像方式区别在于，传统像片成像于一个理想平面上，所有的z坐标绝对值都等于焦距f。而全景像片的坐标X′位于球面上，z坐标都互不相同。但三点共线的几何关系依然成立，即像点与对应物方点的坐标仍然满足透视变换，如式（6）所示。式中R、T分别为地面点XA与X′的旋转矩阵与平移矢量。代数形式如式（7）所示

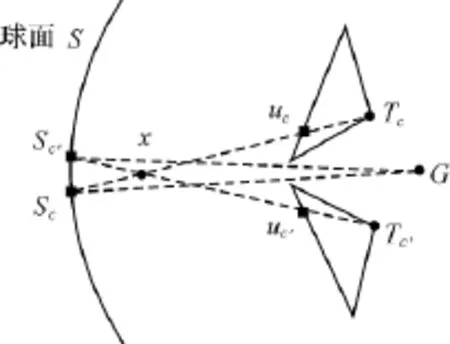
图3 独立相机理想平面坐标到全景相机的转换示意图Fig.3 Coordinate transform from rectified monocamera to panoramic camera

3.2 全景相机GPS／IMU辅助光束法平差

式（4）和式（7）构成了全景相机的共线条件方程。全景坐标系下每个像点具有独立的z坐标，并且所有像点位于同一球面上。以方程（7）为基础，构建GPS／IMU约束的无地面控制光束法区域网平差方程

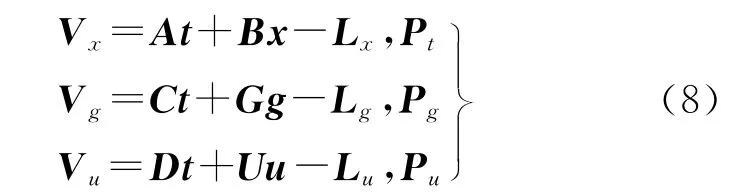
式中，Vx为像点坐标观测值的改正数；t＝［ΔXSΔYSΔZSΔφΔωΔκ］、x＝［ΔXΔYΔZ］分别为外方位元素增量和加密点地面坐标增量；A、B为相应的系数矩阵，由公式（4）线性化获得；Lx为常数项。

第2个方程为GPS观测方程，C为设计矩阵，从下式线性化获得

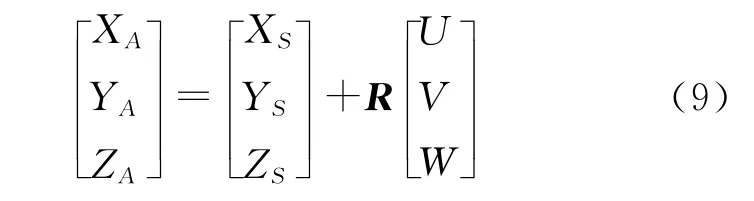
式中，XA、YA、ZA为GPS观测值；R为旋转矩阵；U、V、W为固定值，是通过精检校获得的投影中心与GPS中心的3个距离分量；Pg为相对于像点坐标观测值的权。第3个方程为IMU观测方程。设计矩阵D，从下式线性化获得

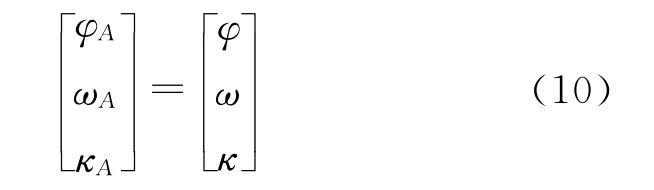
式中，φA、ωA、κA为IMU 观测值；φ、ω、κ为待求外方位元素角元素；Pu为相对于像点坐标观测值的权。

根据误差方程（8）构建法方程（11），并进行求解

式为稀疏带状矩阵，消去加密点未知数x，可获得带宽为像片最大重叠度的、只含有像片外方位元素的改化法阵［18］。然后求解出像片未知数t，再回代求解出x。通过选权迭代法［19］，逐步修正像点坐标观测值的权，或采用RANSAC方法［20］，剔除错误的匹配点对，直到结果收敛。

3.3 全景坐标观测权的设定

在式（8）中，Pt为像点观测值初始权，平差中一般初值设为单位阵。在本文的全景相机平差中，顾及两方面因素，需为其设定初值。一方面，摄站间基线很短而特征点景深变化非常大。例如，前视鱼眼相机所拍摄的车辆正前方的特征点间的交会角非常小，交会精度很差，当这类点个数很多时，将可能影响平差结果。另一方面，从图3可以看出，各独立相机投影到理想的球面形成全景坐标，距离该理想球面越远，相机间的拼接误差越大，在到达一定距离之后，拼接误差将大于1像素。由于这两方面的影响都与距离有关，本文根据物体到全景投影中心的距离设定观测值的初始权

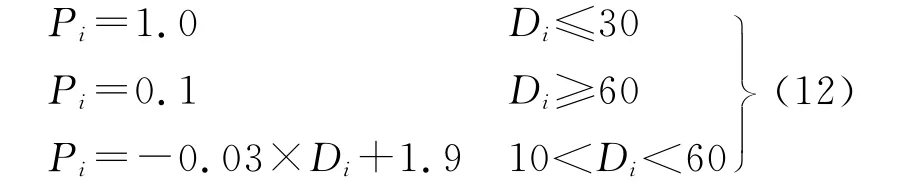
式中，Pi为第i点的初始权值；Di为第i点的物距，权值在平差过程中由选权迭代法自动更新。

4 试验结果和分析

4.1 试验设计

为验证本文方法的正确性、LadyBug全景成像系统的定位精度以及GPS、IMU数据的稳定性，选用500张全景影像序列进行了自动匹配和GPS／IMU约束的无地面控制平差试验，共包含3000张独立鱼眼影像，总拍摄长度约1km。由于天空上没有特征点，匹配时未匹配天空的影像，故匹配一共在2500张影像上进行，而平差则是在全景坐标系中进行。所采用的GPS／IMU系统的定位精度约5～20像素。

LadyBug拍摄鱼眼影像大小为1616像素×1232像素，像元分辨率为0.009mm，颜色分辨率为8bit量化的RGB色彩空间、采用每秒15帧压缩JPG格式。独立鱼眼相机的焦距为3.3mm，投影中心相互距离约40mm，全景影像球面成像于距离球心24m处。

4.2 试验结果和分析

4.2.1 影像匹配试验和分析

图4为鱼眼相机匹配结果。

连接点提取在0～4号水平相机影像上进行，为加快匹配速度，只匹配影像中间的感兴趣区域，影像上方的天空和影像下方的测量车所处区域已经被滤除，如图4所示。其中，十字表示SIFT匹配点，圆圈表示Forstner匹配点。Forstner特征仅考虑道路上明显的角点。根据GPS／IMU及LiDAR精度，确定搜索区间为31像素×31像素。根据斑马线角点的大小，匹配窗口选择为11像素×11像素。

分析匹配结果可以发现：

（1）图4中1、2、3号的立体像对的场景中含有较为丰富的地物特征，包括路旁的建筑物和大量道路上的交通标志线。无论是SIFT特征或者Forstner特征都匹配出了很多同名点。但SIFT特征点大都出现在结构比较复杂的建筑物和一些树木上，近距离的道路匹配点很少；而Forstner特征匹配弥补了这部分区域的匹配点，充分保证近距离可靠的连接点对平差的贡献度。

（2）在图4（d）中，由于没有建筑物，匹配点集中于主干道和人行道的边界上。而在4（e）中，一共只有5对同名点获得正确匹配，这由缺少人工地物以及影像间存在巨大的变形引起。因此，如果采用传统的平面相机成像、独立平差后再拼接的方法，则无法处理图4（e）这种缺乏连接点的影像，从而导致定位失败和场景缺失；4（d）由于连接点分布不均也可能导致平差无法正确收敛。而全景相机优势体现在将所有单相机拼接成整幅全景影像之后，再进行平差，因此，借助于0、1、2号影像中的大量连接点，部分单独相机的匹配失败不会对平差结果造成影响。

图4 鱼眼相机匹配结果Fig.4 Matching results of mono－scene images

4.2.2 光束法平差试验和分析

在验证本文匹配和平差方法在全景影像序列处理中的可行性的同时，还与和以下两种传统的处理方法进行对比。第一，只采用计算机视觉中经典的SIFT特征提取连接点，然后用SIFT连接点进行平差。第二，采用本文的方法进行匹配，但权阵初值设定为单位阵。3种方法的平差结果一并列于表1。在物方残差一栏中，只有小于60m的连接点被统计。

表1 平差结果Tab.1 Adjustment result comparison of three methods

从LadyBug全景成像的几何理论而言，距离理想全景球面越远，成像效果越差、定位精度越低。为评价该全景成像系统在不同距离上的定位精度，对连接点物方坐标残差作了统计，如表2所示。

表2 不同距离连接点的物方残差Tab.2 RMS differences of object coordinates in different range m

为评价LadyBug全景成像系统所采用的GPS／IMU组合导航系统的内部稳定性，统计了原始外方位元素与平差后的外方位元素的残差，如表3所示。

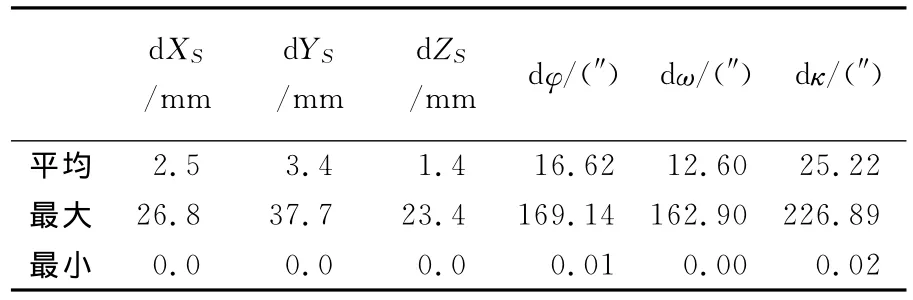
表3 GPS／IMU外方位元素残差Tab.3 Differences between GPS／IMU and EOs after adjustment

分析以上结果可以发现：

（1）从表1可以看出，3种方法对外方位元素未知数的解算精度都是非常高的，反映方程解算的正确性和区域网内部的精度一致性；本文方法（加权）和本文方法（未加权）的精度基本一致，SIFT匹配方法平差获得的外方位精度相对较低。

当仅采用SIFT进行连接点的自动提取时，其观测值的平差中误差最大，接近1像素，这和SIFT自身的定位精度是相当的；由于大部分的连接点位于距离较远的建筑物上，交会精度和全景拼接精度较低，导致很多可能正确的匹配特征被剔除，每张影像只有平均19个连接点。并且，物点的交会残差在3种方法中也是最大的。

采用本文的多特征匹配策略，观测值中误差明显提高，达到0.29像素。同样的，加密点物方交会的精度也获得了明显的提高，3个方向的残差都在4cm以下，z方向的残差甚至达到了5mm。然而，由于没有设置正确的初始权值，导致大量的连接点被剔除，最终每张像片只有27个连接点被保留。

采用本文的多特征匹配策略和加权方法，观测值中误差得到进一步的提高，达到0.22像素，并且交会精度在3个方向上都高于4cm。虽然和未加权方法的精度相当，但由于按照距离设置了初始权，使得连接点的个数得到了明显的提升，达到75个。因此，对加密点距离的远近进行加权，和实际情况相符，所以加权后能够保证大量的连接点被正确保留。

（2）表2进一步证实了受交会角、全景相机拼接技术的综合影响，成像距离对全景相机平差精度影响明显。随着距离较远的物方点加入统计，3个方向的交会精度都逐渐降低，且其拐点出现在60m左右。当地面点到摄站的距离小于60m时，空间交会精度可达到4.5cm，而当距离增加到80m，交会精度则降到了17.4cm。因此，LadyBug全景成像系统的最佳定位范围在50～60m之内，超过该距离不适宜将全景几何模型应用在精确定位中。

事实上，根据全景相机的成像原理也可从理论上进一步验证该结论。将系统参数代入式（5）可知，全景投影球面位于24m处，此时求的交会角约0.048°，距离60m时，投影误差约3cm。距离100m时，投影误差为8.3cm。物体距离该投影球越远，同名点间投影误差越大。随着同名点精度的下降，该投影误差在平差过程中实际上被进一步放大。

（3）从表3可以看出，线元素的平均残差高于4mm；φ、ω角元素的平均残差分别为16″和12″；κ角精度稍低，为25″；总体而言，稳定性非常好。但是也存在个别误差较大的外方位元素，线元素最大残差接近4cm，是平均残差的10倍左右；角元素最大残差也达到了平均残差的10倍。虽然本文将GPS／IMU约束的区域网平差结果作为真值与GPS／IMU原始值进行比较，但平差结果与实际真值之间差异很小，说明LadyBug系统所采用的GPS／IMU系统的内部稳定性是非常高的。

5 结 论

由于成像机理的差异，全景相机影像的匹配和平差过程都和传统近景平面相机有一定的区别。本文通过多特征匹配的方法，利用Forstner特征、SIFT特征进行联合匹配和全景几何约束的二次精匹配，获得了高稳定度的连接点。然后推导了全景相机的几何成像模型，并联合GPS／IMU数据进行了光束法区域网平差。通过试验，验证了本文方法具有匹配可靠性好、平差结果稳定且交会精度高于5cm。此外，还获得了Lady－Bug全景成像所获取场景在60m内可获得最佳的定位精度的结论。若需要获取更高精度的定位结果，应当采取在独立鱼眼相机进行平差的方法，而不适宜在全景坐标下进行。

本文的GPS／IMU辅助区域网平差能够较好地说明网形的内部精度，但GPS／IMU的实际精度评价、场景定位精度检查以及系统误差改正只能通过引入控制点平差完成，这是后续要开展的工作。

［1］ ZHANG Lei.Central Catadioptric Imaging System Modeling［D］.Hangzhou：Zhejiang University，2010.（张雷.单视点折反射成像系统的建模、标定与应用［D］.杭州：浙江大学，2010.）

［2］ XIAO Xiao.High Resolution Panoramic Imaging System and Visual Application［D］.Hangzhou：Zhejiang University，2009.（肖潇.高分辨率全景成像系统及其视觉应用研究［D］.杭州：浙江大学，2009.）

［3］ ZHANG Ka，SHENG Yehua，YE Chun.Digital Close－range Stereo Image Matching Based on Digital Parallax Model and Improved SIFT Feature ［J］.Acta Geodaetica et Cartographica Sinica，2010，39（6）：624－630.（张卡，盛业华，叶春.基于数字视差模型和改进SIFT特征的数字近景立体影像匹配［J］.测绘学报，2010，39（6）：624－630.）

［4］ TU Zhenbiao，LIU Yongcai，SU Kang，et al.A Modeling Method for Large Scale Terrain Oriented 3DDisplay［J］.Acta Geodaetica et Cartographica Sinica，2004，33（1）：71－76.（涂震飚，刘永才，苏康，等.一种面向大场景3维显示的地形建模方法［J］.测绘学报，2004，33（1）：71－76.）

［5］ PARIAN L A，GRUEN A.Sensor Modeling，Self－calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners ［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2010，65（1）：60－76.

［6］ YANG Shaoping，CHEN Xiong，KONG Qingsheng.Imagebased Visual Serving for Mobile Robots with Central Panoramic Camera ［J］.Computers Engineering and Design，2010，31（19）：4261－4264.（杨少平，陈 雄，孔庆生.采用全景相机的移动机器人视觉伺服［J］.计算机工程与设计.2010，31（19）：4261－4264.）

［7］ IKEDA S，SATO T，YOKOYA N.High－resolution Panoramic Movie Generation from Video Streams Acquired by an Omnidirectional Multi－camera System ［C］∥Proceedings of the Multisensor Fusion and Integration for Intelligent Systems.［S.l.］：IEEE，2003.

［8］ SATO T，IKEDA S，YOKOYA N.Extrinsic Camera Parameter Recovery from Multiple Image Sequences Captured by an Omni－directional Multi－camera System ［C］∥Proceedings of the 8th European Conference on Computer Vision.［S.l.］：Springer，2004.

［9］ ACKERMANN F.High Precision Image Correlation［C］∥In the Proceedings of the 39th Photogrammetric Week.Stuttgart：［s.n.］，1984.

［10］ ZHANG Li，GRUEN A.Multi－image Matching for DSM Generation from IKONOS Imagery［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2006（60）：195－211.

［11］ JI Shunping，YUAN Xiuxiao.Automatic Matching of High Resolution Satellite Images Based on RFM ［J］.Acta Geodaetica et Cartographica Sinica，2010，39（6）：592－598.（季顺平，袁修孝.基于RFM的高分辨率卫星遥感影像自动匹配研究［J］.测绘学报，2010，39（6）：592－598.）

［12］ KORNUS W，ALAM U′S R，RUIZ A，et al.DEM Generation from SPOT－5 3－fold along Track Stereoscopic Imagery Using Autocalibration［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2006，60（3）：147－159.

［13］ LOWE D G.Object Recognition from Local Scale－invariant Features［C］∥Proceedings of the 7th IEEE International Conference on Computer Vision.Kerkyra：［s.n.］，1999.

［14］ LOWE D G.Distinctive Image Features from Scale－Invariant Keypoints［J］.International Journal of Computer Vision，2004，60（2）：91－110.

［15］ SINHA S N，FRAHM J M，POLLEFEYS M，et al.GPU－based Video Feature Tracking and Matching［R］［S.l.］：UNC Chapel Hill，2006.

［16］ BAY H，ESS A，TUYTELAARS T，et al.Speed－Up Robust Features（SURF）［J］.Computer Vision and Image Understanding，2008（110）：346－359.

［17］ KANNALA B.IEEE Transactions on Pattern Analysis and Machine Intelligence ［J］.TPAMI，2006（28）：1335－1340.

［18］ LI Deren，ZHENG Zhaobao.Analytical Photogrammetry［M］.Beijing：Suveying and Mapping Press，1992.（李德仁，郑肇葆.解析摄影测量学［M］.北京：测绘出版社，1992.）

［19］ LI Deren，YUAN Xiuxiao.Error Processing and Reliability Theory［M］.Wuhan：Wuhan University Press，2002.（李德仁，袁修孝.误差处理与可靠性理论［M］.武汉：武汉大学出版社，2002.）

［20］ FISCHLER M A，BOLLES R C.Random Sample Consensus：A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography［J］.CACM，1981，24（6）：381－395.