斜抛运动中射程问题的一般性讨论与数值计算

琚 鑫

(北京市第十五中学 北京 100054)

岳凌月

(首都师范大学物理系 北京 100048)

王邦平

(首都师范大学附属中学 北京 100048)

1 问题的提出

抛体运动是物理学中最基本、最重要的一种二维曲线运动之一.在地球表面附近不太大的范围内，重力加速度g可以看成常量.如果在整个抛体运动过程中，速度也不很大的情况下，可以忽略空气阻力，则抛体运动的水平分量与竖直分量相互独立，使问题大大简化.描述抛体运动的物理量主要有速度(分速度、合速度)、位移(分位移、合位移)和轨迹方程.

抛体运动的射程问题是个有趣的课题.对于初速度与末速度在同一水平面上的抛体运动而言，如文献[1]所述，抛体所能达到的最远点称为射程(本文亦采用此定义)，记为xm，计算可得

但是，如果初速度与末速度不在同一水平面上，而是有一段高度差h，那么，此时的射程是多少？最大射程与初速度v0，出射角θ，高度差h之间的关系如何？这就是本文要讨论的问题.

2 模型与理论推导

如图1所示，在距离地面h处抛出一个物体(可看作质点)，其初速度为v0，与x轴夹角为θ.忽略空气阻力，则抛体运动的水平分量与竖直分量相互独立.在竖直方向上，物体做竖直上抛运动.在水平方向上，物体做匀速直线运动，由此可以得出物体的两个分位移与时间t的关系，即运动方程为

图1

消去时间参数t，即可得到轨迹方程

抛物线与x轴正半轴的交点坐标即为射程L，解方程为

由此，射程L的表达式为

(1)

3 数值计算与讨论

我们研究射程L与初速度v0和高度差h的关系，观察v0与h对L-θ曲线[2]的影响.

图2

图2显示了在高度差h恒定的情况下，不同的初速度对射程L的影响.绘图时，参数选取为

h=2mg=10m/s2

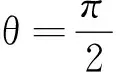
(1)初速度决定射程的大小.在出射角度θ一定的情况下，随着初速度的增加(从5 m/s到8 m/s)，物体的射程L越来越大，且不同初速度下的L-θ曲线彼此不相交，也就是说，在出射点与落地点存在高度差的情况下，我们不能使出射角度相同、出射速度不同的两个斜抛运动达到同样的射程.

(2)射程存在最大值θC.在出射角θ小于某一个角度值θC时，射程随着出射角θ的增加而增加，当出射角θ大于θC时，射程随着出射角θ的增加而减小.

(3)最大射程依赖于θC.从图2中可以看出，随着v0的增加，射程取得最大值时对应的角度θC会向θ增大的方向移动.这与h=0时，最大射程与出射角无关的结论不同.

(4)当θ<θC时，射程随θ的增加呈现较慢的增加，当θ>θC射程随θ的增加呈现较快的衰减.

(5)当初速度v0较小时，θ在相当宽的一个区间内,对应的射程与最大射程相差不多.当初速度v0较大时，射程对θ的取值变得越来越敏感.

图3

图4

另一个有趣的问题是，当初速度和高度差的值给定后，能不能求出最大射程所对应的出射角θC.答案是肯定的.我们只需将式(1)对θ求导数既可得

令其等于零，就可求出相应的出射角θC，即解方程

(2)

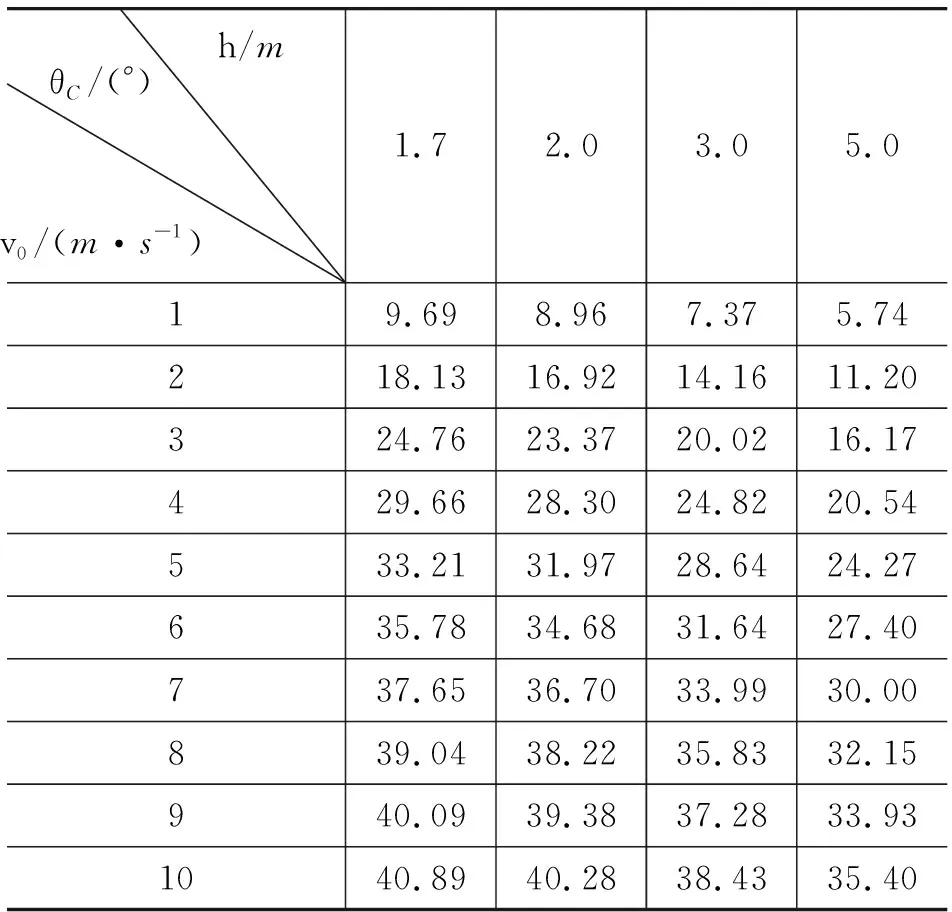
表1 式(2)的数值解

从表中分析可知，在射程取得最大射程Lmax时，出射角θC与初速度v0近似满足对数关系，即

θC=alnv0+b

其中a和b是待定系数，可由实验测定.我们对此亦作了数值计算，其中a近似稳定在14.1左右，b随h的变化较为明显，近似满足b∝h-1.

注：高度差h不可太大，否则质点的运动速度将较大，从而空气阻力就不可忽略不计了.

参考文献

1 赵凯华,罗蔚茵.新概念物理教程·力学(第二版).北京：高等教育出版社，2004

2 Mathematica Demystified, Jim Hoste, McGraw-Hill, 2009