宇航员失重问题讨论

张艺芳 李惠玲

(山西师范大学物理与信息工程学院 山西 临汾 041004)

宇宙飞船绕地球飞行的过程中，宇航员会处于失重状态.失重不仅给宇航员造成工作、生活的诸多不适应，还会对他们的身体产生极大影响.那么，失重的主要原因是什么？失重的程度如何呢?

本文以“神州七号”载人飞船为例，从力学角度讨论宇宙飞船绕地球飞行过程中宇航员的失重问题.

1 宇宙飞船在近地点和远地点的飞行速度

由牛顿力学知，宇航员在非惯性系中不仅受作用力，而且受惯性力，要知道宇航员所受惯性力的大小和方向，就必须先求出宇宙飞船的飞行速度.

太空中有许多星体，它们对宇宙飞船都施有万有引力.由于太阳系之外的群星到宇宙飞船的距离远远大于地球到飞船的距离,故它们对飞船的万有引力微不足道,太阳系诸行星的质量远远小于太阳的质量，与太阳相比它们对飞船的万有引力当然可以忽略. 因此,在分析飞船的受力时,就无需考虑太阳系之外的群星及太阳系诸行星的影响了.

下面我们先来计算宇宙飞船所受太阳、地球和月亮的万有引力.

设宇宙飞船所受太阳、地球和月亮的万有引力分别为Fs,Fe,Fm，飞船飞行的近地点高度

hn=200 km

远地点高度

hf=350 km

宇宙飞船的质量

M=8×103kg

地球的质量

Me=5.976×1024kg

太阳的质量

Ms=1.99×1030kg

月球的质量

Mm=7.35×1022kg

万有引力常量

G=6.67×10-11N·m2/kg2

地球半径

Re=6.37×106m

日地距离

rs=1.496×1011m

月地距离

rm=3.84×108m

图1

当太阳、地球、月亮及飞船位于图1所示的位置时，由万有引力定律

可得太阳对飞船万有引力的表达式

代入数据得

Fs=4.745×10 N

地球对飞船的引力

代入数据得

Fe=7.061×104N

月亮对飞船的引力

代入数据得

Fm=2.755×10-1N

由上述计算结果可看出，宇宙飞船所受太阳和月亮的最大万有引力比地球对它的最小万有引力小3个数量级以上，所以,在我们所讨论的问题中Fs和Fm是可以被忽略的.

选地球为近似的惯性系，宇宙飞船在地球的万有引力作用下绕地球做椭圆运动，飞船在近地点和远地点的速度v1和v2如图2所示.

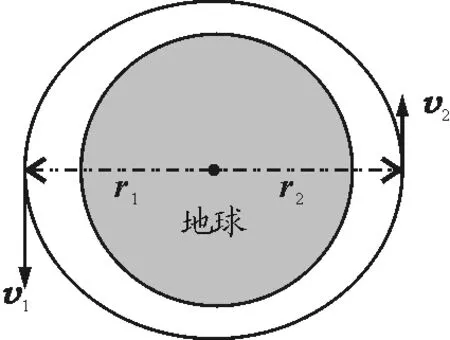
图2

由角动量守恒定律得

r1Mv1=r2Mv2

由机械能守恒定律得

两式联立得

v1=7.833×103m/sv2=7.658×103m/s

2 宇航员的失重情况

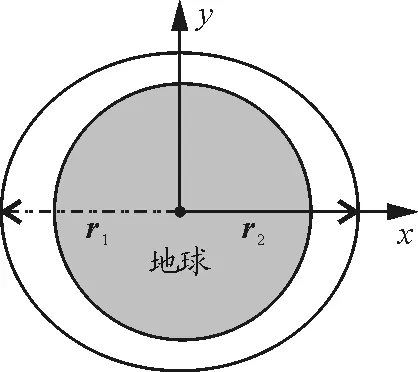
图3

坐标系如图3所示，设宇航员质量m=70 kg,宇宙飞船在近地点时，地球对宇船员的引力

代入数据得

fe=6.464×102

飞船对宇航员的引力

将飞船近似抽象成一半径为R的均匀球体，宇航员抽象成质点，r表示宇航员到飞船质心的距离，因为r→0，所以f→0.

(取ρ≈Re)，宇航员在近地点的“重量”

宇航员失去的重量为

ΔG近=mg-G近

代入数据得

ΔG=(70×9.8-27.8) N=658.2 N

同理，在远地点时

宇航员在远地点的“重量”

宇航员失去的重量为

ΔG远=mg-G远

代入数据得

ΔG远=659.4 N

在轨道的其他点宇航员的失重值与远、近地点差别不大，在此就不详细计算了.

由上述计算可知，宇航员在飞船中不仅把95%以上的重量失掉了，而且宇航员所受“重力”的方向还是背离地球的，即当宇航员站立时，他的头是朝向地面的.

参考文献

1 赵凯华，罗蔚茵.新概念物理教程·力学(第一版).北京:高等教育出版社，1995

2 漆安慎，杜婵英.普通物理学教程·力学(第二版).北京:高等教育出版社，2005

3 神舟七号载人飞船.http://baike.baidu.com/view/1401886.htm