一种特殊的单位制——“准自然单位制”

蔡志东

(镇江高等专科学校丹阳校区教师教育系 江苏 丹阳 212300)

1 引言

迄今为止，众多文献[1～4]在介绍自然单位制时，都没有对自然单位制的来龙去脉和本质特征进行详细的阐述.比如为什么要引进自然单位制？为什么能够引进自然单位制？为什么可以随意地令常数c=ћ=G=me=e=1？能否随意地令阿伏伽德罗常数NA=1？

本文将围绕这些问题，对自然单位制的来龙去脉和本质特征进行详细的阐述，并纠正一些人的错误认识.通过引入“准自然单位制”的概念，帮助读者更好地理解自然单位制.

2 国际单位制简介

2.1 国际单位制中的基本单位和辅助单位

国际单位制是目前应用最为广泛，也是大家最熟悉的单位制.其基本单位有7个，即时间单位秒(s)、长度单位米(m)、质量单位千克(kg)、电流单位安培(A)、热力学温度单位开尔文(K)、发光强度单位坎德拉(cd)、物质的量的单位摩尔(mol),此外还有两个辅助单位即平面角的单位弧度(rad)、立体角的单位球面度(sr).

2.2 国际单位制中的基本单位与基本物理常量之间的关系

国际单位制中的7个基本单位和基本常量有一定的关系，见表1.

表1 与基本单位相关的基本常量

注：表1仅仅列出了一部分与基本单位相关的基本常量，而没有列出所有的相关常量.此外，力学中的三个基本单位s，m，kg也并不是和三个常量ћ,c,G一一对应(正因为如此，这三个表格中的线为虚线而非实线).常数π与发光强度相关是因为整个空间的立体角为4π.

3 国际单位制的缺陷

自国际单位制推广以来，各国科学家采用统一的单位描述自然现象和规律，这对科学进步和普及起到了巨大的促进作用.但是这个单位制也有一些不足，如基本单位定义的随意性.究竟多长的时间叫做1 s？多长的距离叫做1 m？多少物质叫做1 kg？——这都是人为的约定(当然不是绝对的随意，它的定义至少必须方便日常生活以及尽可能便于精密测量). 由于这种随意性，导致了基本单位量度上的不精确性，应用上的局限性，逻辑上的不统一性.因此，寻找一种自然的，精确的单位制就是一种必然.

4 几种常见的自然单位制

表2列出了几种常见的自然单位制.自然单位制和SI制不同，它的基本单位不是随意规定的，而是根据基本物理常量得出的，并且7个量纲缩减为一个量纲.

表2 常见自然单位制一览表

5 “准自然单位制”

5.1 “准自然单位制”的概念

与众多专家学者一样，在各种自然单位制中，笔者特别推崇“普朗克单位制”，因为它的基本单位不是用某一特定粒子的特定参数来定义的，而是以普适常量来定义的.而像原子物理或量子色动力学中采用的单位制那样，以电子质量或质子质量为质量的基本单位，显得并不那么自然，其适用范围也必定相当有限.普朗克单位制是真正自然的单位制.下面我们将在此基础上引入一种和它相似的单位制——“准自然单位制” .

前面已经提到，多长的时间叫做1 s？多长的距离叫做1 m？多少物质叫做1 kg？多高温度叫做1 K？多少电荷叫做1 C？(或多大电流叫做1 A?)这纯粹是人为规定的.既然如此，我们当然可以重新定义一个新的“秒、米、千克、开尔文、库仑(安培)”，它使相关的普适常量的数值恰好等于1,即

下面来证明，我们确实可以做到这一点.

设新的“秒、米、千克、开尔文、库仑”分别用符号s′,m′,kg′,K′,C′来表示，并令新单位和旧单位之间的比例系数分别为α,β,γ,δ,λ，即

1 s′=αs,1 m′=βm

1 kg′=γkg,1 K′=δK,1 C′=λC

反之有

1 s=α-1s′,1 m=β-1m′,1 kg=γ-1kg′

1 K=δ-1K′,1 C=λ-1C′

要使“约化普朗克常量”ћ=1，也就是使

ћ≈1.055×10-34J·s=

1.055×10-34kg·m2/s=

1.055×10-34×(α/γβ2)× kg′·m′2/s′=

1 kg′·m′2/s′

即数值上有

γβ2/α=ћ

(1)

同样，要使光速c=1, 也即

c≈3×108m/s=3×108(α/β) m′/s′=1 m′/s′

于是在数值上有

β/α=c

(2)

类似地，要使万有引力常量G=1，也即

G=6.67×10-11N·m2/kg2=

6.67×10-11m3/(kg·s2)=

6.67×10-11(γα2/β3) m′3/(kg′·s′2)=

1 m′3/(kg′·s′2)

于是数值上有

β3/γα2=G

(3)

要使玻尔兹曼常量kB=1即

kB=1.38×10-23J/K=

1.38×10-23kg·m2/(s2·K)=

1.38×10-23(α2δ/γβ2) kg′·m′2/(s′2·K′)=

1 kg′·m′2/(s′2·K′)

于是有

γβ2/α2δ=kB

(4)

若要静电力常量Kj=1,即

9×109kg·m3/(s2·C2)=

9×109(α2λ2/γβ3) kg′·m′3/(s′2·C′2)=

1 kg′·m′3/(s′2·C′2)

于是有

γβ3/α2λ2=Kj

(5)

联立方程(1)、(2)、(3)即可得到比例常数α,β,γ.具体做法是把式(2)分别代入式(1)和式(3)得到

于是我们得到“新的1 m”和旧的1 m之间的关系式

将β的表达式代入式(2)可得

α,β,γ求出后就很容易求出δ,λ.

把α,β,γ的表达式分别代入式(4)和(5)可得

1.876×10-18C

上述5个比例常数α,β,γ,δ,λ数值上恰好等于普朗克时间、长度、质量、温度、电荷,即tP,lP,mP,TP,qP.由“新的库仑”和“新的秒”可以构成新的电流强度单位即新的安培A′.

1A′=1 C′/s′=(qP/tP) A=

IP即为普朗克电流.

1(cd)′/(cd)=1W′/W=1(J′/s′)/(J/s)=

1(kg′·m′2/s′3)/(kg·m2/s3)=1γβ2/α3=

即

1W′=3.628×1052W=PP=c5/G

1cd′=3.628×1052cd

这里的PP=c5/G就是普朗克功率.由此可知，我们无需重新定义新的坎德拉，由新定义的5个基本单位(即新的“秒、米、千克、开尔文、安培或库仑)完全可以确定新的坎德拉.7个基本单位中还剩下最后的一个单位摩尔没有重新定义.这最后一步最艰难，也是许多人最容易犯错误的一步！

5.2 摩尔的新定义和电子质量的关系

从原则上讲，除了纯粹的数学常数(比如圆周率π或精细结构常数α′)之外，几乎一切有量纲的物理常量均可以通过重新选择合适的单位制而使其为1，但是有一个例外，那就是阿伏伽德罗常数NA，它是绝对不可以等于1的！文献[2]为了引进所谓的自然单位制而令NA=1的做法是十分荒谬的.笔者查阅了许多文献，除文献[2]之外，从来没有哪本书中有NA=1的，文献[2]的做法是完全错误的！

摩尔这个基本单位与所有其他的基本单位有质的区别，一切其他单位，从原则上讲，其大小都可以随意变化，随意规定.比如长度单位米，你把多长的距离叫做1 m是无所谓的，随你怎么定都可以.其他如秒、千克、开尔文、库仑(或安培)、坎德拉等也是如此.但是摩尔是不能随意变化、随意规定的(当然可以在一定的范围内变化，有一定的自由度).

1971年第十四届国际计量大会规定：“摩尔是一系统的物质的量，该系统中所包含的基本单元数与0.012 kg碳-12的原子数目相等(这个数目就是阿伏伽德罗常数NA).使用摩尔时应予以指明基本单元，它可以是原子、分子、离子、电子及其他粒子，或是这些粒子的特定组合.”摩尔好似一座桥梁，把单个的、肉眼看不见的微粒跟大数量的微粒集体、可称量的物质之间联系起来.摩尔的概念最初来自于阿伏伽德罗定律.

1811年阿伏伽德罗发现了以他的名字命名的“阿伏伽德罗定律”：在标准状态下(0℃，1个标准大气压)，同体积的任何气体都含有相同数目的分子，而与气体的化学组成和物理性质无关. 反过来，由此定律可知，相同数目的任何气体分子在同体积的情况下，将产生相同的宏观压强和温度！正是基于这一点，我们才有可能和必要引入摩尔这个单位.

摩尔是物质的一种量度方法，它和质量(它也是物质的一种量度方法)不同之处在于，质量只关心物质的多少，无论量度的对象是大还是小，是单个粒子还是粒子集团(系统)都是一样的.这种量度方法的优点是统一性，其缺点是忽略了“量变质变规律”，它认为一个系统所包含的单元数不论多少都是一样的，其实不然.当一个系统所包含的粒子数较少时，系统的演化规律与单个粒子的规律相差不大(可以在单个粒子的规律基础上通过适当的数学方法求得系统的演化规律)，但是，当粒子数目多到一定程度时，量变就会引起质变，此时，系统所遵循的规律是一种统计规律，它与单个粒子的规律截然不同！一些宏观的物理量(比如压强和温度等)也只有在粒子数多到一定程度是才有意义(一个分子不存在压强，也没有宏观上的温度).

选择自然单位制的目的是为了简化规律或方程的数学形式，绝对不是推翻或否定规律.而像文献[2]那样令NA=1(即规定每一摩尔为一个粒子)，就已经完全彻底地否定了量变质变规律或统计规律.无论我们选择什么样的单位制，有一点绝对不能更改,即摩尔必须是一个沟通宏观物理量和微观物理量之间的桥梁！

由此可知，引入摩尔时，必须遵循三个基本原则：一是宏观性(一个摩尔必须是一个看得见、摸得着的宏观系统，即在质量和体积上都不能太小)；二是统计性(这个宏观系统所遵循的规律不同于少数粒子的规律)；三是温度等概念的有价值性(这个宏观系统可以用一些宏观的物理量比如温度来描述，对气态物质还可以用压强来描述).

在上述三个基本原则下，我们仍然有相当的自由度来给摩尔下一个全新的定义而不必拘泥于现在的定义.把多少粒子集团叫做一个摩尔？这是相当自由的(前提是不违反上述三个原则)，比如你把现在的1 mol(即NA=6×1023个微粒集团)的十分之一叫做一个新的摩尔(即规定6×1022个粒子集团叫做一个新摩尔)是完全可以的(这么多粒子组成的系统，其质量、体积都是看得见、摸得着的，即使是电子集团，其质量也比一粒灰尘大许多.温度也是有意义的).但是你不能把一个分子或一个电子叫做1 mol(一个粒子不是宏观系统，也没有温度与压强等概念).

当初给摩尔下定义时并没有什么绝对充足的理由(把12 g碳-12中的原子数NA叫做1 mol，一是因为12 g碳是一个宏观物质系统，二是因为碳-12的原子量可以精确测量，其实，选用别的数目也是可以的).究竟如何给摩尔下一个新的定义？笔者给出一种很奇特的方法.

新的摩尔和旧的摩尔之比

2.4×1022/6×1023=0.04=kC

这个比例常数暂时可以称之为“蔡氏常数”.即我们只需要把原先的摩尔或NA乘以4%即可得到新的摩尔和新的阿伏伽德罗常数！

至此，7个基本单位已经得到了全部改造或重新定义.新的“准自然单位制”和旧的国际单位制之间的关系如表3所示.

表3 “准自然单位制”和国际单位制基本单位之间的关系

5.3 “准自然单位制”与国际单位制之间的关系

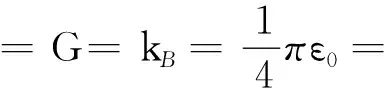
电子的电荷与普朗克电荷的比值为

这里α′为精细结构常数.即电子的电荷也可以从普适常量和精细结构常数导出.

6 “准自然单位制”和(普朗克)自然单位制的区别与联系

“准自然单位制”和(普朗克)自然单位制的区别有两点：一是前者有7个量纲而后者只有一个量纲(通常是能量的量纲)，这导致前者基本物理常量ћ,c,G,kB,K都是有量纲的，而后者大部分都是无量纲的纯数(比如光速c和约化普朗克常量ћ就是纯数字1)；二是前者给出了7个基本单位特别是发光强度坎德拉和物质的量摩尔的新定义，并由此得出了新的摩尔和电子质量的关系，而后者没有.

两者的联系是紧密的，由于一切物质归根结底是能量的不同表现形式，因此7个量纲当然可以缩减为一个量纲(如能量)，这实际上表明了自然界本质上的统一性.这样，我们不仅可以使基本物理常量的数值等于1，而且可以使它们等于一个数学上的纯数1.

笔者相信，通过本文的推导，可以使读者理解“为什么我们可以随意地令许多物理常量等于1？”，并对这些普适常量背后隐藏的秘密产生兴趣.

注：球面度为一立体角，其顶点位于球心，而它在球面上所截取的面积等于以球半径为边长的正方形的面积，在欧几里得平直时空中，整个空间的立体角为4π球面度.

参考文献

1 戴军.浅谈自然单位制.江苏广播电视大学学报, 1997,22(7):84～85

2 王文周.自然单位制.信阳师范学院学报, 1980(1):38～44

3 向安平.自然单位制.四川师范大学学报, 1990,13(1):111～112

4 曾谨言.量子力学卷1.北京:科学出版社,2000.536～537