火车汽笛声的频率变化曲线的定量分析

卞清

(解放军理工大学理学院 南京 江苏 211101)

1842年奥地利物理学家多普勒在铁路边散步时,一列火车鸣着汽笛驶过，他注意到列车驶过时,汽笛声的音调发生了变化，这引起了他的兴趣，经过研究发现，当波源和观察者相对运动时，观察者所接收到的频率和波源的频率不等，这就是多普勒效应(Doppler effect)．

电磁波也存在多普勒效应．电磁波以光速传播，电磁波的多普勒效应公式要利用狭义相对论推导．声波和电磁波的多普勒效应原理在科学研究和工程技术中都有着广泛的应用．

1 驶过静止观察者身旁的火车汽笛声频率与火车位置的关系

设波源的振动频率为ν,观察者接收的振动频率为ν′，观察者相对介质静止，波源以速度v运动．如果波源沿着与观察者的连线运动, 观察者所接收到的频率与波源的频率之比为

(1)

式中“-”是波源向着观察者运动，ν′>ν频率升高；“+”是波源远离观察者运动，ν′<ν频率下降．

当波源的运动方向与二者的连线不平行时，如图1，只要将式(1)中的波源运动速率v换为vcosθ，θ是波源运动方向与二者连线的夹角[1]

(2)

即然波源运动而观察者静止，那么波源与观察者的相对位置就是变化的，θ角就会随着波源的位置而改变．如图1中，波源S是火车的汽笛，设火车相对介质沿着x轴做匀速直线运动，汽笛t时刻的坐标

x=x(t)．观察者静止于P处(xp=0)，与火车轨道的垂直距离为d．考虑到声波传播所用的时间，观察者在t时刻接收到的汽笛发出的声波是t时刻之前的(t-Δt)时刻，汽笛位于x(t-Δt)位置所发出的.

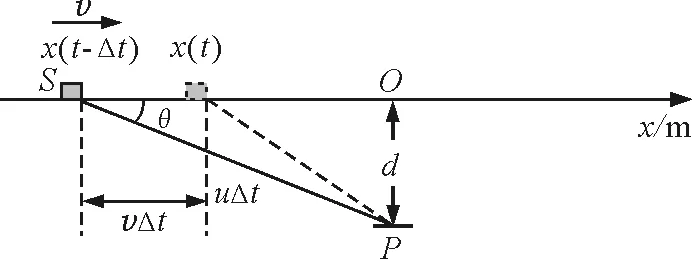
图1 波源和观察者的相对位置

注意到图中的火车坐标x(t)<0，由直角三角形SOP的边长关系可得

(uΔt)2=(x-vΔt)2+d2

(3)

夹角θ满足

(4)

式(2)、(3)、(4)联立，可解出

(5)

式(5)即为经过静止观察者旁边的火车位置与汽笛声频率的关系式,其中声波速率u=340 m/s，火车速率为v，d是观察者离火车轨道的距离．

2 计算结果与分析

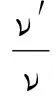
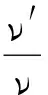
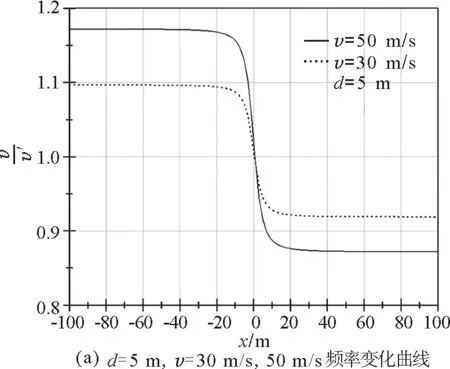
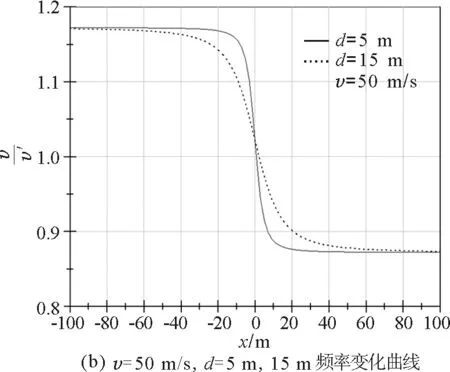
图2

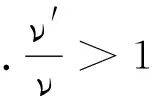
(1)图2(a)中两条曲线分别是火车速率为50 m/s和30 m/s，观察者与轨道的距离为5 m.

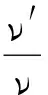
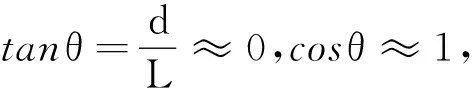
火车以30 m/s的速率运动时

在这两种速率下，频率最大相对改变量分别为

(2)图2(b)中的两条曲线分别是观察者与轨道的距离为5 m和15 m，火车速率为50 m/s

从图中可以看出,汽笛声的最高和最低频率相同．频率从最高到最低的连续变化过程发生在|x|

3 结论

驶过静止观察者身边的火车汽笛声的音调由最高到最低，经过观察者附近时有一段连续的降调过程．观察者离火车轨道越近，变调越快．

本文只分析了静止观察者接收到的火车汽笛声的音调变化，对运动的观察者,如在汽车中的观察者所听到火车汽笛声的音调变化可以用相同的方法来定量分析．

参考文献

1 吴王杰.大学物理学(下册).北京：高等教育出版社，2009.45