GPS天线相位中心改正及其影响分析

刘慧娟，党亚民，王潜心

（1.中国测绘科学研究院，北京 100830；2.山东科技大学，山东 青岛 266510）

1 引言

GPS天线相位中心改正通常可分为两个部分：天线相位中心偏差（PCO，Phase Center Offset）和天线相位中心变化（PCV，Phase Center Variation）。天线相位中心偏差指的是天线平均相位中心（天线瞬时相位中心的平均值）与天线参考点（ARP，Antenna Reference Point）之间的偏差；而天线相位中心变化指的是天线瞬时相位中心与平均相位中心的差值［1］。对于某一天线而言，PCO可以看成是一个固定的偏差量，而PCV则与信号方向有关，会随着信号的方位角及天顶角（天底角）的变化而变化。对于高精度的GPS定位，不仅要考虑天线相位中心偏差、天线相位中心变化，还要考虑GPS接收机整流罩对天线相位中心的影响以及不同频率天线相位中心的不统一等。

本文结合绝对天线相位中心模型，实现了GPS天线相位中心改化算法，用中国测绘科学研究院自主研发的GPAS软件进行实验数据解算，比较分析天线相位中心改正对基线解算结果的影响。

2 GPS天线相位中心改化原理

在外业测量中，能够直接得到的是地面标石到天线参考点或者天线盘面上某些可量测到的几何点之间的垂高或斜高。因此，在GPS数据处理时，首先需要将这个高度改化为瞬时相位中心与地面标石间的距离。

地面标石到瞬时相位中心的高度改化分为三部分［2］

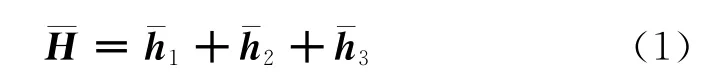
式中，是地面标石到天线参考点ARP之间的高度，是天线参考点到平均相位中心的偏移，即天线相位中心偏移PCO，是瞬时相位中心相对于平均相位中心的相位中心变化PCV。

IGS以 ANTEX（antenna exchange format）格式文件提供各卫星和各种不同型号接收机天线相位中心改正信息。从2006年11月5日起（GPS周为1 400，年积日309），IGS开始采用绝对天线相位中心模型（IGS＿05）改正天线相位中心变化，并将其轨道参数调整为IGS05模型。该模型既考虑了天线相位中心的偏差，也考虑了天线相位中心的变化，并考虑了天线整流罩的影响［3］。

GPS绝对天线相位中心改正模型的具体改正公式为［4］

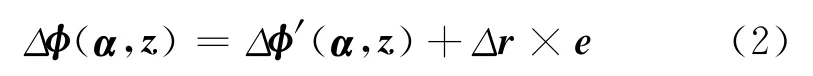
式中，α为卫星信号的方位角，z表示GPS接收机的天顶角或者GPS卫星的天底角（nadir angle），Δφ（α，z）为α及z方向的总的天线相位中心改正量，Δr表示平均天线相位中心至天线参考点（antenna reference point）的距离，e定义了接收机－卫星方向上的一个旋转矩阵，Δφ′（α，z）表示天线相位中心变化的改正值。

GPS卫星的改正信息通过十多年的IGS观测数据，并对GFZ和TUM计算结果取平均得到。具体改正方法是：卫星天线相位中心Z方向偏差改正按照单个卫星（satellite－specific）分类，X、Y方向改正按照同类卫星（block－specific）分类；天线相位中心变化改正按照同类卫星分类[5]GLONASS卫星的改正信息是由欧洲定轨中心（the Center for Orbit Determination in Europe，CODE）通过处理一年以上的数据来提供的。表1为igs05.atx文件所列的卫星天线类型。

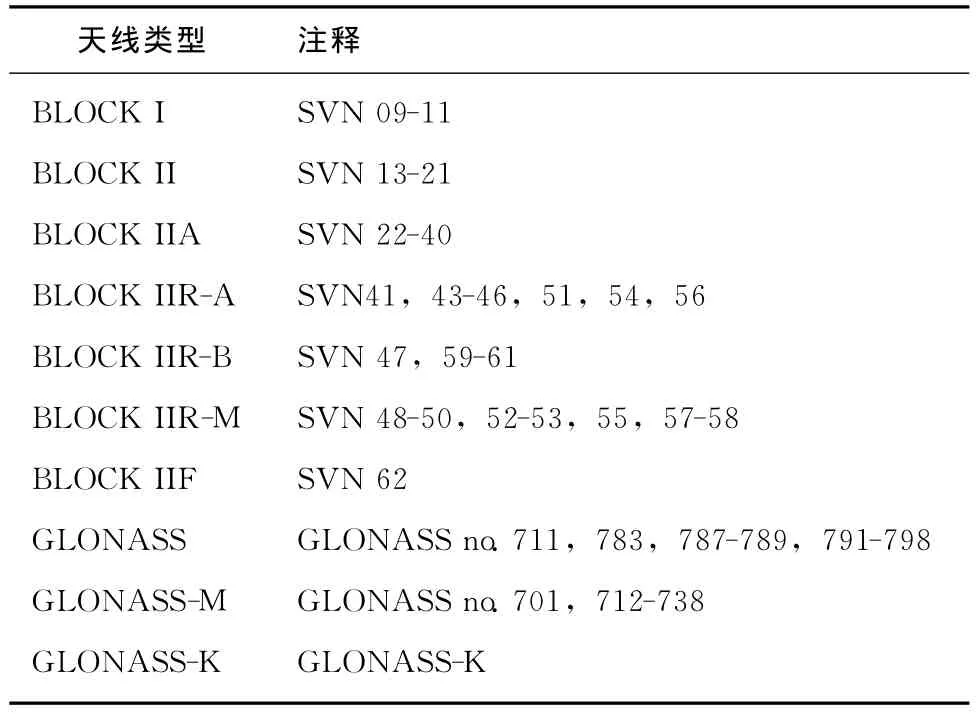
表1 igs05.atx文件所列的卫星天线类型［6］

2.1 相位中心的偏移

IGS提供的各卫星天线平均相位中心偏差直接以星固系下的坐标表示，而接收机的天线相位中心偏差在以天线参考点为原点的局部站心坐标系下给出。图1中G01表示L1频率；G02表示L2频率；NORTH／EAST／UP栏为PCO改正信息。同一类卫星L1、L2上的PCO改正信息是一样的，不同型号接收机的PCO改正信息是不一样的，对于同一型号接收机，其L1、L2上的PCO改正信息也是不一样的。

图1 天底角示意图

为计算经PCO改正后的卫星位置，设由卫星指向太阳方向的单位向量e为

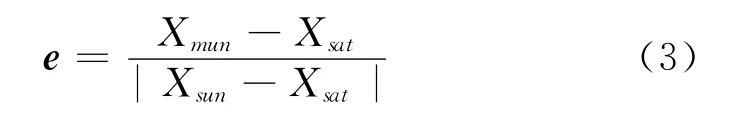
式中，Xsat是卫星质量中心在ECEF系中的坐标，可由精密星历获得；Xsun是太阳坐标。星固系的原点在卫星质心，Z轴指向地球质心，其单位向量ez为

星固系的Y轴是沿着卫星方向（卫星太阳能帆板方向）与太阳方向至卫星方向的向量积，其单位向量ex为

星固系X轴与另外两轴组成右手系，其单位向量ex为

卫星天线平均相位中心偏差改正为

接收机天线相位中心偏差改计算过程类似，既先将站心坐标系下的PCO转换为地固系下的改正量，再用式（2）来计算总改正量。

2.2 天线平均相位中心变化

IGS提供的卫星天线平均相位中心变化信息是一组随GPS卫星天底角（nadir angle）变化而变化的一组改正量，图1中NOAZI行。数据后处理时，可直接将改正量施加到L1、L2载波上。值得指出，与平均相位中心偏移量相同，在目前的ANTEX文件igs05.atx中，L1、L2上的PCV改正信息也是一样的。

如图1，天底角由0－14变化，间隔为1。用户根据所在位置的天底角，即可用线性内插的方法，利用两个最靠近的值，内插出特定天底角的PCV改正值，进而改正L1、L2上的相位观测值。

在图1中，设用户A到卫星S的距离为R；地球半径为Rearth；卫星高度角为e；天底角为nadir。在三角形OAS中，由正弦定理

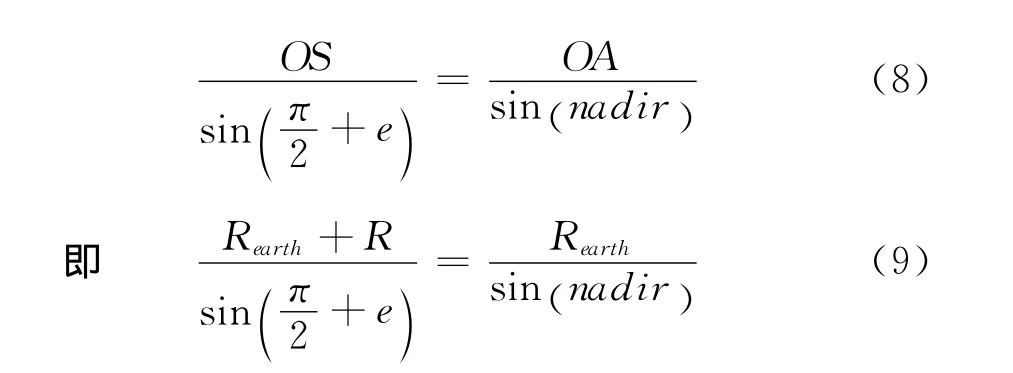
由式（9）求得天底角nadir，进而内插出相应的天线相位中心变化改正量。

接收机相位中心变化PCV采用两种形式给出，格式与图1中卫星改正信息类似。一种是只顾及卫星信号的天顶距而不考虑信号方位角变化时的天线相位中心变化（PCV NOAZI）；另一种是同时顾及卫星信号的天顶距及方位角时的天线相位中心变化（PCV AZEL）。目前，IGS是以5°的间隔给出接收机天线相位中心变化改正值的。因此，对于非格网点上的改正可以采用分段内插或者其他算法得到。

图2 方案一改正前后坐标分量偏差

3 计算实例分析

为比较有无天线相位中心改化对GPS定位测量的影响，本文采用2010年6月1日21个站点24h的观测数据，采用了TRIMBLE两种天线，其中一个为基准站，采用TRM 29659天线，其余20个站点接收机天线类型为TRM 55971。用中国测绘科学研究院自主研发的GPAS软件进行数据处理，以GAMIT解算结果作为坐标真值，用于实验结果的比较，设计了三种计算方案，实验方案及实验结果如下。

方案1：仅加入—地面标石到天线参考点ARP之间的高度的改正；

方案2：在方案一的基础上再加入天线相位中心偏移PCO的改正；

方案3：在方案二的基础上再加入天线相位中心变化PCV的改正。

图3 PCO改正前后与坐标真值的偏差

由图4可以看出，天线高改正对坐标三个分量的影响均在分米级，改正前后Y方向的偏差明显大于X、Z两个方向。

由图5可以看出，天线相位中心偏移PCO对坐标三个分量的影响均在厘米级，在方案一的基础上加入PCO改正后坐标与真值偏差在0刻度线附近1cm左右波动。在加入PCO改正前坐标三个分量与真值的差值均有系统性偏差，这是主要是天线相位中心偏差的影响，在天线类型相同时，通过双差可以减弱此项误差，但不能完全抵消。

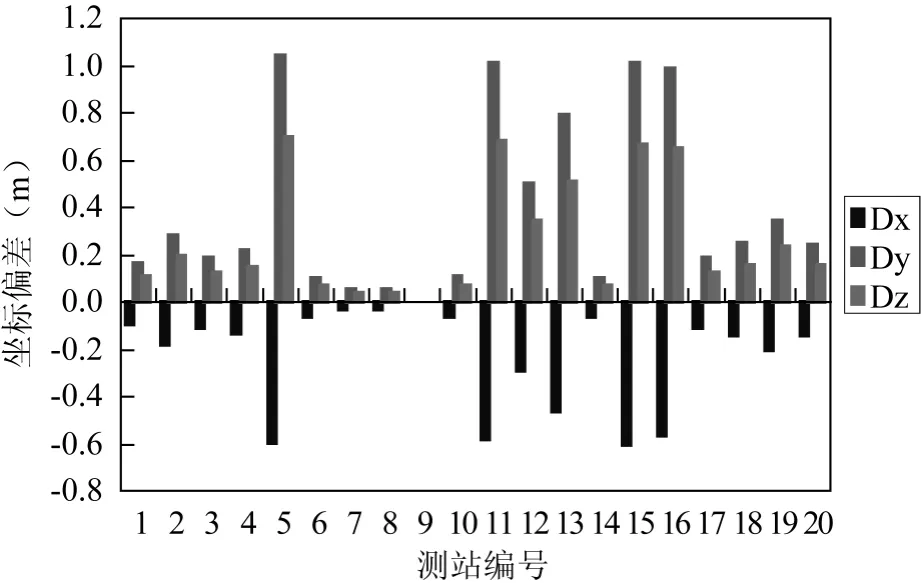
图4 PRN28号卫星的天线相位中心改正信息［6］

表2为改正前后点位坐标与GAMIT解算结果差值的统计，本文以GAMIT解算结果作为真值。从表中统计数据可以看出，天线高改正前后对坐标的影响在分米级，对Y方向的影响明显大于X、Z两个方向，方案1改正后点位精度X方向3cm左右，Y方向5cm左右、Z方向3.5cm左右。经方案2改正前后点位精度均在毫米级，X、Y、Z方向的平均精度分别为1mm、7mm、3mm左右。

方案3天线相位中心变化PCV改正的影响在毫米级，对坐标三个分量方向改正并无明显规律，文中未列出实验结果。

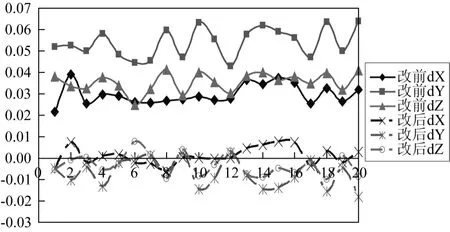
图5 TRM59800接收机的天线相位中心改正信息

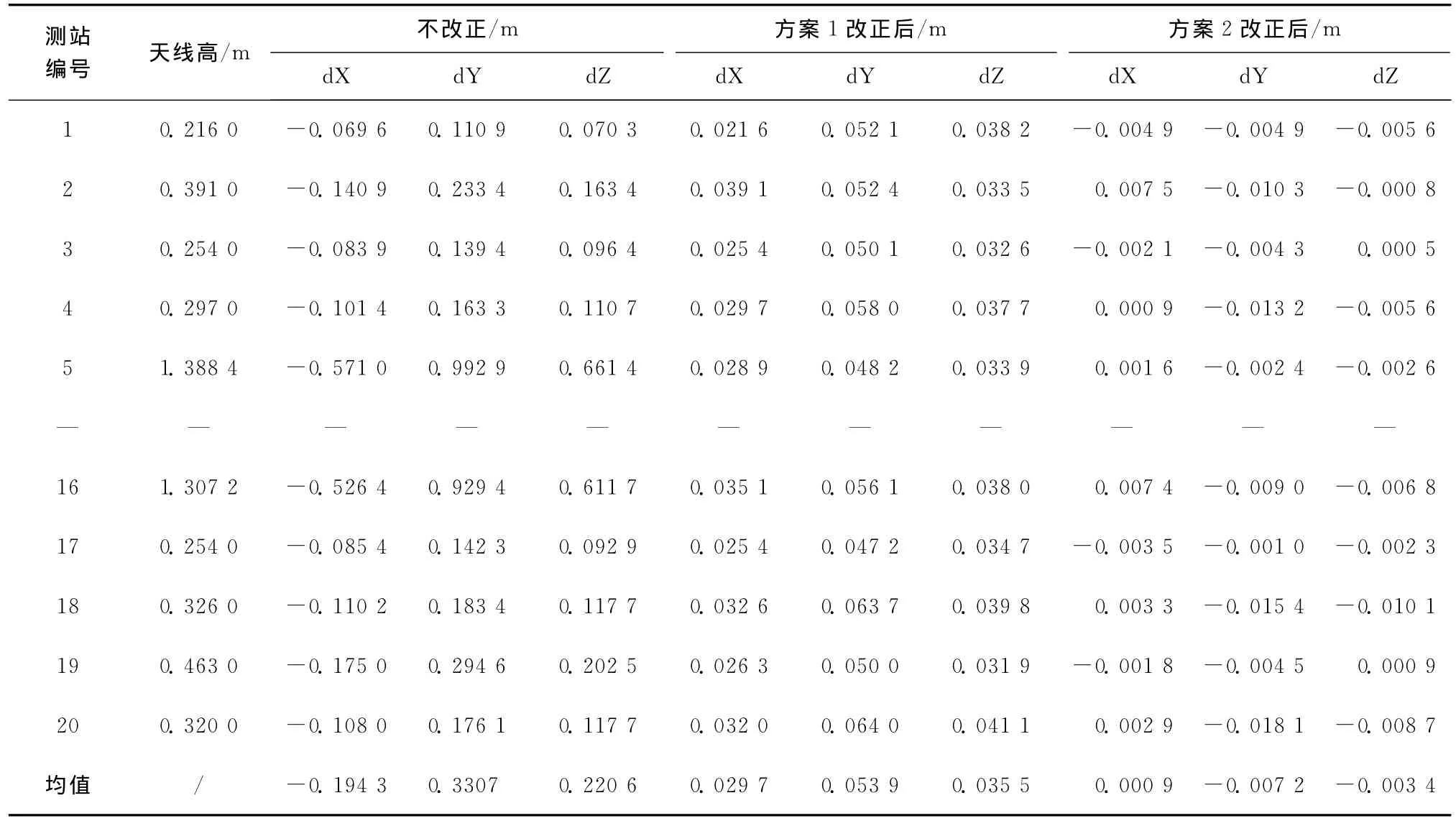
表2 方案1及方案2改正后点位精度统计表

4 结束语

本文结合绝对天线相位中心模型，实现了GPS天线相位中心改化算法，用中国测绘科学研究院自主研发的GPAS软件进行实验数据解算，比较分析了对基线解算结果的影响，实验结果表明：标石到天线参考点ARP之间的高度H的改正的影响最大，此项改正不可忽略。不论是长基线还是短基线，即使测量采用同种型号的天线，天线相位中心偏差PCO也无法完全抵消，应采用改正模型；在高精度测量数据处理时，应对天线相位中心变化进行改正，精度要求不高时此项改正可以忽略。

［1］ 李征航，黄劲松.GPS测量与数据处理［M］.北京：测绘出版社，2005.

［2］ 郭际明，史俊波，汪 伟.天线相位中心偏移和变化对高精度GPS数据处理的影响［J］.武汉大学学报：信息科学版，2007，32（12）：1143－1146.

［3］ HERRING T A，KING R W，MCCLUSKY S C.GAMI Reference Manual－GPS Analysis at MIT［EB／OL］.（2010－10－28）［2012－12－26］.http：／／www－gpsg.mit.edu／～simon／gtgk／GAMIT＿Ref.pdf.

［4］ DACH R，HUGENTOBLER U，FRIDEZ P，etal.Bernese GPS Software Version 5.0 ［EB／OL］.［2012－12－26］.http：／／www.bernese.unibe.ch／docs50／DOCU50.pdf.

［5］ 赵庆海.GNSS天线相位中心模型的演变［J］.全球定位系统，2011（5）：53－56.

［6］ ROTHACHER M，SCHMID R.ANTEX：The Antenna Exchange Format Version 1.3［EB／OL］.（2006－09－20）［2012－12－26］.http：／／igscb.jpl.nasa.gov／igscb／station／general／pcv＿archive／antex13.txt.

［7］ 陈绍杰，耿宏锁.GPS天线相位中心改正模型及其对的精度影响分析［J］.水资源与水工程学报，2010，21（5）：130－132.

［8］ 袁玉斌.GPS精密单点定位算法与大气延迟改正研究［D］.北京：中国测绘科学研究院，2010.

［9］ 张小红，李 盼，李星星，等.天线相位中心改正模型对参数估计的影响［J］.武汉大学学报：信息科学版，2011，36（12）：1470－1473.

［10］ 霍夫曼－韦伦霍夫B，利希特内格尔 H，瓦斯勒E.全球卫星导航系统：GPS，GLONASS，Galileo及其他系统［M］.程鹏飞，蔡艳辉，文汉江，等，译.北京：测绘出版社，2009.