适应于大气折射研究的压高公式

张捍卫，李爱国，2，丁安民

（1.河南理工大学 测绘学院，河南 焦作 454003；2.长安大学 地测学院，西安 710054）

1 引言

根据不同的观测技术，大气折射分为天文大气折射和大气折射延迟两个方向。天文大气折射是天文方位观测、天文导航、天文大地测量、时间和纬度服务的主要误差源之一。大气折射延迟是现代空间测量技术的主要误差源之一。大气折射研究不但能提高导航与定位的精度，而且在地球内部物理结构和动力学变化，大气和海洋变化的监测等科研、国民经济、国防领域上均具有重要现实意义［1］。地球大气的结构和性质是大气折射研究的理论基础，按热力学性质，大气分为对流层、平流层、中间层、热层和外逸层；按电磁特性，大气分为中性层、电离层和磁层［2］。对于目前的测量精度，天文大气折射只需考虑中性层的影响，而大气折射延迟还必须需考虑电离层的影响。大气折射研究主要有级数展开和映射函数方法两种，级数展开方法主要以文献 ［3－5］为代表；映射函数方法最初由文献 ［6］建立，并在其后得到了很大发展，例如文献 ［7－9］等。目前，大气折射研究已考虑到大气分布的方位性和时变性，例如文献 ［10－11］的工作。

在文献 ［3－5］和 ［12－13］的基础上，重新研究了大气折射理论中有关大气参数之间的理论关系和压高公式，指出对于大气折射研究来说，应该采用本文给出的压高公式，即式（11），以及水汽分压随温度变化关系式，即式（15）的第二式。

2 大气参数之间的理论关系

实验指出，在气体压力趋于零的极限条件下，对于给定质量的气体，其物态方程是［14］

式中，V、P和T分别是给定质量为M的气体所占据的体积、内部压力和热力学温度，μ是该气体的摩尔质量；＝8.314510J·mol－1·K－1是普适气体常数。

干大气和水汽的混合气体称为湿空气。以P、p和e分别表示湿空气的总大气压、干大气分压和水汽分压，根据道尔顿分压定律可知P＝p＋e。假设干大气和水汽是理想气体定律，则可知它们的物态方程分别是

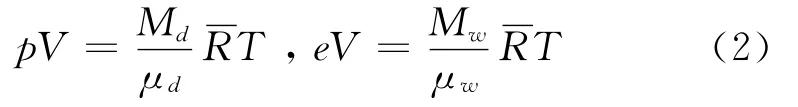
式中，下标d和w分别代表干洁大气和水汽有关的物理量。在大气包含375×10－6的二氧化碳成分条件下，文献 ［12］给出了干大气和水汽摩尔质量的数值为

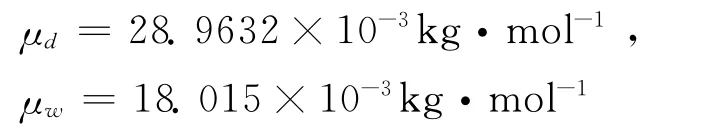
根据道尔顿分压定律以及式（2），可得以下两个等价的湿空气物态方程

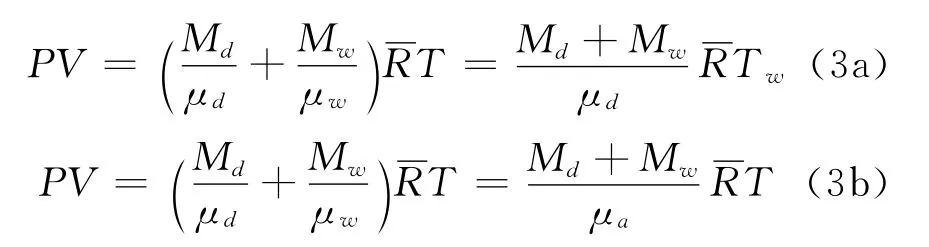
式中，μa称为湿空气的摩尔质量，Tw称为虚温度，它们的表达式是

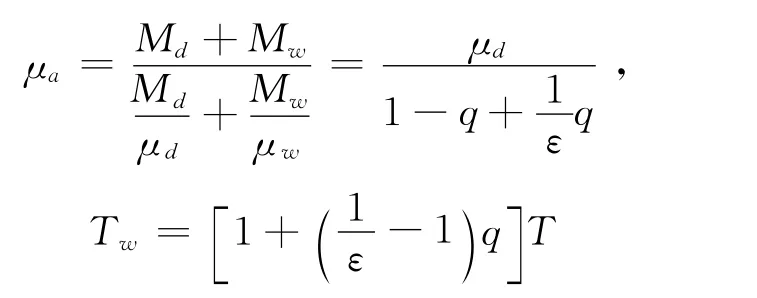
这里定义水汽与干大气的摩尔质量之比ε，以及湿空气的比湿q分别为

如果定义干大气、水汽和湿大气的比气体常数分别为

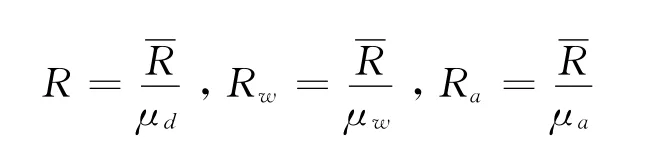
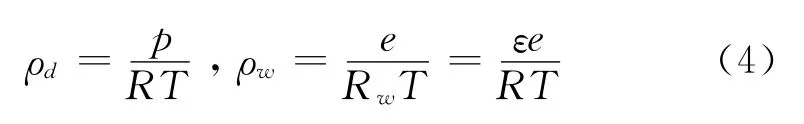
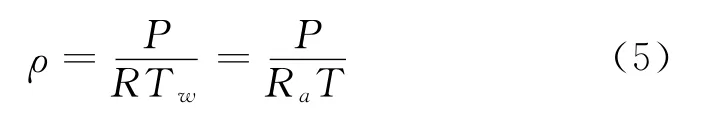
实际上，根据式（4）和ρ＝ρd＋ρw，也可得到式（5），只需证明下两式成立

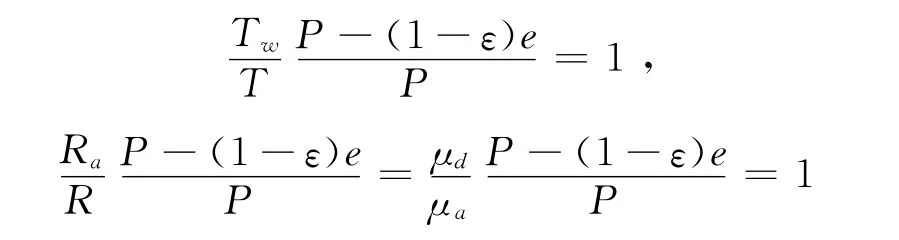
可见，采用虚温度Tw与采用 “湿大气比气体常数R′a”在描述湿大气密度时是等价的。

3 基于位势地心距的大气压高公式

假设地球大气是球对称分层分布的，也就是在一定范围内可认为干大气分压p和水汽分压e只与几何地心距有关系。干大气分压和水汽分压与几何地心距的微分关系是［12］：

式中，r表示几何地心距，g表示重力加速度。根据道尔顿分压定律和上两式，可得

利用式（4）和式（5），可把式（6）和式（7）写为

式中，除了干大气的比气体常数R和水汽与干大气的摩尔质量之比ε外，其余的参数都是几何地心距的函数，因此直接求上式的积分是很困难的。文献 ［13］根据气象学中位势高度的定义得到gdr＝g0dz，g0为测站重力值。因此采用位势高度后，式（8）变为

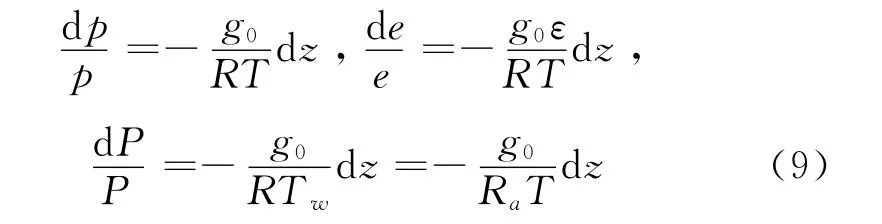
式（9）称为压高公式。采用位势高度的优势在于可只考虑温度随位势高度的分布，而不需要考虑重力加速度随高度和纬度的变化。

大气温度随高度的分布很复杂，难以用函数关系表达，因此对式（9）直接求积分几乎是不可能的。为此，需对温度的垂直分布作一些假设。

3.1 等温大气

若大气层的温度不随高度变化，由式（9）可得等温大气的压高公式为

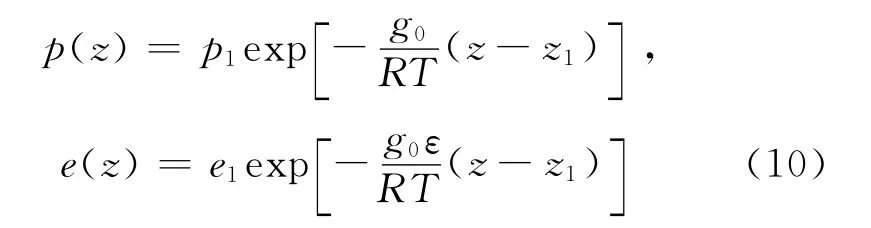
式中，p1和e1分别是位势高度为z1处的干大气分压和水汽分压。根据虚温度Tw和 “湿大气比气体常数R′a”的定义可知，Tw和Ra是湿空气比湿q的函数，而q对于某地区来说是随时间和高度变化的，因此不能直接对式（9）的第三个公式求积分。下面根据Tw的定义，来求式（9）的第三个公式的积分，即

因此，可得

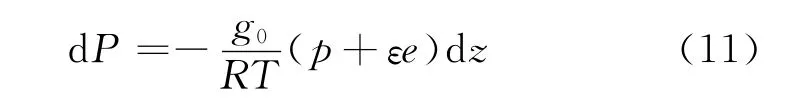
本文认为上式就是湿大气的压高公式。把式（10）的两个公式代入上式，又可得

对上式求积分可得

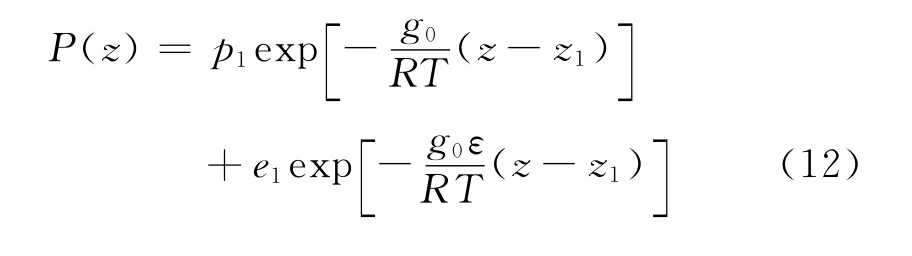
实际上，上式就是式（10 中两个式子的相加。

3.2 多元大气

多元大气是指气温是r或z的线性函数的大气层，即

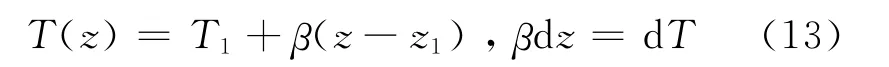
式中，T1是位势高度为z1处的温度。将上式代入式（9）前两个公式积分后，可得

或者

同理，由于Tw和Ra是q的函数，而q又是时间和高度z的函数，因此不能直接对式（9）的第三个公式求积分。利用式（11）和βdz＝dT，并把式（15）代入后有

对上式求积分可得

实际上，上式就是式（15）中两个式子的相加。

另外，根据式（15）可知

若海平面以上整层都是多元大气，由上式得到多元大气的上界（p＝0处）为

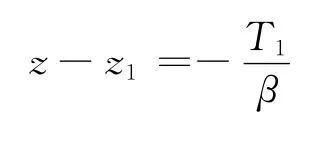
可见，多元大气是有上界的。多元大气的一个特例是等温大气（β→0），则可得上式右端趋近于无穷大，即等温大气没有上界。

3.3 讨论与分析

引入位势高度（地心距）概念后，使得对压高公式的积分中，不需要考虑重力加速度随高度和纬度的变化。这样既考虑到不同纬度的特性，也避免了把重力加速度在全球作为有效常数所带来的误差。同时，引入的虚温度更适合对大气折射问题的研究。

本文给出了湿大气的压高公式，即式（11）。基于此，式（10）与式（12），以及式（15）和式（16）是自洽的。因此，本文认为式（15）的第二个公式是正确的，而不是文献 ［3－5］以ν＝4代替ε＝0.622的情况。

文献 ［3－5］和 ［12－13］只讨论总大气压与几何地心距的关系，即式（8）的第三式，在讨论实际问题时，则认为Tw＝T或Ra＝R，这实际上就是干大气的压高公式。对于大气折射理论研究来说，这显然是不够完备的，因为还必须知道水汽的压高公式。

4 结论

基于文献 ［2］对于大气分层结构和美国标准大气模型的论述，可知等温层距离地表面11km以上，此层上部几乎没有水汽，这样在大气折射研究中，只存在式（10）的第一个公式。

大气层底部的多元层，既有干大气又有水汽，因此式（15）的两个公式都要用到；平流层和中层内部无水汽，则只存在式（15）的第一个公式。

以上给出的只是理论模型，由于不同地区上空大气分布的复杂性，在实际应用中需要长期的大气探测资料来拟合指数的数值。

［1］ 严豪健，符 养，洪振杰.现代大气折射引论［M］，上海：上海科技教育出版社，2006.

［2］ 中国大百科全书编辑委员会.中国大百科全书—大气科学卷［M］.北京：中国大百科全书出版社，1987.

［3］ SAASTAMOINEN J.Contributions to the Theory of Atmospheric Refraction［J］.Bulletin Géodésique，1972，105（1）：279－299.

［4］ SAASTAMOINEN J.Introduction to Practical Computation of Astronomical Refraction［J］，Bulletin Géodésique，1972，106（1）：383－397.

［5］ SAASTAMOINEN J.Contributions to the Theory of Atmospheric Refraction［J］.Bulletin Géodésique，1973，107（1）：13－34.

［6］ MARINI J W.Correction of Satellite Tracking Data for an Arbitrary Troposphere Profile［J］.Radio Science，1972，7（2）：223－231.

［7］ MENDES V B，LANGLEY R B.An Analysis of High－accuracy Tropospheric Delay Mapping Functions［J］.Physics and Chemistry of the Earth Part A，2000，25（12）：809－812.

［8］ BOEHM J，NIELL A，TREGONING P，etal.Global Mapping Function（GMF）：A New Empirical Mapping Function Based on Numerical Weather Model Data［J］.Geophysical Research Letters，2006，33（7）：1－4.

［9］ KOUBA J.Testing of Global Pressure／Temperature（GPT）Model and Global Mapping Function（GMF）in GPS Analyses［J］.Journal of Geodesy，2009，83（3－4）：199－208.

［10］ BERTON R PH.Variational Calculation of Three－dimensional Atmospheric Refraction：I.Description and Validation of the Method［J］.Journal of Optics A：Pure and Applied Optics，2006，8（A10）：817－830.

［11］ BERTON R PH.Variational Calculation of Three－dimensional Atmospheric Refraction：II.Application to Assessment of Positioning Accuracy［J］.Journal of Optics A：Pure and Applied Optics，2007，9（A7）：603－620.

［12］ 盛裴轩，毛节泰，李建国，等.大气物理学［M］.北京：北京大学出版社，2003.

［13］ 李爱国，丁安民，雷伟伟.蒙气差理论中的大气参数研究，测绘科学，2011，36（S1）：32－34.

［14］ 汪志诚.热力学与统计物理学［M］.北京：高等教育出版社，1980.