海洋潮汐及其参数选取方法对GPS基线解算精度的影响分析

赵文娇，党亚民，成英燕，宿 亮，李 兵

（1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.中国测绘科学研究院，北京 100830）

1 引言

由于受日月等天体引潮力的影响，海洋会产生潮汐现象，促使海水质量重分布，从而产生海洋潮汐的附加位。这一附加位的变化可引起地面测站变形，尤其是近海地区，这种形变在垂直方向可达到厘米级［1－2］。因此，海洋潮汐是GPS基线解算重要的误差源之一。针对这一误差，学者提出来多种海洋潮汐模型。目前，国际上的海潮模型 主 要 有 Schwiderski、GOT00.2、FES2004、CSR4.0、TRX0.7.2、NA099.b等十多种。在实际运用中，用户应选择精度较高且符合测区的最优模型，在此基础上再进行相关的解算和试验。

2 全球海洋潮汐模型

最早的海潮模型（如Schwiderski模型）是利用沿海验潮资料基于流体力学模型建立的。随着测高卫星的成功应用，获得了精确的水面抵消观测数据，也为海潮模型研究奠定了基础。

目前国际上的海潮模型主要有Schwiderski、GOT00.2、 FES2004、 CSR4.0、 TRX0.7.2、NA099.b等十多种，各个模型精度相当，且各具优势。NA099.b是日本国家天文台基于二维非线性浅水方程，并采用Blending方法综合（日本和韩国）沿海验潮站以及5年T／P沿轨海面高数据后建立的全球以及日本周边局部海潮模型［3］；CSR4.0是美国Texas大学的Richard等基于FES94.1动力学模型基础上，并对其进行长波长修正建立的，该模型保持了长波长的精度，又保留了FES94.1的空间分辨率［4］；GOT00.2模型也是基于 FES94.1动力学模型，并对其长波长进行修正，同时吸收了TOPEX／Poseidon卫星测高数据，在极地地区还综合了ERS1／2卫星测高数据而建立的，它还包含了多个区域海潮模型［4］；FES2004是 FTG（the French tidal group）推出的一系列有限元海洋潮汐模型的最新版本，它基于潮汐流体动力学方程，并融合了671个验潮站的数据、337个T／P和1254个ERS的测高数据［5］。

研究海洋潮汐，首先要了解的是海潮高。海潮的起落非常复杂，其根本来源是月亮和太阳，根据Farrell理论，由海潮的瞬时潮高与格林函数褶积积分算得海潮负荷。采用格林函数解法，可得到海潮负荷各个方向变化为［7］

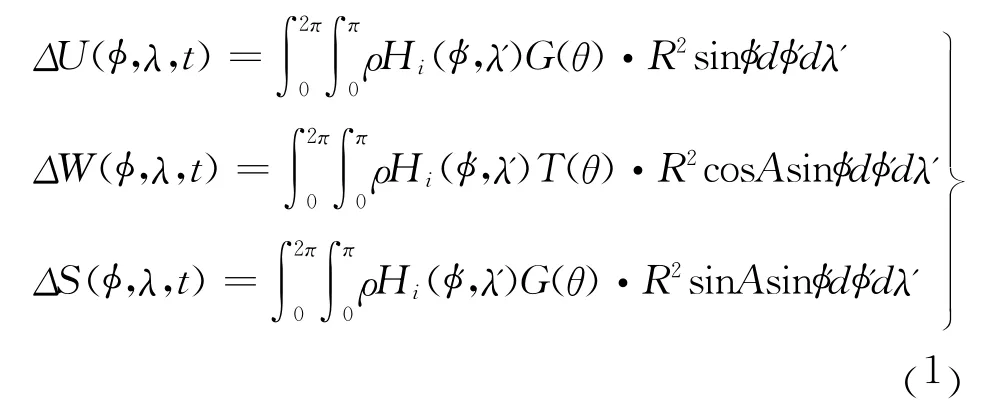
式中，ΔU、ΔW、ΔS分别为t时刻海潮负荷产生的测站U向、W向、S向的位移，ρ为海水密度，Hi（φ＇，λ＇）为积分面元第i个分潮波的瞬时潮高，φ、φ＇为测站积分面元纬度，λ、λ＇为测站积分面元经度，A为测站到积分面元方位角，θ为球面角，Δ（φ，λ，t）为测站的位移负荷。以此为基础可求出各分潮波位移改正的振幅与相位，进而求出测站的位移负荷变形

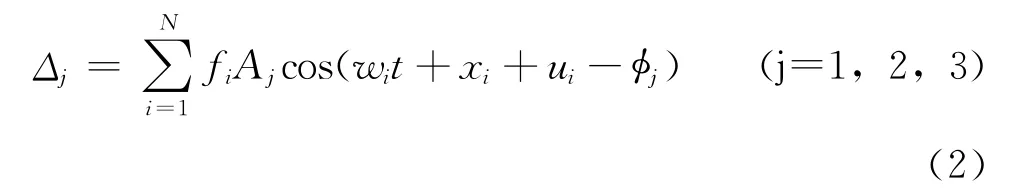
式中，Δj（j＝1，2，3）分别为测站S向、W向、U向海潮负荷变形，N为潮波总数，fi为与月球升交点经度相关的系数，Aj为与测站第j个位移分量相适应的第i个分潮波的振幅，wit＋xi＋ui为第i个分潮波在t时刻地球固体潮而造成的相位延迟，φj为格林尼治相位。由此可以看出位移变化与海潮模型关系密切，因而进行海潮改正时要求合理选择海潮模型，特别是符合测区的海潮模型。

研究发现，NA099.b模型在日本及我国沿海的符合性较好，但在全球范围内，FES2004模型相对其他模型而言更具优势［6－7］。考虑到本文是基于全球范围内的多个区域的站点进行试验和分析，故选取FES2004模型。

3 海洋潮汐对基线解的影响

海洋潮汐的模型改正直接在GPS数据处理软件中完成非常困难。GAMIT采用的方法是直接从文件otl.list中读取或通过全球范围的格网表otl.grid内插得到测站分潮波的振幅和相位即海潮系数。在具体操作中，测站如果距otl.list中某个跟踪站的距离小于10km，则测站的海潮系数就直接取用这个跟踪站的，否则就需要通过otl.grid内插［8］。

3.1 试验方案

为了能够真实有效的反应海洋潮汐对基线解算精度的影响，并考虑到数据处理的工作量问题，本文选取了大洋洲、南非、南美、北美、西欧、亚洲和南极洲七个区域2010年8月5日的数据，运用GAMIT软件进行解算。同时，为了最大程度地减小其他误差源对本试验的干扰，设计了如下最优的数据处理方案：采用IGS的最终精密星历，设定卫星截止高度角为15°。连续观测时间为24h。采用saast amoinen对流层改正模型和WMF1对流层映射函数，以2h为时间间隔分段线性估计测站处的对流层延迟。加载全球气温气压模型GPT、大洋潮改正模型FES2004，依照IERS2003规范进行地球固体潮和极潮改正［9］。以下各方案均基于此设置进行。

方案一：不加载海洋潮汐参数；

方案二：加载海洋潮汐参数 （同时加载grid.olt和list.otl）。

3.2 试验结果分析

根据以上试验方案，最终得出各组站点间的基线受海洋潮汐影响的误差统计如表1所示。

由表1分析可以发现，北美洲受海洋潮汐影响最为明显，南非则影响最小。其中南北方向上最大误差达到了9.95mm，东西向误差最大达到了5.40mm，高程方向误差最大达到了9.63mm。且高程方向的平均误差普遍大于南北方向和东西方向，说明海洋潮汐对站点的影响主要体现在高程方向上。

表1 基线解受海洋潮汐影响误差统计表／mm

为比较距海远近不同站点（见图1）的海潮对基线解的影响，作者选取了站点分布均匀且误差中等的亚洲地区为作进一步分析。亚洲地区的解算结果如表2及图2所示。

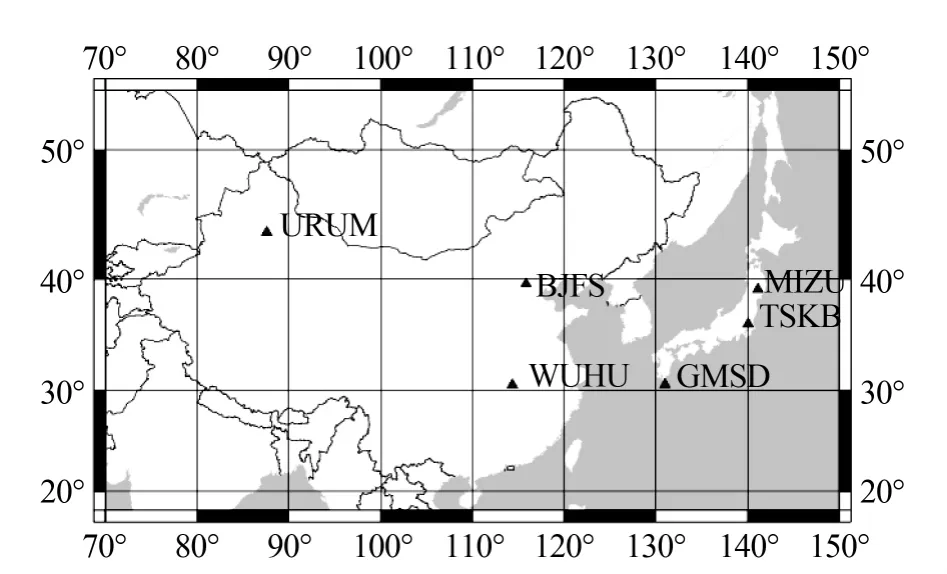
图1 亚洲地区站点分布图

表2 亚洲区域站点受海洋潮汐影响高程方向误差统计表

结合表2及图2可以看出，在亚洲区域内，海洋潮汐对单个点位的影响达到了厘米级，且沿海点的误差均大于内陆点。其对基线的影响，虽然在U方向误差较大近1mm，但对基线长的影响一般较小。而且海潮对内陆点－内陆点组合以及沿海点－沿海点的组合的基线影响较小，对内陆点－沿海点组合如 MIZU－URUM 和 TSKB－URUM，其基线长受海潮影响的误差就略大些。

4 不同海洋潮汐参数选取方法对比研究

4.1 试验方案

图2 亚洲区域基线各方向受海洋潮汐影响误差图

对表1进行分析可发现，大洋洲受海潮影响较为明显，原因是其四面环海，站点只有一个点位于内陆，其余站点全部位于沿海，如图3所示。大洋洲各站点均可在list.otl中找到相应的海潮参数，因此可利用大洋洲区域的站点来比较其加载list.otl和grid.otl对基线解的不同影响。

图3 大洋洲地区的站点分布图

方案一：加载list.otl。

方案二：加载grid.otl。

4.2 试验结果分析

根据以上试验方案，得到结果见表3、图4。

表3 大洋洲区域站点基线长受海洋潮汐不同参数选取方法影响误差统计表

图4 大洋洲区域站点基线长受海潮参数选取方法影响误差图

由表3和图4中可知，当站点由list.otl和grid.otl均可得到相应的海潮参数时，加载list.otl得出基线解的精度略高于加载grid.otl，但其差距较小，均小于0.2mm，基本可忽略。经对比发现，只加载list.otl得到的海洋潮汐参数U文件与同时加载list.otl和grid.otl文件得到的几乎完全一样，其原因是大洋洲各站点的海潮参数均可在list.otl文件中找到，系统自动选取了这些参数。

在实际测量和解算中，并不是所有点都可在list.otl中找到相应的海潮参数，此时就需要用到grid.otl。故实际解算中最好是选择otl.list＝Y且otl.grid＝Y。系统可自动在otl.list中抽取站点的潮汐参数，未能找到的即为其加载otl.grid，以求获得高精度的基线解。此外，如果地方测站与IGS测站距离很近，建议用格网文件，这样就不用在两个测站的运动中人为加入相关性了。

5 结束语

通过以上对7个主要区域的GPS网数据的基线处理结果所进行的分析可以得出如下结论：7个区域中，海洋潮汐对南非的影响最小，对北美洲影响最大。在其他区域，对基线长的影响可达4.86mm的误差。且距海较近的点误差较大，导致包含近海点的基线误差也偏大。而格网法和站就近法对基线解的影响差别微小，基本可以忽略，实际运用中建议两者结合使用。

［1］ 许大欣.GPS测站的海洋潮汐改正［J］.地壳形变与地震，1998，18（3）：32－35.

［2］ 郑 祎，伍吉仓，王解先，等.GPS精密定位中的海潮位移改正［J］.武汉大学学报：信息科学版，28（4）：405－421.

［3］ MATSUMOTO K，TAKANEZAWA T，OOE M.Ocean Tide Models Developed by Assimilating Topex／Poseidon Altimeter Data into Hydrodynamical Model：A Global Model and a Regional Model around Japan［J］.Journal of Oceanography，2000，56（5）：567－581.

［4］ 刘 立.负载潮对我国沿海地区精密定位的影响研究［D］.北京：中国测绘科学研究院，2011.

［5］ LYARD F，LEFEVRE F.Thierry Letellier and Olivier Francis Modelling the Global Ocean Tides：Modern Insights from FES2004［J］.Ocean Dynamics，2006，56（5－6）：394－415.

［6］ 李大炜，李建成，金涛勇，等.利用验潮站资料评估全球海潮模型的精度［J］.大地测量与地球动力学，2012，32（4）：106－110.

［7］ 董春来，蒋廷臣，周 立.基于JSCORS的全球海潮模型比较研究［J］.测绘通报，2012（8）：1－3.

［8］ Massachusetts Institute of Technology.Documentation for the GAMIT GPS Analysis Software［EB／OL］.［2012－12－25］http：／／www－gpsg.mit.edu／～simon／gtgk／GAMIT.pdf.

［9］ 邹 璇，姜卫平.潮汐改正对精密 GPS基线解算的影响［J］.测绘信息与工程，2008，33（1）：6－8.