Kruskal-Wallis秩和检验及其应用*
田 兵
(包头师范学院 《阴山学刊》编辑部,内蒙古 包头 014030)
方差分析是研究一种或多种因素的变化对实验结果的观测值是否有显著影响,从而找出较优的试验条件或生产条件的一种常用数理统计的方法.其被广泛的应用到社会各个领域.方差分析过程需要满足若干条件F检验才能进行.但是在实际研究工作中,观测得到的数据往往不能满足这些条件.
在现实的研究中,我们遇到的数据常常具备以下特点:
(1)数据的总体分布类型未知;或
(2)数据的总体分布类型已知,但不符合正态分布;或
(3)某些变量可能无法精确测量.
对于类似的数据,除了将数据进行变量替换或者是t检验以外,还可以使用非参数统计方法.参数统计是总体分布类型已知,用样本值来对总体参数进行估计或者是做出假设检验的统计方法.非参数统计是抛开总体分布类型不考虑,对总体参数不做比较,比较的是总体分布的位置是否相同的统计方法.秩和检验是非参数统计中一种经常使用的检验方法.这里的“秩”又可被称为等级,即按照数据大小排定的次序号.此次序号的总和被称为“秩和”.如果将所观测的数据转化为秩统计量,由于秩统计量的分布与总体分布无关,这样就可以避开总体分布的要求.上述问题就可以通过数据的秩统计量就解决了.
在比较两个以上的总体时经常使用Kruskal-Wallis秩和检验,它是对于两个以上样本进行比较的非参数检验方法.
1 Kruskal-Wallis秩和检验

Ri1,Ri2,…,Rini,i=1,2,…,m,
假设观测值中无结点,即Ri1 H0:各处理方法的效果无显著差异 能否接受. 为了构造合适的检验统计量,只有原假设是不够的,还应对相应的备择假设有足够的了解.Kruskal-Wallis秩和检验考虑的是最常见的一种备择假设,即各方法的处理效果如果有差异,其差异主要反映在各组个体处理效果的度量值的分离上.也就是说,如果这些方法的实际效果有明显的区别,那么接受各种方法试验的个体的秩之间有一个排序,其中某些方法中个体的秩趋于取较小值,另一些方法中个体的秩趋于取较大的值.下面针对此类备择假设构造检验统计量.令 其中Ri·是第i组个体的秩的平均值(i=1,2,…,m),R··是总的平均值.如果这些方法的实际效果之间有明显的区别,按上述备择假设,则Ri·(i=1,2,…,m)相互差异较大.反之,若H0为真,由于分组时是随机的,则各Ri·(i=1,2,…,m)差异应较小,且都分散在R··附近.因此,可以用(Ri·-R··)2的加权来度量各Ei·与R··的接近程度.令 称K为Kruskal-Wallis统计量.若H0不真,则K有偏大的趋势.因此,其拒绝域形式为 K≥c 或者计算出相应的P值.当P值小于相应的显著性水平,则拒绝原假设.上述检验方法称为Kruskal-Wallis秩和检验. (1)等级数据. (2)偏态分布数据.当观察得到的数据表现出明显的偏态分布却没有作变量变换,或变量变换后依旧未达到正态或近似正态分布,比较两个以上的总体时宜用Kruskal-Wallis秩和检验. 公司背靠万达商业,跨区域开发能力突出,兼具高流量和低成本优势。大部分依托于万达商业地产,选址风险和租金成本均低于行业平均。随着万达商业在三四线城市加速下沉,公司有望在三四线市场提高影响力。公司票房市占稳定在13-15%,领先的放映技术和观影体验带来高票价,NOC系统和大数据分析助力科学排片,提升上座率。随着行业扩张回归理性、中小院线出清,经营效率高的龙头有望提升盈利能力和市场占有率。 (3)方差不齐,且不能通过变量变换达到齐性. (4)个体数据偏离过大,一端或两端无界的数据. (5)分布类型不明. (1)对样本所来自的总体分布形式没有要求,不受总体分布限制,适用面广. (2)收集资料方便,可用“等级”或“符号”来记录观察结果. (3)操作比较简便,易于理解、掌握,容易计算. (1)不能充分利用信息,检验效能低,适用于参数检验的资料用Kruskal-Wallis秩和检验会降低检验效能. (2)得出的是各总体分布不同或不全相同的结论.若要对每两个总体分布做出有无不同的推断,需要作组间的两两比较. (3)编秩时相同值要取平均秩次;相同秩次较多时,统计量要校正. 以小白鼠为对象研究正常肝核糖核酸(RNA)对癌细胞的生物作用,试验分别为对照组(生理盐水),水层RNA组和酚层RNA组,分别用此3种不同处理方法诱导肝癌细胞的果糖二磷酸酯(FDP酶)活力,数据如表1所示,那么3种不同处理的诱导作用是否相同? 表1 3种不同处理的诱导结果 解 根据题意,原假设 H0:试验中3种诱导作用的效果无显著差异,H1:试验中3种诱导作用的效果有显著差异. R软件提供了Kruskal-Wallis秩和检验,对应的函数为kruskal.test(),使用方法如下 kruskal.test(x,g,...) kruskal.test(formula,data,subset,na.action,...) 其中x是由数据构成的向量或者是列表;g是由因子构成的向量,当x是列表时,此项无效;formula是方差分析的公式;data是数据框. 我们根据R软件中的kruskal.test函数来解决这个问题. RNA<-data.frame( X=c(2.79,2.69,3.11,3.47,1.77,2.44,2.83,2.52, 3.83,3.15,4.70,3.97,2.03,2.87,3.65,5.09, 5.41,3.47,4.92,4.07,2.18,3.13,3.77,4.26), A=factor(rep(1:3,c(8,8,8))) ) kruskal.test(X~A,data=RNA) Kruskal-Wallis rank sum test data:X by A Kruskal-Wallis chi-squared=7.9322,df=2,p-value=0.01895 P=0.01895<0.05,H1为真,所以认为试验中3种诱导作用的效果有显著差异,3种诱导作用不同. 参考文献: [1]何书元.概率论与数理统计[M].北京:高等教育出版社,2006. [2]薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007. [3]王松桂,陈敏,陈立萍.线性统计模型[M].北京;高等教育出版社,1999. [4]黄水平.多样本资料的秩和比法与秩和检验的比较[J].中国卫生统计,2002(6). [5]孙国强,冯长焕.关于秩和检验的一点讨论[J].太原师范学院学报,2013(2). [6]王率滨.秩和检验的可靠性及其应用[J].统计与咨询,1994(4). [7]于长春.秩和检验-Kruskal-Wallis法和Nemenyi法在科室医疗质量动态监测中的应用[J].中国医院统计,2009(1). [8]王俊.实际应用中方差分析与秩和检验结果比较[J].中国卫生统计,2008(1).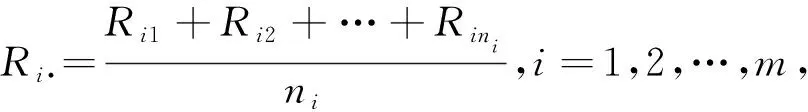
2 Kruskal-Wallis秩和检验的适用范围及其优缺点
2.1 适用范围
2.2 优点
2.3 缺点
3 实例


