Minkowski空间上平分集的道路连通性

许 晶,吴晓微

(通化师范学院 数学学院,吉林 通化 134002)

1 预备知识

设X是一个Minkowski空间(即实有限维的赋范线性空间)，‖·‖是X上的范数．用ο表示X的原点，用SX={x:‖x‖=1}和BX={x:‖x‖≤1}分别表示X的单位球面和单位球．对任意不同的两点x,y∈X，用[x,y]表示以x,y为端点的线段，〈x,y〉表示过x,y两点的直线，[x,y〉表示以x为起点，过y点的射线．

设p,q∈X，p≠q，称集合

B(p,q)={x∈X:‖x-p‖=‖x-q‖}

为p,q的平分集，也称B(p,q)是线段[p,q]的平分集．R.C.James给出了等腰正交的概念:设x.y∈X，若等式‖x+y‖=‖x-y‖成立，则称x等腰正交于y，记作x⊥Iy．

B(-x,x)={z:x⊥Iz}

这意味着等腰正交的性质决定了Minkowski空间平分集的几何结构，反之亦然．文献[3]得到的结果是从一个赋范线性空间X到另一个赋范线性空间Y的线性算子保持等腰正交的充要条件是它是一个线性等距的倍数．所以，可利用Minkowski空间平分集的几何性质来刻画特殊的赋范线性空间或深入的研究所在空间的几何性质，其几何结构也因此一直是人们关注的热点问题[4-9]．

设X是一个线性空间．称f是X中从x到y的一条道路时满足x=f(0)和y=f(1)，其中f(0)为道路的起点，f(1)为道路的终点．称集合A是道路连通的满足对于集合A中∀x,y，都存在A中的一条从x到y的道路．下证平分集是道路连通的．

2 主要结果

我们首先证明Minkowski平面上平分集是道路连通的，然后将该结果推广到维数d≥3的Minkowski空间中．

对∀x∈X，用M(x)表示平行于〈-x,x〉，并且包含在SX中的极大线段[a,b]的长度，如果不存在平行于〈-x,x〉且包含在SX中的线段[a,b]，我们令M(x)=0．

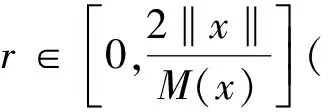
定理1 设X是一个Minkowski平面．对∀p,q∈X，B(p,q)是道路连通的．

我们由范数诱导的距离的平移不变性和范数的绝对齐次性，只需要证明对∀x∈SX，B(-x,x)是道路连通的。我们分两种情形来讨论:

令

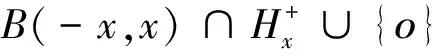
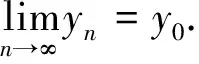
‖yn+x‖=‖yn-x‖

因此

‖y0+x‖=‖y0-x‖

即y0∈B(-x,x)．

再证f1(t)是连续的．如果不这样的话，存在一点t0∈+和一个序列{tn}⊂+符合使得或者不存在．不论哪一种情形，可得{f1(tn)}的一个收敛子序列{f1(tnk)}满足则

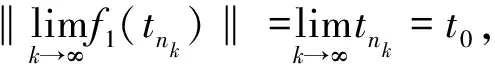
类似的，建立如下映射

f2:+→B(-x,x)

令

aλ=(1-λ)a+λb,bλ=(1-λ)b+λa,

所以存在一条射线

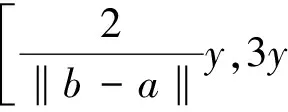
同理可得

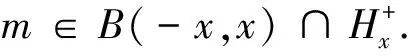
f:[0,1]→[m,p]
t→m+t(p-m)

显然f是连续的．一方面，我们有

对∀m,n∈B(-x,x)，存在一条连接m和ο的道路，同时存在一条连接n和o的道路，故存在一条连接m和n的道路．

定理2 设一个Minkowski空间X满足dimX≥3．对∀p,q∈X，B(p,q)是道路连通的．

证明 只需证明对∀x∈SX，B(-x,x)是道路连通的．对∀m∈B(-x,x){ο}，我们不妨令X1=span{x,m}．SX〗=X1∩SX。由定理1，可得存在一条连接m和ο的道路．对∀n∈B(-x,x){ο}，存在一条连接n和ο的道路．因此，对∀m,n∈B(-x,x)，存在一条连接m和n的道路．

参考文献：

[1]JAMES R C. Orthogonality in Normed Linear Spaces [J]. Duke Math. J,1945, 12: 291-301.

[2]AMIR D. Characterizations of Inner Product Spaces [M]. Basel: Birkhauser Verlag, 1986: 1-200.

[3]MARTINI H, WU SENLIN. On Maps Preserving Isosceles Orthogonality in Normed Linear Spaces [J]. Note Ma,2009, 29: 55-59.

[4]HORVATH A G. On Bisectors in Minkowski Normed Spaces [J]. Acta. Math. Hungar,2000, 89: 233-246.

[5]HOLUB J R. Rotundity Orthogonality and Characterizations of Inner Product Spaces [J]. Bull. Amer. Math. Soc,1975, 81: 1087-1089.

[6]MARTINI H, WU SENLIN. Radial Projections of Bisectors in Minkowski Spaces [J]. Extracta. Math, 2008, 23: 7-28.

[7]MARTINI H, SWANEPOEL K J. The Geometry of Minkowski Spaces-a Survey Part II [J]. Expositions Math, 2004, 22: 93-144.

[8]MARTINI H, SWANEPOEL K J. The Geometry of Minkowski Spaces-a Survey Part I [J]. Expositions Math, 2001, 19: 97-142.

[9]WU SENLIN. Geometry of Minkowski Planes and Space-Selected Topics [D]. Chemnitz: TU Chemnitz, 2009.

[10]JI DONGHAI, LI JINGYING, WU SENLIN. On the Uniqueness Property of Isosceles Orthogonality in Normed Linear Spaces [J]. Results in Mathematics, 2011,59: 157-162.