Clifford代数与时空平面的Lorentz变换
张淑娜
(通化师范学院 数学学院,吉林 通化 134002)
1 背景知识
Clifford代数Clp,q的生成空间Rp,q为(p,q)型Minkowski空间,对Rp,q的基元e1,…,ep,ep+1,…,ep+q定义Clifford积(亦称几何积),即可得到Clp,q的一组基
1
e1,…,ep,ep+1,…,ep+q
e1e2,…,e1ep+q,e2e3,…,e2ep+q,…,ep+q-1ep+q
…………
e1e2…ep+q.
我们熟知的实代数,复代数,四元数代数,Pauli代数与Dirac代数依次同构于Cl0,0,Cl0,1,Cl0,2,Cl3,0与Cl4,0.
1.1 Clifford代数的两种虚单位与两种平面复数

〈e1〉={a+be1|a,b∈R},
〈e2〉={a+be2|a,b∈R}
均为Cl1,1的二维子代数.令j≡e1,i≡e2,则
〈e1〉={a+be1|a,b∈R}≅H,
〈e2〉={a+be2|a,b∈R}≅C
依次称为双曲复数与椭圆复数.
1.2 时空平面的表述
时空平面(亦称Minkowski平面,简记为M平面)是带有Minkowski内积的2维实线性空间.下面给出Minkowski平面的四种表述方式.
例1 在复平面C={x=iy|x,y∈R,i2=-1}上引入M内积:
(x1+iy1)·(x2+iy2)=x1x2+iy1iy2
=x1x2-y1y2,
则C平面成为时空平面.
例2 在双曲复平面H={x+jy|x,y∈R,j2=1,j∉R}上引入M内积:
(x1+jy1)·(x2+jy2)=
x1x2+jy1(jy2)*=x1x2+jy1j*y2=x1x2-y1y2,
其中j*=-j称为双曲虚单位j的复共轭,则H平面成为时空平面.
例3 4维实Clifford代数Cl1,1的生成空间R1,1={xe1+ye2|x,y∈R},作为Cl1,1的2维子空间关于Cl1,1的内积:e1·e2=1,e2·e2=-1,e1·e2=e2·e1=0作成时空平面.
2 时空平面的双曲Euler公式
2.1 双曲复平面的双曲Euler公式
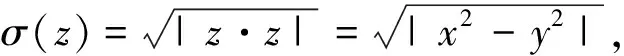
当σ(z)≠0时,定义向量的幅角φ为
φ=arctanh(sgn(xy)min{|x|,|y|}/
max(|x|,|y|)).
定义z的示向数为
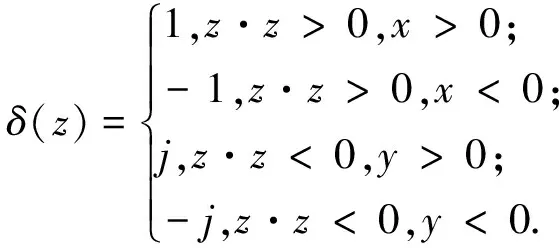
由此,z可表为指数形式及双曲函数形式
z=δ(z)σ(z)exp(jφ),
z=δ(z)σ(z)(coshφ+jsinhφ),
上式蕴含
exp(jφ)=coshφ+jsinhφ
(或记为ejφ=coshφ+jsinhφ),
称为H平面的双曲Euler公式.
2.2 Cl1,1偶子代数的双曲Euler公式

〈e1〉={a+be1|a,b∈R}≅〈e12〉=
{a+be12|a,b∈R}.
两者的不同之处是,Cl1,1的生成空间R1,1可以是偶子代数

ee12φ=coshφ+e12sinhφ
既可用于考察时空平面H的性质,也可用于考察时空平面R1,1的性质.
3 旋量群与Lorentz变换
3.1 Clifford群与旋量群
Clifford代数Clp,q的Clifford群(亦称Lipschitz群)定义为

它的子群
旋量群Spin(p,q)则是Pin(p,q)的子群
由如上定义可知,旋量群Spin(p,q)可用于考察Rp,q的性质.当p=q=1时,有
或
Spin(1,1)={x+ye12∈Cl1,1|x2-y2=±1}.
3.2 Spin+(1,1)与Lorentz变换

Spin(1,1)={x+ye12∈Cl1,1|σ(w)=1},
Spin+(1,1)={x+ye12∈Cl1,1|x2-y2=1},

Spin+(1,1)=
{±(coshφ+sinhφe12)∈Cl1,1|φ∈R},
或记为
Spin+(1,1)={δ(coshφ+sinhφe12)∈
Cl1,1|φ∈R,δ∈{1,-1}}.
类比于上式,也可利用双曲函数式将Spin(1,1)表为
Spin(1,1)={δ(coshφ+sinhφe12)
∈Cl1,1|φ∈R,δ∈{±1,±e12}}.

.

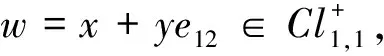
lu(w)=uw=δ(xcoshφ+ysinφ)+φ(ycoshφ+xsinφ)e12.
.
注意到
lu(w)·lu(w)=
(xcoshφ+ysinhφ)2-(ycoshφ+xsinhφ)2=
x2-y2=w·w.
可知lu为Lorentz变换.进一步验证可知,在L以变换的合成作为运算构成群,故L以变换的合成为运算构成Lorentz群.再由群L与群Spin+(1,1)同构可知,Spin+(1,1)也是Lorentz群.
参考文献:
[1]D.Hestenes.Space-Time algebra[M].NewYork:Gordon and Breach,1966.
[2]Lounesto P.Clifford algebra and spinors [M].Cambridge University Press,2003.
[3]李武明.Clifford代数与Minkowski空间的性质[J].吉林大学学报,2000(4).
[4]李武明.时空平面的Clifford代数与Abel复数系统[J].吉林大学自然科学学报,2007(5).

