PdI混合源剂量学参数的蒙特卡罗模拟

郑玉来，王 强，张为在

(中国原子能科学研究院，北京 102413)

放射性粒子源125I和103Pd广泛用于前列腺、眼睛等器官恶性肿瘤的永久性植入治疗[1-3]。最近，中国原子能研究院设计了一种新型的放射性近距离治疗用种子源，125I-103Pd混合源。临床使用该粒子源近距离治疗时，需要确定粒子源的剂量学参数。为此，利用蒙特卡罗方法对125I-103Pd混合源进行模拟计算，以确定粒子源的剂量学特征，包括剂量率常数、径向剂量函数和各项异性函数。

1 剂量计算参数

美国医用物理学家协会(american association of physicists in medicine，AAPM )在1995年发布了用于指导短程治疗源在组织中的剂量TG-43报告[4]，并于2004年发布其修订版TG-43U1。目前推荐的短程治疗源剂量计算公式[5]如下：

(1)

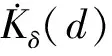
SK=Kδ(d)d2

(2)

SK的单位符号为cGy·h-1·cm2，专用符号为U，U=1 Gym2h-1=1 cGycm2h-1

∧为剂量率常数，表示液态水中参考点处单位空气比释动能强度的源所致剂量率，即：

(3)

∧的单位为cGy·h-1·U-1。定义中将液态水作为组织等效材料。

GL(r，θ)为几何函数。该函数是对适用于点源的反比平方定律的修正，其具体的计算公式如下：

(4)

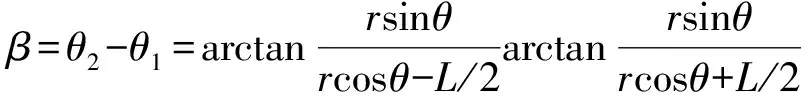
(5)

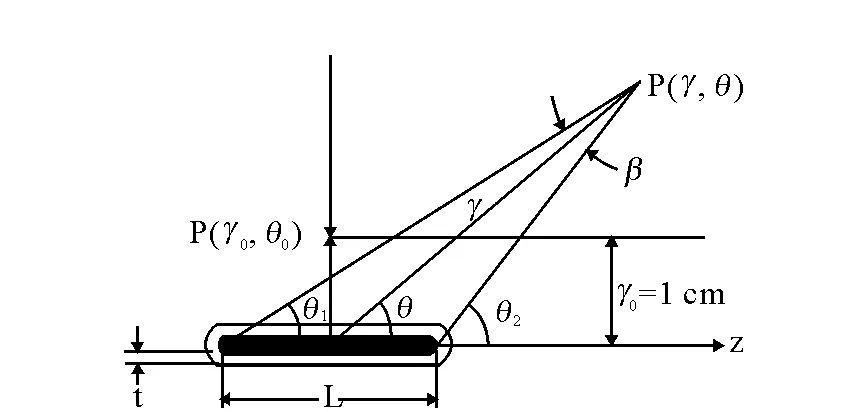
图1 近距治疗剂量计算坐标系Fig.1 Coordinate system used for brachytherapy dosimetry calculation

g(r)为径向剂量函数，用于对种子源中垂轴不同距离处组织(液态水)的衰减和吸收进行修正，其计算公式为：

(6)

g(r)是一相对比值，即在中垂轴上对参考点进行归一。于是，g(r0)=1，该函数无量纲。

F(r，θ)为各向异性函数，用于描述角度θ对剂量分布的影响，其计算公式为：

(7)

显然，F(r，θ0)=1，且该函数无量纲。

综上可知，式(1)的实质就是先确定源中轴线上参考点处的剂量率，再通过几何函数做线源修正，最后利用径向剂量函数和各向异性函数建立待测点(r，θ)处的剂量率与参考点剂量率之问的关系。式(1)中需要确定的剂量计算参数有剂量率常数∧、径向剂量函数g(r)和各向异性函数F(r，θ)。

2 蒙特卡罗模拟计算

为保证125I-103Pd混合源的剂量学参数计算的准确性，可先利用TG-43报告中的6711型(3M)125I标准源进行剂量学参数计算，如计算值与报告中的结果一致，则说明计算方法正确。

2.1 6711型(3M) 125I源的计算

2.1.1源的几何描述及材料

6711型(3M)125I源整体为小圆柱形，125I均匀分布于内部圆柱形银棒的表面，其外包有1层钛包壳，两端为焊头。在圆柱状纯银棒上镀上厚度为2.0 μm含125I 的AgI和AgBr混合物。沿源长轴方向的剖面图示于图2，蒙特卡罗模拟软件为MCNP4C。

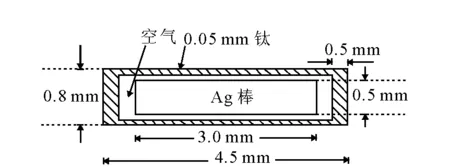
图2 6711型(3M) 125I源的内部结构Fig.2 Structure of 6711 type source for 125I

2.1.2剂量率常数计算

根据式(2)和式(3)，分为2步计算。

1) 空气比释动能强度计算

TG-43U1 报告中建议：计算空气比释动能强度时，源与空气比释动能记录体之间应该设置为真空。沿6711型125I粒子源中垂轴方向，设置一个内半径为100 cm、厚度为1.0 mm、高度为1 cm的指环状圆柱体。指环状圆柱体和粒子源之间的材料设置为真空，指环状圆柱体的材料为空气。计算指环状圆柱体中的空气比释放动能，把计算得到的空气比释动能与内半径的平方的乘积即是6711型125I粒子源的空气比释动能强度。

2)剂量率常数计算

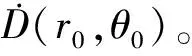
根据上面的剂量率常数计算方法，本次∧=0.862 cGyh-1·U-1。TG-43推荐的数值为0.88 cGyh-1·U-1。计算值与TG-43推荐值间的相对偏差为2%，符合较好。

2.2 混合源模型的计算

2.2.1源的几何描述及材料

混合源的几何模型与6711型(3M)125I源的内部结构相似，不同的是外层钛壳两侧为半球形，中间为C棒，混合源的核素由125I和103Pd组成，其混合比例假定为1 mCi125I和2 mCi103Pd。

图3 混合源结构Fig.3 Structure for hybrid source

2.2.2剂量率常数计算

对125I、103Pd、混合源三种源分布的空气比释动能强度和剂量率常数Λ(cGy·h-1·U-1)进行计算：

Sk=A·η·3 600×106·D空气

(8)

其中，A为活度，η为核素平均每次衰变发出的γ射线数，D空气为距离放射源1 m处的剂量，计算结果列于表1。

表1 三种源模型的空气比释动能强度和剂量率常数

2.2.3径向剂量函数g(r)

建立半径为30 cm的液态水球模型。球心放置种子源，在源中垂轴方向上布置1组计算点。分别距源中心0.5、1.0、2.0、3.0、4.0、5.0、6.0、7.0 cm。计算上述位置上的吸收剂量，依据式(6)求得各距离上的g(r)。计算获得的径向剂量函数g(r)列于表2。

出于实用目的，对表2中的混合源数据进行拟合，所得g(r)经验公式如下：g(r)=1.278 74-0.206 08r-0.098 57r2+0.041 56r3-0.005 73r4+2.751 78×10-4r5。

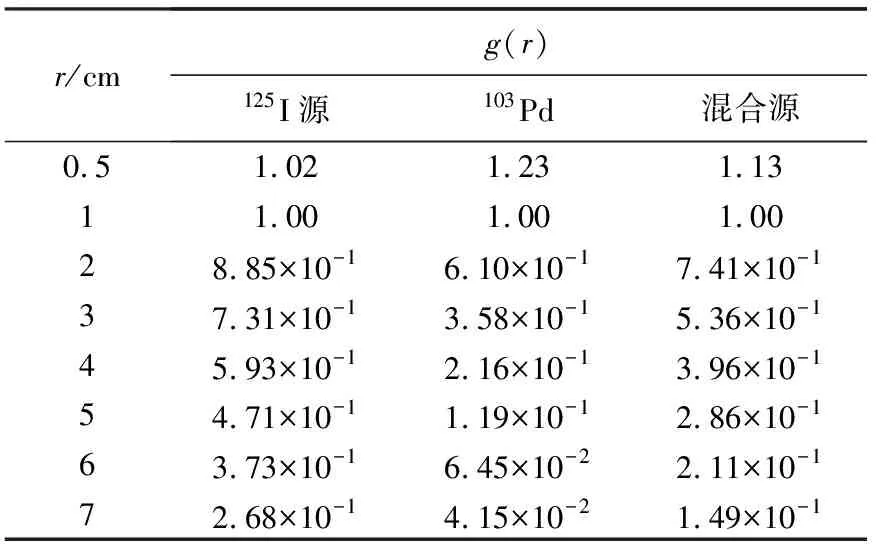
表2 混合源模型的径向剂量函数g(r)

2.2.4各向异性函数F(r，θ)

建立与2.2.3节中相同的液态水球，距离r取0.5、1.0、2.0、3.0、4.0、5.0、6.0、7.0 cm，因源结构左右对称，故角度θ取0°～90°，间隔5°。计算各位置处的吸收剂量，然后依据式(7)求得各向异性函数F(r,θ)，结果列于表3。结果表明：不同距离r随着极角θ的增加F(r,θ)随之增加，并在θ为90°时增加到1，与实际相符。

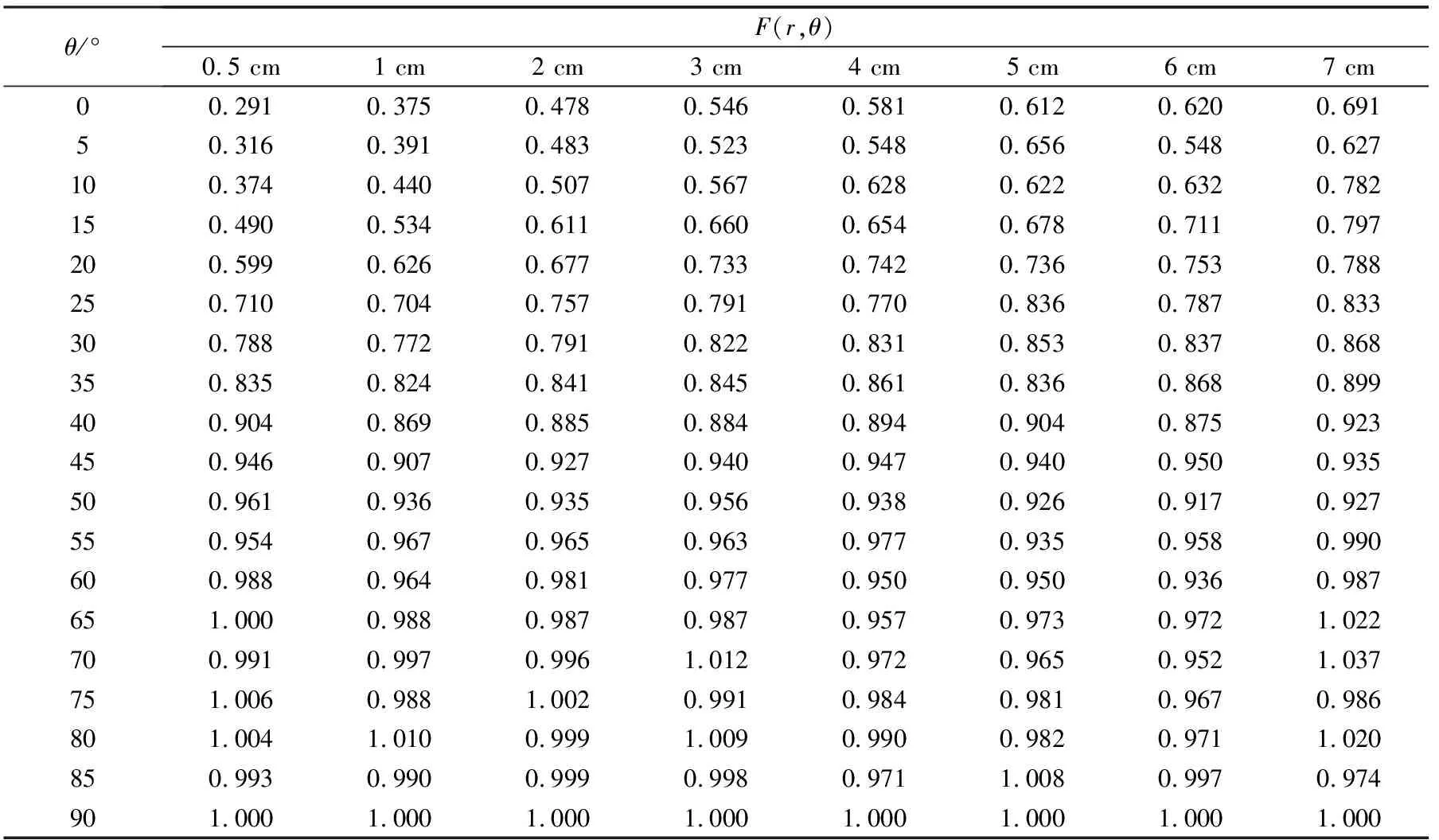
表3 混合源各向异性函数F(r,θ)

4 小结

根据AAPM TG-43U1 的关于植入治疗粒子源的剂量学参数的相关定义，首先在6711型125I粒子源尺寸基础上建立适用于MCNP4C的计算模型，利用MCNP4C 程序计算了6711型125I粒子源的剂量学参数。计算结果符合性较好，验证了计算方法的正确性。根据125I-103Pd混合源的实际参数建立了混合源计算模型，并给出相应的剂量学参数，如剂量率常数、径向剂量函数g(r)和各向异性函数F(r,θ)，对下一步混合源的研发工作提供参考。

参考文献：

[1]Rivard MJ, Coursey BM, DeWard LA, et al. Update of AAPM Task Group No.43 Report：A revised AAPM protocol for brachytherapy dose calculations[J]. Med Phys, 2004, 31：633-674．

[2]Wang JH, Liu W, Xu XJ, et al. Dosimetric parameters of palladium-103 brachytherapy source with Monte Carlo Simulation[J]. Chin Sci Bulletin, 2008, 53: 1 304-1 309．

[3]Rivard MJ. Comprehensive Monte Carlo calculations of AAPM Task Group Report No.43 dosimetry parameters for the Model 3500 I-Plant125I brachytherapy source[J]. Applied Radiation and Isotopes, 2002, 57: 381-389.

[4]Nath R, Anderson LL, Luxton G, et a1. Dosimetry of interstitial brachytherapy sources： recommendations of AAPM radiation therapy committee task group No.43[J]. Medical Physics, 1995, 22:209-234．

[5]孙亮，李君利.125I短程治疗源剂量计算参数的蒙特卡罗确定[J]. 原子能科学技术, 2006,40(6):657-661.

Sun Liang， Li Junli. Determination of Dose Calculation Parameters of125I Brachytherapy Source With Monte-Carlo Method[J]. Atomic Energy Science and Technology, 2006, 40(6): 657-661(in Chinese).

[6]花正东,王德忠.125I植入治疗源的剂量学参数的MonteCarlo模拟[J]. Intervent Radiol, 2010, 19(1): 38-41.

Hua Zhengdong, Wang Dezhong. Monte Carlo simulation of dosimetric parameters for the Model 6711125I brachytherapy source[J]. Intervent Radiol, 2010, 19(1): 38-41(in Chinese).