脉冲中子-裂变中子铀矿测井技术的蒙特卡罗模拟

王新光, 王国保, 张国光, 窦玉玲, 丰树强, 赵 潇

(中国原子能科学研究院 核技术应用研究所，北京 102413)

在铀矿勘探中，常用的自然γ能谱测井方法通过探测铀的衰变产物镭的γ放射性确定地层的含铀量，由于存在铀镭平衡系数确定困难的问题，在平衡系数不确定的地区需要从井下取岩心，才能相对准确的确定铀含量，耗费时间，增加了勘探成本。中子铀矿测井技术探测地层中的铀元素被中子激发产生的裂变中子，直接反映地层中铀含量，提高勘探效率，降低成本，优势明显。通过探测瞬发裂变中子确定地层含铀量的测井方法称为瞬发裂变中子铀矿测井；探测缓发裂变中子的称为缓发裂变中子铀矿测井。1962年，Amiel[2]在实验室条件下利用缓发中子定量确定裂变核的含量。Igumnovz[3]在1966年提出采用Po-Be源，利用探测缓发中子的方法探测铀矿。1972年，Czubek[4]通过实验数据提出一种探测瞬发中子的测井方法，并且通过理论推导说明探测缓发中子也是一种可行的方法，并且需要每秒109的中子源产额。Givens等[5]在1972年提出了利用能量为14 MeV的脉冲中子源进行缓发中子测井，并利用中子孔隙度资料对结果进行了校正。1982年，Barnard[6]提出利用超热中子和热中子平均寿命的计算模型，超热中子计数和热中子平均寿命的比值作为反应地层含铀量的测井响应。

本研究利用蒙特卡罗方法(MCNP)[7-10]分析了脉冲中子源产生快中子和铀产生裂变中子的时间规律，研究了裂变中子和地层含铀量的关系，并提出利用地层宏观俘获截面进行孔隙度校正的方法。

1 裂变中子铀矿测井原理[1]

235U为易裂变核，在不同的中子能量条件下具有不同的裂变反应截面，和快中子可以发生快裂变，和热中子可以发生热裂变，而且热裂变截面大于快裂变截面。238U需要一定的中子能量才能发生裂变反应，因此主要和快中子发生快裂变。裂变过程中放出的中子，统称为裂变中子。裂变中子99%以上都是在裂变的瞬间(约10-14S)释放出来，称为瞬发中子；不到1%的裂变中子是在裂变发生一段时间后，由某些裂变碎片经一系列的衰变过程放出的，称为缓发中子。

缓发中子铀矿测井通过记录快中子进入地层和地层中的238U和235U发生快裂变反应后，由裂变碎片产生的缓发中子；瞬发中子测井记录的是快中子进入地层被慢化后，热中子和235U发生热裂变产生的瞬发中子。由于产生缓发中子的衰变过程具有一定的半衰期，因此缓发中子测井在中子源脉冲结束后需要较长的等待时间，在源中子完全消失后，记录到的才是缓发中子；而热中子和235U发生热裂变产生的瞬发中子能量较高，平均能量为1.98 MeV，因此记录的是中子源脉冲结束后，超热中子能量范围的瞬发中子。缓发中子和瞬发中子测井记录的中子都是由地层中的铀发生裂变产生，因此理想条件下，在不含铀地层裂变中子测井计数为零，在周围地层环境不变的情况下，测井计数和地层含铀量有正比关系。在实际地层环境下，需要对中子分布有影响的地层因素进行环境校正。

2 蒙特卡罗数值模拟

2.1 计算模型

利用 MCNP程序建立裸眼井条件下的数值计算模型：井眼直径为14 cm，井眼中充满淡水，地层设内外半径分别为7 cm和70 cm，高为140 cm的圆筒状，地层骨架为含铀砂岩，主要成分为二氧化硅和铀，孔隙中饱含淡水。测井仪器采用14 MeV的D-T脉冲中子源，中子源与中子探测器之间的源距为30 cm，中子源和探测器之间利用理想屏蔽体进行屏蔽。采用栅元通量计数，模拟的快中子源粒子数为1×108个，采用分裂与赌的减小方差技巧，保证计数误差小于1%。仪器贴井壁测量，数值模拟的地层和仪器模型示意图示于图1。

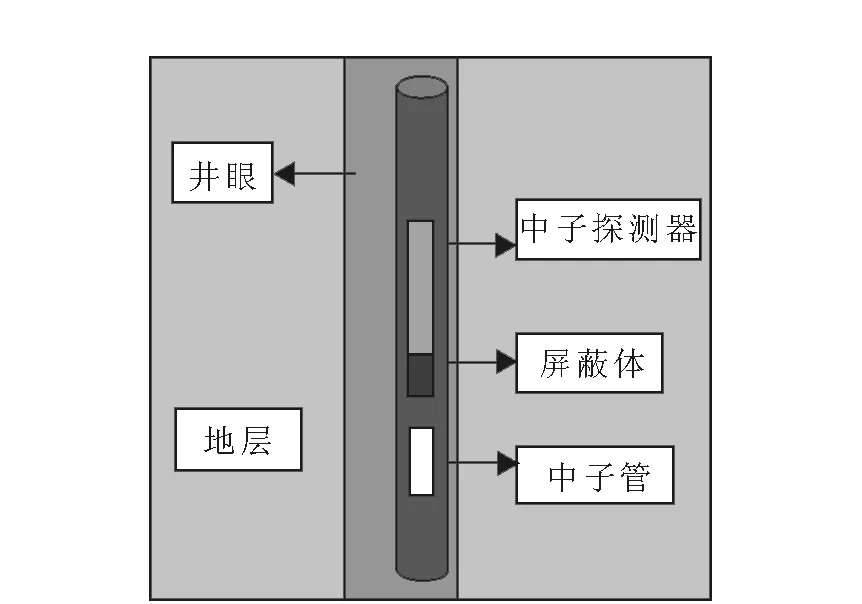
图1 蒙特卡罗模拟模型示意图

2.2 瞬发裂变中子铀矿测井模拟

瞬发裂变中子测井技术利用外表依次包裹慢化体和镉片的3He探测器，记录地层中由于发生瞬发裂变而增加的超热中子计数。中子源脉宽20 μs，改变地层中铀的含量分别为0、0.4%、1%，在探测器处分别记录0～3 500 μs超热中子时间谱和热中子衰减谱，结果示于图2和图3。

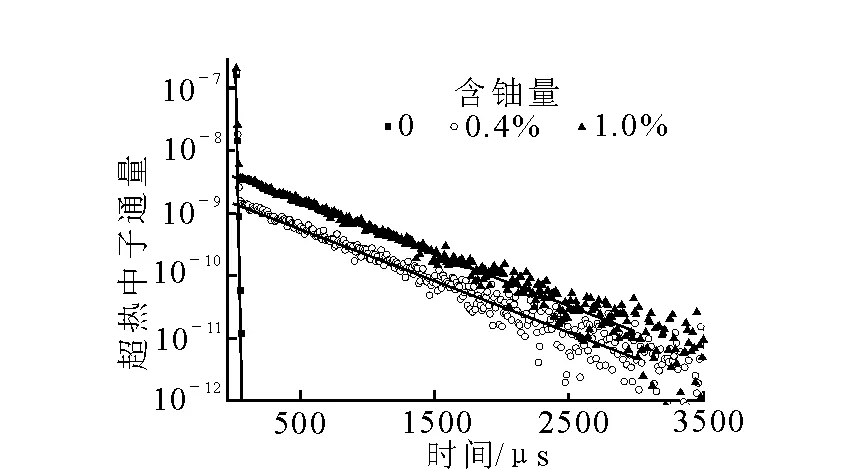
图2 不同铀含量地层超热中子时间衰减谱

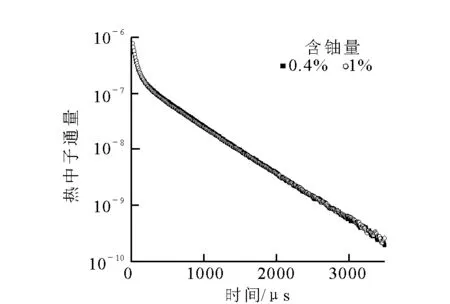
图3 不同铀含量地层热中子时间衰减谱

由图2和图3可以看出，地层铀含量对热中子时间谱影响不大，热中子时间分布按e-t/τ的规律衰减(τ为地层的热中子寿命)；超热中子受地层的含铀量影响较大，当地层中不含铀时，由源中子慢化产生的超热中子在t<100 μs的时间内完全消失；而当地层中含有铀时，超热中子通量明显增加，而且地层中含铀量越高，增加的超热中子越多，这主要是由于地层中含铀时，中子与铀发生裂变反应，产生的瞬发裂变中子增加了超热中子的通量。记录脉冲结束后一段时间内的超热中子通量计数，可以反映地层中铀的含量。而且由于超热中子通量的增加是由于热中子和235U发生热裂变产生的，因此含铀地层的超热中子通量衰减速度和热中子相同，即利用超热中子时间衰减谱可以计算地层的宏观吸收截面Σ。

2.3 缓发裂变中子铀矿测井模拟

缓发裂变中子测井利用3He探测器，记录源中子完全消失后由于发生裂变反应产生的缓发裂变中子计数。中子源脉宽40 μs，改变地层含铀量分别为0和0.5%，在探测器处分别记录单次脉冲产生的0～1 s热中子通量随时间的变化，结果示于图4。

由图4中可以看出，含铀地层和不含铀地层在源脉冲结束的初始热中子时间分布差别不大，但在t>5～8×103μs后，含铀地层仍然有热中子通量计数，而不含铀地层完全没有热中子通量计数。这主要是由于在含铀地层中，中子源产生的快中子和铀发生裂变反应，产生缓发裂变中子，增加了地层中的热中子通量。因此记录源中子完全被地层吸收后一定时间内的缓发中子通量计数，可以反映地层含铀量。

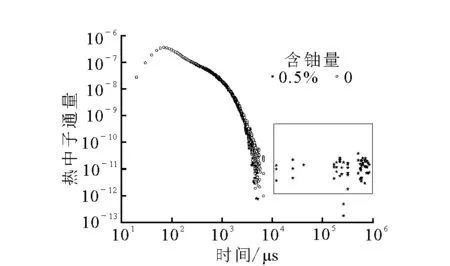
图4 不同铀含量地层热中子通量随时间变化

瞬发裂变中子测井和缓发裂变中子测井可以统称为裂变中子铀矿测井，探测的对象都是中子，易受到地层孔隙度和地层水矿化度的影响。利用瞬发裂变超热中子时间衰减速度和热中子相同的规律，对瞬发裂变中子测井和缓发裂变中子测井分别记录超热中子和热中子时间衰减谱，计算地层的中子宏观俘获截面，对计算结果进行校正。

2.4 地层孔隙度对裂变中子测井的影响及校正

地层孔隙度分别设为5%、10%、15%、20%、25%，含铀量分别设为0.2%、0.4%、0.6%、0.8%、1%，在探测器处记录源脉冲结束后0～2 000 μs的超热中子时间衰减谱和0～1 s的热中子时间衰减谱。利用超热中子时间衰减谱计算时间150 μs～2 000 μs的超热中子总计数及地层宏观俘获截面，利用热中子时间谱计算5 ms～1 s的热中子总计数和地层宏观俘获截面，从而得到不同铀含量地层的瞬发超热中子与地层孔隙度和含铀量的关系，结果示于图5和图6。

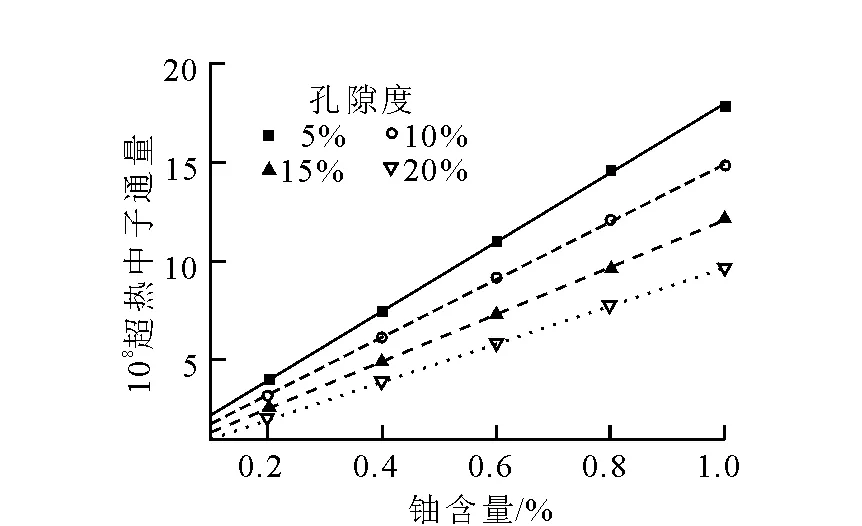
图5 瞬发超热中子通量与地层含铀量关系

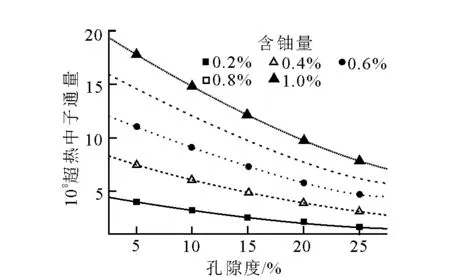
图6 瞬发超热中子通量与地层孔隙度关系

由图5和图6可以看出，在地层孔隙度条件一定时，瞬发超热中子通量和地层含铀量呈线性关系，随着地层含铀量的增加，瞬发超热中子通量增加；在地层含铀量一定时，瞬发超热中子通量和地层孔隙度呈反比关系，随地层孔隙度的增加，瞬发超热中子通量减少，而且超热中子对地层含铀量的分辨灵敏度随孔隙度的增加变差。

缓发中子与含铀量和地层孔隙度的关系和瞬发中子类似，结果示于图7和图8。在相同的地层孔隙度条件下，缓发中子通量随地层含铀量增加而增加；含铀量相同时，缓发中子通量随孔隙度的增加而减小。

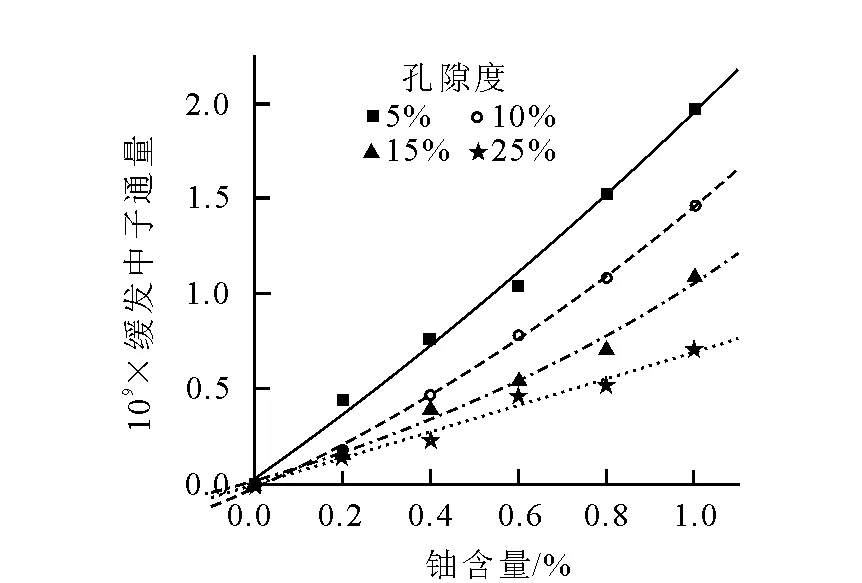
图7 缓发中子通量与地层含铀量关系

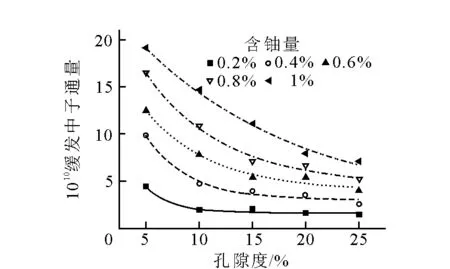
图8 缓发中子通量与地层孔隙度关系

孔隙度对瞬发中子和缓发中子都有较大的影响，孔隙度越大，利用裂变中子计算的地层含铀量越小。为计算得到准确的地层含铀量，需要进行孔隙度校正。孔隙度对裂变中子的影响，可以用地层的宏观俘获截面的变化表示。利用记录的超热中子和热中子时间衰减谱分别计算不同地层的宏观俘获截面，得到不同含铀地层的宏观俘获截面和地层孔隙度的关系，结果示于图9。

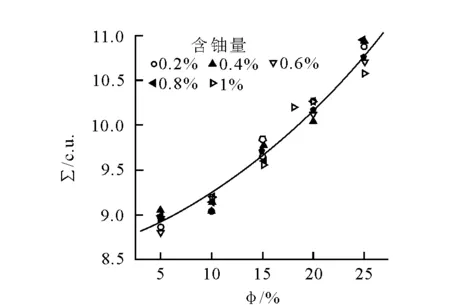
图9 地层宏观俘获截面与地层孔隙度、含铀量关系

由图9可以看出，地层含铀量对地层的宏观俘获截面影响不大，截面值主要受地层孔隙度影响，因此可以利用宏观俘获截面和孔隙度的关系，实现地层孔隙度对铀矿测井结果影响的校正。利用图6、图8、图9中数据可以得到利用宏观俘获截面值进行孔隙度校正的图版，结果示于图10和图11。

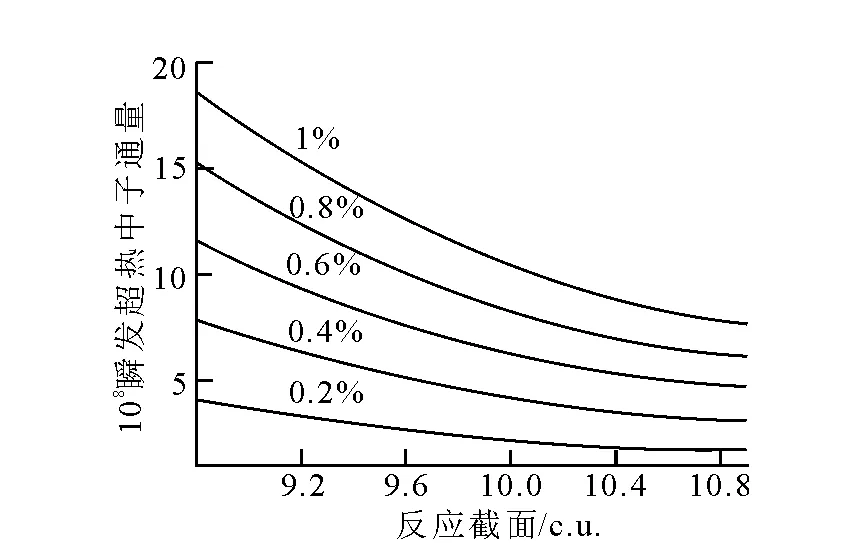
图10 瞬发超热中子通量的Σ校正图版

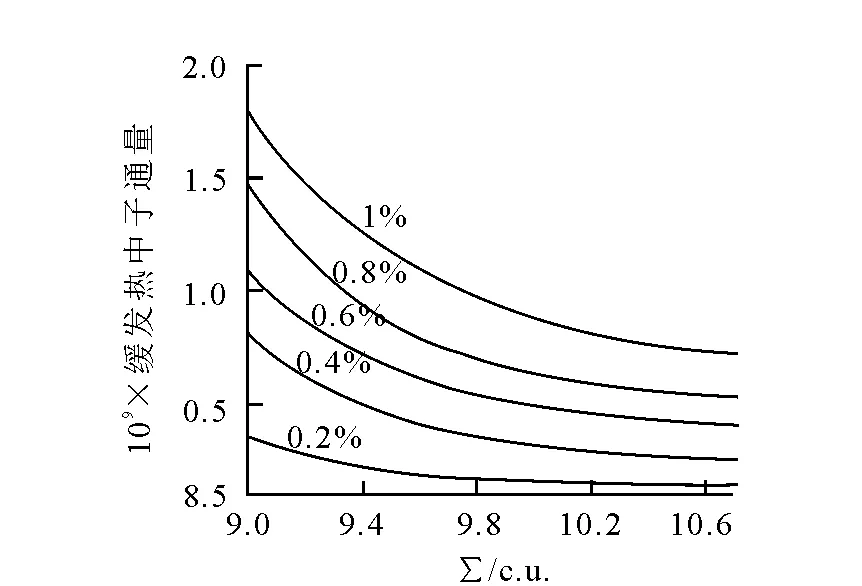
图11 缓发中子通量的Σ校正图版

根据图10、图11的校正图版，利用热中子时间衰减谱或瞬发裂变超热中子时间衰减谱计算得到地层的宏观俘获截面值，对测井得到的缓发热中子计数或瞬发超热中子计数进行校正，从而得到不受地层孔隙度影响的地层真实铀含量。

3 结 论

1) 脉冲中子源脉冲结束后超热中子能量范围的瞬发裂变中子和热中子能量范围的缓发裂变中子，和地层含铀量呈正比关系，裂变中子计数越多，地层含铀量越大。

2) 利用裂变中子计算地层含铀量受到地层孔隙度的影响，地层含铀量相同时，孔隙度越大，裂变中子计数越小。

3) 瞬发裂变超热中子和热中子衰减速度相同，可以利用瞬发裂变超热中子时间衰减谱计算地层的宏观俘获截面，且地层含铀量对宏观俘获截面影响不大，可以利用地层宏观俘获截面进行孔隙度校正，得到了利用地层宏观俘获截面进行校正的图版。

参考文献:

[1] Amiel S. Analytical applications of delayed neutron emission in fissionable elements[J]. Analyt Chem， 1962, 34: 1 684-1 692.

[2] Igumnov SA. On the utilization of delayed neutrons for direct uranium determination in bore-holes without coring Izv Vys Uchebn Zaved[J]. Gor-nyy Zhurn, 1966, 2: 3-6.

[3] Czubek JA. Pulsed Neutron Method for Uranium Well Logging[J]. Geophysics, 1972, 37(1): 160-173.

[4] Givens WW, Mills WR, Dennis CL, et al. Uranium Assay Logging Using a Pulsed 14Mev Neutron Source and Detection of Delayed Fission Neutrons[J]. Geophysics, 1976, 41(3): 468-490.

[5] Ralston WB, Jensen Dal H. Method of Assaying Uranium with Prompt Fission and Thermal Neutron Borehole Logging Adjusted by Borehole Physical Characteristics.United States Patent, 4350887 [P]. 1982-09-21.

[6] 张锋，靳秀云，侯爽. D-T脉冲中子发生器随钻中子孔隙度测井的蒙特卡罗模拟[J]. 同位素，2010，23(1)：15-21.

Zhang Feng, Jin Xiuyun, Hou Shuang. Monte Carlo Simulation on Compensated Neutron Porosity Logging in LWD With D-T Pulsed Neutron Generator[J]. Journal of isotopes, 2010, 23(1): 15-21(in Chinese).

[7] 张锋，黄隆基. 钆示踪中子伽马能谱测井方法的蒙特卡罗模拟[J]. 同位素，2007，20(4)：193-198.

Zhang Feng, Huang Longji. Monte Carlo Simulation of Gadolinium Neutron Gamma Spectroscopy Tracer Logging Method[J]. Journal of isotopes, 2007, 20(4): 193-198(in Chinese).

[8] 张锋，张高龙，贾文宝. 利用252Cf 源对镍精矿进行中子活化分析[J]. 同位素，2005，18(3)：129-133.

Zhang Feng, Zhang Gaolong, Jia Wenbao. Neutron Activation Analysis of Nickel Concentrates Samples With ～(252)Cf Neutron Source [J]. Journal of isotopes, 2005, 18(3 ): 129-129(in Chinese).

[9] 张锋，董经利，许玉俊，等. 脉冲中子全能谱测井数据处理方法及影响因素的模拟研究[J]. 同位素，2008，21(2)：70-77.

Zhang Feng, Dong Jingli, XuYujun. Monte Carlo Simulation for the Detector of C/O Ratio Spectroscopy Logging[J]. Journal of isotopes, 2008, 21(2): 70-77(in Chinese).

[10] 张法邦，吴清泉. 核反应堆运行物理[M]. 北京：原子能出版社， 2000.