基于Lingo后勤运输优化模型研究

　　摘要：本文结合数学建模和软件求解的方法，建立了平时情况下的后勤运输优化模型，并给出了模型的通用解法。通过对实例的分析和求解，说明了该模型的有效性和通用性。
　　关键字：后勤运输；优化；LINGO
　　后勤运输问题是伴随后勤保障问题而产生的，是资源在特定约束条件下的分配问题。本文拟通过数学建模的方法对平时后勤运输问题建立优化模型，以假设的一后勤运输问题为背景，通过建立数学模型和编写LINGO程序对这类问题进行求解。
　　一、问题背景
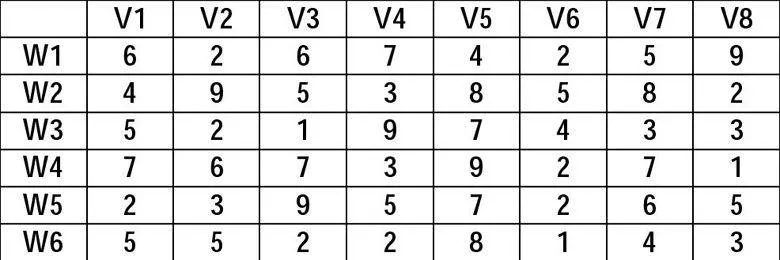
　　某后勤部门下属有6个物资仓库存储有某种通用物资，各仓库库存某物资数量分别为60，55，51，43，41，52箱，现有8个单位请领这一物资，数量分别为35，37，22，32，41，32，43，38。现联勤部门准备给8个缺少这批物资的单位发送所请领的物资，将其运至各场站附近车站等地，由请领单位派人领取运回。由于天气原因，需要在规定时间内完成对所有请领物资的发放。各仓库到各请领单位附近车站的单位物资运输耗费见下表：
　　仓库至车站单位物资耗费表
　　由上表，制定计划的参谋通过拼凑可找出一可行解，以下即为一可行解：即：W1、W2分别向V1运送19、16个单位的物资；W2向V2运送37个单位的物资；W3向V3运送22个单位的物资；W4向V4运送32个单位的物资；W1向V5运送41个单位的物资；W3、W6分别向V7运送23、20个单位的物资；W2、W4、W5分别向V8运送18、9、11个单位的物资。基于这一可行解的总费用为：
　　Z=6×19+4×16+37×9+22×1+32×3+41×4+32×1+23×3+20×4+9×1+18×2+11×5=1154
　　现在的问题在于这一可行解是不是最优解，怎样才能找到最优解，即花费最小完成任务。为此需要通过建立数学模型来进行求解。
　　二、问题假设
　　1、每个保障单位对物资的时间较充裕。2、单位里程的消耗是均匀的。
　　三、符号约定
　　xij：从第i个仓库到第j个车站的物资运量。cij：从第i个仓库到第j个车站的单位物资运输费用。
　　ai：从第i个仓库的物资储量。dj：从第j个场站的请领量。
　　四、模型建立
　　引入决策变量xij，代表从第i个仓库到第j个车站的物资运量，用cij表示从第i个仓库到第j个车站的单位物资运价，aij表示从第i个仓库的物资储量，dij表示从第j个场站的请领量。
　　五、模型求解
　　对于线性规划问题，一般使用LINGO软件求解，LINGO是专门用来求解各种规划问题软件包，其功能十分强大。是求解优化模型的最佳选择。以下为LINGO求解的过程。
　　1.集合定义部分。先定义仓库集合： CK/K1...K6/:ZL；其中CK是集合的名称，K1...K6是集合内的成员，“..”是特定的省略号，表明该集合有6个元素，对应六个仓库，ZL是集合的属性，表示仓库的物资总量。
　　同理，定义车站集合， CZ/Z1..Z2/:QL；为了表示数学模型中的运输关系以及与此相关的运输单价和运量，在定义一个表示运输关系的集合 LINKS(CK，CZ):C，X；该集合是以CK和CZ为基础产生的衍生集合（或称派生集合）。C，X为衍生集合的两个属性，分别表示到相应车站的单位货运价和从某仓库的到某车站的货运总量。
　　2.数据初始化。定义的集合中，X（有48个元素）是决策变量，是待求系数，属性ZL、QL和C的元素已知。数据初始化只需在程序中按语法输入即可。
　　3.目标函数和约束条件。目标函数表达式的LINGO程序为：MIN=@SUM(LINKS(I，J):C(I，J)*X(I，J))；式中， @SUM是求和函数，第一个参数LINKS(I，J），表示求和函数是对衍生集合进行；第二个参数为表达式C(I，J)*X(I，J)。
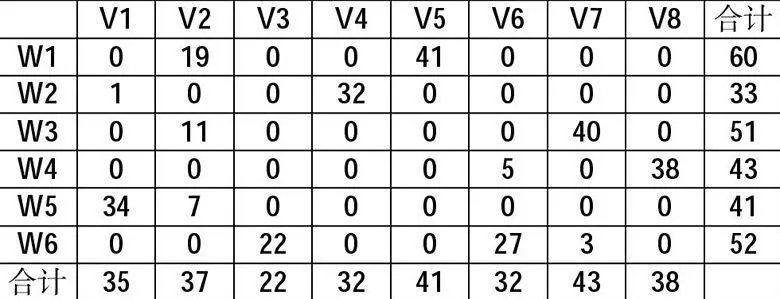
　　4.运算结果。通过编程计算，结果表明：目标函数值为664，即最省的方案下总费用为664.最优运输方案如下，该方案下完成任务花费的费用最省。
　　六、 结束语
　　后勤运输优化是一个大规模的线性规划问题，本文考虑到篇幅限制假设背景只是少数仓库对少数保障单位的情况，实际情况往往比这复杂的多。本文建立的数学模型和求解方法适用于后勤运输的大部分情况，在求解的过程中，只需改变初始的矩阵即可，具有较强的通用性，Lingo是解决规划问题专业软件，与其他大型的数学软件相比较，LINGO在线性规划，整数规划，0-1规划以及图论和网络模型的求解方面多具有很多的优势，可以考虑基于Lingo开发相关的后勤运输优化软件。将对后勤运输效能的提高具有一定的促进作用。
　　（作者单位：空军勤务学