感受数学思想方法的魅力

　　2001年颁布的《数学课程标准》（实验稿）第一次将“基本的数学思想方法”作为学生数学学习的目标之一，要求通过义务教育阶段的数学学习，学生能够“获得适应未来社会和进一步发展所必需的重要数学知识（包括数学事实、数学活动经验）以及基本的数学思想方法和必要的应用技能”。《数学课程标准》（2011版）则将上述课程目标进一步概括为“四基”，即数学的基础知识、基本技能、基本思想和基本活动经验。
　　可见，《数学课程标准》（2011版）已经不再局限于通过渗透数学思想方法加深对数学知识的理解，而是把感悟数学思想方法当做数学课程整体目标的一个有机组成部分，关注基础知识、基本技能、基本思想和基本活动经验这些显性和隐性目标的整体实现。这是一种全新的数学教育观，是对我国小学数学重视“双基”的继承和发展。
　　我们的数学课堂应该致力于追求数学思想的价值引领，充分挖掘教材中的数学思想，在教学中有意识地加以渗透和运用，启迪、发展学生的数学思维，激发学生的学习兴趣和学习主动性，促使学生形成牢固、完善的认识结构，让学生在潜移默化中去领悟、运用，并逐步内化为数学思维品质。
　　一、在教材中提取
　　第一，坚持教材分析的整体性。作为小学数学教师，我们应该深刻理解小学数学的知识体系，能够从数与代数、图形与几何、统计与概率、实践与综合应用四个方面，通晓小学数学的全部教学内容，逐步了解各部分渗透的数学思想方法，以便渗透时逐步推进，避免顾此失彼。斯苗儿老师曾经说过：“一些课上得不好的原因不在于方法和技巧，而是教师本身的数学功底。”因此，我们应该做到从整体上把握教材，认清教材特点，梳清教材脉络，理清教材思路，从整体上构建教材中数学思想的立体框架。
　　第二，坚持教材分析的独特性。教师应根据学生的认知规律和现有水平，领会教材的编写意图，同时也不应受教材的约束和限制，要学会灵活地处理教材，创造性地使用教材，实现数学思想有机融合在数学知识的形成过程中。在研读教材时，我们要多问自己几个为什么，如怎样才能唤起学生进行深层次的数学思考，如何引导学生主动探究新知，怎样根据教材的编排意图适时地渗透数学思想方法等。努力让数学课本上看得见的思维结果，折射出看不出的思维活动过程，弄清新知的形成过程，将教材的编排思想内化为自己的教学思想，找准新知教学的生长点。
　　如在一年级的教材中，经常会出现这样的习题：
　　6－□＞4 12＞4＋□ 6＋□＜10
　　7＜15－□ □＋8＜13 10＞5＋□
　　虽然这些题目只是要求学生在空格中填进一个合适的数，但我们应该明白，若把□换成x，则上面的题目就变成了不等式。这时x就是一个变元符号，就会有一定的取值范围，这一个“位置占有者”的作用就会凸显出来。我们可以引导学生思考、讨论一些这样的问题：□内最大能填几？最小呢？最多能填几个数？同样，在此基础上还可以进一步深化：□＋○＜7，可以填些什么数？这样的处理更好地渗透了符号变元这一数学思想，教材的思维价值才能显露出来。
　　二、在过程中渗透
　　数学思想往往呈隐蔽的形式，沉积、凝聚在数学结论的背后，常常渗透在学生获取知识和解决问题的过程中。著名数学家波利亚认为学习任何知识的最佳途径，都是由自己去发现、探究，因为这种理解最深刻，也最容易掌握其中的内在规律、性质和联系。我们应该有效地引导学生去经历知识形成的过程，让学生在观察、实验、分析、抽象、概括的过程中，体验到知识背后所负载的方法、蕴涵的思想。唯此，学生所掌握的知识才是鲜活的，这样的学习才是充满智慧的。我们应该引导学生在经历思想方法的过程中去感受和理解数学思想，促使学生对数学知识的理解达到领悟的水平。
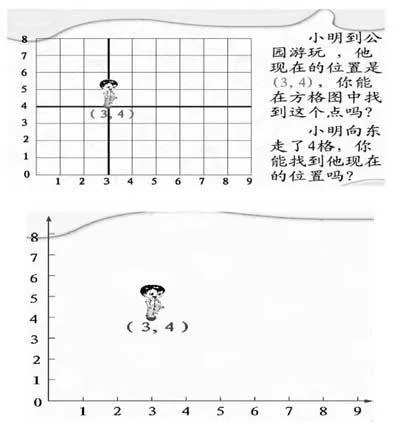
　　在《用数对确定位置》