自主创新能力对我国经济增长影响的实证分析

葛腾飞

（安徽工业大学工商学院，安徽马鞍山，243002）

自主创新能力对我国经济增长影响的实证分析

葛腾飞

（安徽工业大学工商学院，安徽马鞍山，243002）

采用因子分析法提取出一个衡量自主创新能力的综合指标；以传统的经济增长模型为基础，构建包含有技术进步因素的长期经济增长模型，并基于面板数据的回归模型实证分析自主创新能力对经济增长的影响及贡献程度。研究发现：自主创新能力对我国经济增长存在显著的正向影响，但目前我国自主创新能力整体水平还很低，与资本和劳动等投入要素相比，自主创新能力对经济增长影响最小；自主创新能力在各省份之间是有差异的，具体表现为东部领先、中部居中、西部落后，这在一定程度上能进一步解释自主创新能力的差异是地区经济发展不平衡的原因之一。

自主创新能力；经济增长；面板数据模型

2011年3月16日胡锦涛总书记在参观“十一五”重大科技成就展时指出，完成“十二五”时期经济社会发展的目标任务，在激烈的国际竞争中赢得发展的主动权，最根本的是靠科学技术，最关键的是大力提高自主创新能力。

我国作为发展中的经济大国，技术的自主创新在推动技术进步以及经济增长中的地位和作用日益重要，自主创新与经济增长的关系也引起了国内学术界的广泛关注。众多学者对两者之间的关系进行了研究，陈柳和刘志彪利用1987—2003年我国各个省份的面板数据验证发现，本土的技术创新能力对我国经济增长具有显著的正面作用和因果关系，创新能力在中西部地区经济增长中的作用比东部地区更强，并认为区域创新能力的差异在某种程度上可能是经济发展不平衡的原因［1］；陈柳对长三角地区的实证研究表明，本土创新能力与该地区的经济增长存在显著正相关的关系［2］；杨俊利用我国1996—2004年省际面板数据进行的实证研究也表明，本国技术的自主创新已对经济发展作出贡献［3］。戴魁早（2008）运用协整检验、误差修正模型和Granger因果检验等计量方法，对我国自主创新能力、技术吸收能力与经济增长之间的关系进行了实证研究。结果表明，三者之间存在长期稳定的均衡关系，自主创新能力和技术吸收能力分别是经济增长的Granger原因；从长期看，两者对我国的经济增长都具有促进作用，且自主创新能力对经济增长的影响比较明显［4］。卢宁等基于区域自主创新系统视角，通过因素分析法提取八个区域自主创新主成分进行统计分析并建立面板数据模型［5］。齐晓丽等利用1998—2007年31个省市的面板数据分析了以专利申请受理量表示的自主创新与经济增长总量的关系及其在东中西部间的区域差异。结果显示经济发展水平越高要求自主创新的产出能力也越高,但是自主创新产出能力对经济增长的作用在各地区间存在着显著的差异［6］。

现有研究文献的着眼点主要在于研究自主创新能力和经济增长之间的相互关系，强调计量方法的运用和实证分析，模型缺乏必要的经济理论基础。并且在自主创新能力的衡量指标选取上方法众多，没有一个统一的标准。基于此，首先借鉴国际和国内常用的评价指标，并结合我国国情及数据的可得性，通过因子分析法提取出一个衡量自主创新能力得分的综合指标；其次，以传统的经济增长理论模型为基础，构建包含有技术进步因素的长期经济增长模型；再次，通过基于省际面板数据模型实证分析自主创新能力对经济增长的影响；最后，得到有关结论和对策建议。

一、自主创新能力评价

（一）指标选取

评价一个国家或地区创新能力的指标众多，借鉴国际和国内常用的评价指标，结合我国国情及数据的可得性，在此选取R&D经费投入、科研活动人员数、发明专利授权量、技术市场合同成交额等作为衡量我国自主创新能力的核心指标［7］。

1.R&D经费投入。R&D经费投入是自主创新的前提，为自主创新的顺利进行提供了物质保证，同时，R&D经费投入作为自主创新物质资源投入的重要指标，也是衡量一个国家或地区科技创新水平和实力的一个重要参数。

2.科研活动人员数。根据堪培拉手册和欧盟统计机构定义，科技人力资源指从本科及以上教育机构毕业的人或者是科技工作者。在此结合我国实际，主要选取R&D科研人员。选取该指标主要是因为科技人力资源是知识经济的重要支柱，也是一个国家创新能力建设的主力军。创新活动的主体是人，而科研工作者更易于萌发创新意识，从事创新活动。所以，科研人员数是衡量一个国家自主创新能力人力资源投入的又一重要方面。

3.发明专利授权量。我国专利法第二十二条规定：授予专利权的发明和实用新型，应当具备新颖性、创造性和实用性。各项发明专利只有满足新颖、创造、实用才能予以授权。专利有分发明、实用新型、外观设计三类。选取发明专利，主要考虑因素是发明专利相对其他两项在价值呈现方面更容易量化，更能体现自主创新能力的产出效应。

4.技术市场合同成交金额。技术市场合同成交金额反映的是当前该地区的自主创新能力在技术市场的货币表现，能有效衡量自主创新能力的产出效应，是衡量自主创新技术实现能力的重要指标。

（二）评价方法

基于上述对于自主创新能力的影响因素分析，在此采用因子分析法对自主创新能力进行综合评价，即通过因子分析法提取出一个主成分因子来拟合上述四个指标，记为自主创新能力得分。

（三）数据来源

数据来源于《新中国60年资料汇编》及相关年份《中国科技统计年鉴》和《中国统计年鉴》，时间跨度为2001—2009年。需要说明的是，由于缺乏西藏自治区部分年份的样本数据，遂选取我国除西藏外的30个省市的科研人员、R&D经费、发明专利授权量和技术市场合同成交金额4个变量作为自主创新能力的衡量指标。

（四）评价结果

在收集2001—2009年间各省的科研人员、R&D经费、发明专利授权量和技术市场合同成交金额数据后，先将各指标值进行标准化，再基于主成分方法进行因子分析，所使用的统计软件为SPSS17.0。结果如表1：

表1 KMO检验和Bartlett球形检验结果表

表1是KMO检验和Bartlett球形检验结果表。KMO检验用于检验变量间的偏相关系数是否过小。一般情况下，当KMO大于0.9时效果最佳，大于0.7小于0.8说明适合作因子分析，小于0.5时说明不适合做因子分析。Bartlett球形检验用于检验相关系数矩阵是否是单位阵，如果检验结论不能拒绝原假设，则表示各个变量都是各自独立的。从表1可以看出KMO检验结果0.731，大于0.7小于0.8；同时，Bartlett球形检验的Sig.取值是0，表示拒绝原假设，即相关系数矩阵不是单位阵，说明各个变量之间存在相关性，进行因子分析是合适的。

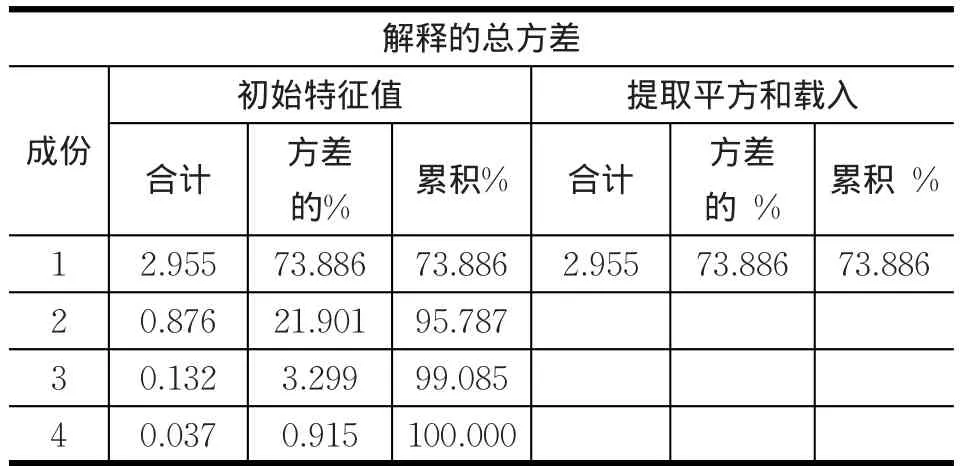
表2 各主成分解释原始变量总方差的情况

表2是主成分表，表中列出了所有的主成分，且按照特征根的从大到小次序排列。从表中可见，第一主成分的特征根为2.955，方差贡献率为73.886%，第二个主成分的特征根为0.876，方差贡献率为21.901%，前两个主成分的累计贡献率为95.787%。根据提取因子的条件——特征值大于1，本文只抽取了一个主成分因子，且该主成分因子集中了原始4个变量信息的73.886%，说明因子分析得到的主成分因子能代表4个变量的主要信息。

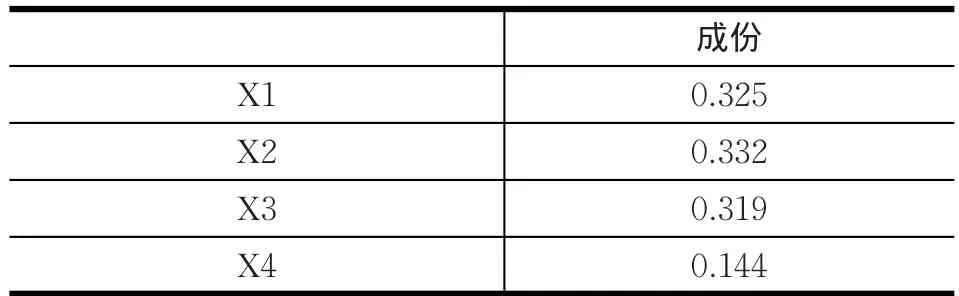
表3 因子得分系数矩阵

表3是因子得分系数矩阵，通过此表就可以得到以各个变量的线性组合表达的主成分，其具体的表达式为：

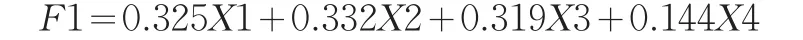
表中数据均已标准化，其中X1表示科技人员；X2表示R&D经费；X3表示发明专利授权量；X4表示技术市场合同成交金额；F1表示因子得分。通过上述方程可以计算出各省各年具体的自主创新能力得分。

为了进一步分析自主创新能力的地区差异情况，在此采用聚类分析法将我国各省市按自主创新能力得分值划分成5类，如表4：

表4 2001年和2009年30个省市自主创新能力得分的聚类分布

从表4的结果我们可以看到：与2001年相比，2009年北京的自主创新能力得分一直处在第一类；而广东的自主创新能力得分在此期间有所上升，由第二类晋升为第一类。上海、江苏一直保持在第二类水平，变化不大。 辽宁、山东、四川、湖北、浙江五个省份的自主创新得分排名也一直处在第三类水平。其余中、西部大多数省份表现出来的情况都是自主创新得分普遍不高，且2001年和2009年排名几乎都保持不变，都处在第四或第五类。值得注意的是，在这些省市中，除海南外，均为西部地区的省份。总的来说，从自主创新得分上的差异分布可以看出，各个省份的自主创新能力和各地区的经济发展水平一样都呈现出东部领先、中部居中、西部落后的情况。

二、自主创新能力对我国经济增长影响的实证分析

（一）模型构建

遵循着索洛（1965）开创的总量分析方法及其后的内生经济增长理论关于技术进步对经济增长贡献的研究路径，其基本分析思路大都采用柯布—道格拉斯总量生产函数的回归分析方法。柯布—道格拉斯生产函数的基本形式是：

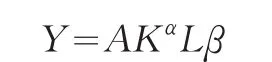
为了消除时间序列数据异方差性，对各变量进行自然对数变换，并且在模型中引入自主创新得分作为技术进步的因素，得到新的增长方程：

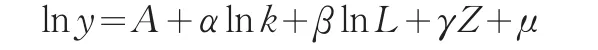
其中Y是经济发展水平，K是资本的投入数量，K是劳动力的投入数量；α是资本要素的产出弹性系数值，β为劳动要素的边际产出弹性系数值，Z为引入的技术进步要素，γ是技术要素的产出弹性系数，表示自主创新能力对于经济增长的影响水平，即衡量自主创新水平每增加一个单位对经济增长速度的贡献程度。

表5 模型回归分析结果

（二）变量选取

本文采用人均国内生产总值作为衡量经济发展水平的指标，采用固定资产投资额、就业人数和自主创新能力得分分别作为衡量资本、劳动力和技术等投入要素的指标。

（三）数据来源

数据来源于《新中国60年资料汇编》及2002—2010年《中国科技统计年鉴》和《中国统计年鉴》，包括除西藏外的30个省市自治区直辖市。时间跨度为2001-2009年。

（四）结果分析

本文采用固定效应的变截距模型对上述模型进行参数估计，使用的计量软件为Eviews6.0，估计结果如表5：

根据表5得到以下样本回归方程：

从上述回归分析结果可以看到：决定系数R2=0.9840，说明人均国内生产总值的总变异中有98.40%的部分可以由固定资产投资额、就业人数和自主创新得分等解释变量来联合解释，说明方程拟合得很好。又由F=506.2506，其对应的概率为0，小于显著性水平0.05，拒绝原假设，说明各解释变量与被解释变量人均国内生产总值之间线性关系显著，即方程总体是显著线性的。最后由上述回归方程括号内的t统计量以及其相应的概率值判断，其概率值都小于0.05，均拒绝原假设，说明每个解释变量对被解释变量都有着显著的正向影响。

此模型进一步说明：

第一，在国民经济中固定资产投资额（K）和就业人数（L）不变的前提下，自主创新得分（z）每增加1个单位，人均国内生产总值（Y）增加0.0342个单位，且自主创新能力对经济发展的影响是正向且显著的。

第二，当固定资产投资额（K）和自主创新得分（z）不变的情况下，就业人数（L）每增加一个百分比，人均国内生产总值增加0.3385个百分比。

第三，当就业人数（L）和自主创新得分（z）不变的情况下，固定资产投资额（K）每增加一单位，人均国内生产总值增加0.6264个百分比。

第四，由于采用的是固定效应变截距模型，各省区的生产函数模型估计结果是不一样的。具体来说，除了截距项外，各解释变量对被解释变量的影响方向和大小均是是一致的。

三、结论及建议

在此利用2000—2009年省际面板数据对我国自主创新能力与经济增长之间的关系进行实证分析，至少可以得到以下结论和建议：

第一，回归分析结果表明，资本投入、劳动投入和自主创新能力都对我国经济增长存在显著的正向影响，但影响程度各不相同。资本投入对经济增长影响最大，劳动投入次之，自主创新能力最小。说明目前我国自主创新能力整体水平还很低，对经济增长贡献不大，经济增长主要还是依靠传统的资本密集型和劳动密集型发展模式，这种粗放型的增长方式亟待转变。

第二，从自主创新得分的地区差异分布可以看出，各个省份的自主创新能力是有差距的，具体表现为东部领先、中部居中、西部落后的情况。这在一定程度上能进一步解释自主创新能力的差异是地区经济发展不平衡的原因之一。

第三，区域经济平衡发展是国家经济稳定健康发展的基础。因此，针对我国区域间自主创新能力发展不均衡的现实，建议政府要尽量平衡区域间在自主创新资源投入上的差距，加大对于欠发达地区自主创新能力的资源投入的力度，同时鼓励和引导欠发达地区对于自主创新能力的培养和投入。

［1］ 陈柳，刘志彪.本土创新能力、FDI技术外溢与经济增长［J］.南开经济研究，2006（3）：90-101.

［2］ 陈柳.长三角地区的技术外溢、本土创新能力与经济增长［J］.世界经济研究，2007（1）：60-67.

［3］ 杨俊.技术模仿、人力资本积累与自主创新：基于中国省际面板数据的实证分析［J］.财经研究，2007（5）：18-28.

［4］ 戴魁早.中国自主创新与经济增长关系的实证研究——基于技术吸收能力的视角［J］.科学学研究，2008（3）：626-632.

［5］ 卢宁，李国平，刘光领.中国自主创新与区域经济增长——基于1998—2007年省际面板数据的实证研究［J］.数量经济技术经济研究，2010（1）：626-632.

［6］ 齐晓丽，金浩.自主创新与经济增长总量的关系及其区域差异分析［J］.现代财经：天津财经大学学报，2010（6）：76-80.

［7］ 江苏省统计局.江苏自主创新能力与经济增长：相关性与比较研究［EB/OL］.（2011-02-04）.http://www.jssb.gov.cn.

F2

A

葛腾飞（1984-），男，硕士，助教，研究方向为宏观经济计量分析、资本市场统计分析。