男子百米成绩预测的数学模型

金庆红，黄贝君

（1.安徽工程大学体育学院，安徽 芜湖 241000；2.广州体育学院研究生部，广州 510500）

男子百米成绩预测的数学模型

金庆红1，黄贝君2

（1.安徽工程大学体育学院，安徽 芜湖 241000；2.广州体育学院研究生部，广州 510500）

先前有许多对田径比赛成绩进行预测的研究，使用的数学模型在不断优化.总体而言，非线性模型对于未来成绩的预测更为精确.本研究对2011年男子100 m成绩的预测结果显示，Cubic函数拟合效果最好（R2=0.787，P<0.01），误差仅为0.29%.因此，采用Cubic函数模型（R2=0.826，P<0.01）对2012年男子百米成绩进行预测.对比赛成绩进行预测的唯一意义在于检验预测的精确度.

男子百米；成绩预测；数学模型

对男子100 m成绩的预测是个常见的话题，问题的关键在于选择合适的数学模型以提高预测的精确度.以往，大多数预测不依赖于充实的证据，而是基于纪录被不断刷新的趋势[1].各个项目的数据来源于奥运会、世界纪录与世界最好成绩，通过数学模型的构建可以预测未来成绩的变化趋势.

基于先前比赛成绩，构建数学模型，用于未来田径比赛成绩预测的研究众多.Prendergast[2]较早提出人类速度是否有极限的问题.Péronnet等[3]认为男子100 m的极限为9 sec.Seiler[4]分析了过去50年世界纪录的变化，发现短跑项目的成绩每10年提高约1%，并指出男子100 m的速度没有极限.Heazlewood等[5]甚至预测了0至5038年间男子100 m的成绩变化，但结果自相矛盾，在随后的研究中[1]，亦显示其预测模型的不准确性.

本文应用曲线拟合的方法，试图寻找最佳的预测数学模型，并对2012年伦敦奥运会男子100 m的比赛成绩作出预测.

1 研究对象与方法

1999-2011年，男子100 m运动员年度最好成绩前10名数据来源于国际田联(International Association of Athletics Federations, IAAF)官方网站[6].其中，2001年数据未收集到.以往的研究多集中于对世界纪录的预测[7-9]，且多针对于奥运会或世锦赛.但是，世界纪录远不能代表一个项目的整体实力，且时间跨度较大.因此，本研究采用年度前10名最好成绩的平均值.

风速是影响100 m比赛成绩的重要变量，但大多数研究[1,5]并没有考虑到这一因素.Linthorne[10]研究指出，对于男子100 m项目来说，顺风2.0 m/s将促使比赛成绩提高0.10±0.01 sec.本文借鉴此标准对比赛成绩进行风速校正，见表1.

表1 1999-2011年度最好成绩前10名平均值

使用SPSS17.0(Chicago, IL, USA, 2008)对时间与修正成绩进行曲线拟合，在Matlab 6.5 (MathWorks,USA, 2002)平台上绘制有关图形.显著性水平为P<0.05，非常显著性水平为P<0.01.

2 结果与分析

表2 2011年成绩预测的拟合曲线参数

在对2012年的比赛成绩进行预测前，首先对1999-2010年的数据进行曲线拟合，寻找到合适的数学模型，并预测2011年的比赛成绩，以此对其精确度进行评估.曲线拟合的基本思想是通过构造一个逼近函数来表达样本数据的总体趋势和特征.其中，R2代表模型的精确度，R值越大，模型预测与实际情况的拟合效果越佳.

2011年比赛成绩预测的拟合曲线参数显示，Cubic函数的拟合效果最佳，R2=0.787，P<0.01.而Heazlewood[1]的研究显示，Linear函数对男子100 m成绩的拟合效果最佳，但其R2值仅为0.659.笔者认为这与其选取时间的跨度较大有关.使用Cubic函数对2011年的比赛成绩进行预测，结果显示其年度最好成绩前10名的平均值为9.856 sec，与其实际值9.884 sec相比，相差0.029 sec，误差为0.29%，精确度较高.

对1999-2011年的数据进行曲线拟合以此预测2012年的比赛成绩，亦发现Cubic函数的拟合效果最佳，R2=0.826，P<0.01，见表3.使用Cubic函数对2012年比赛成绩进行预测，得出其年度最好成绩前10名的平均值为9.868 sec（图1）.考虑到使用Cubic函数来预测成绩会呈现成绩逐渐提高的趋势，故对其预测成绩给予差值(0.029 sec)补偿，得出2012年度最好成绩前10名的平均值为9.897 sec.

表3 2012年成绩预测的拟合曲线参数

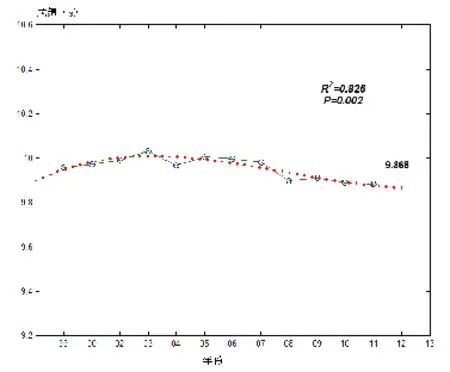
图1 2012年世界最好成绩前10名平均值预测

与此同时，对近3届奥运会男子100 m决赛前6名（考虑运动员伤病、犯规等意外情况）的成绩进行整理，结果显示其平均值为9.9467 sec，而奥运年年度世界最好成绩前10名的平均值为9.9463 sec，相差无几.本文根据这一结果对2012年伦敦奥运会男子100 m决赛前6名成绩的平均值进行预测（表5）.

表4 奥运会成绩与年度世界最好成绩的差值统计(sec)

表5 伦敦奥运会前6名平均成绩预测

基于先前的比赛数据可以对未来的比赛成绩作出预测，使用的数学模型多种多样.总体而言，非线性模型对比赛成绩的预测更为精确.大多数研究结果显示，预测成绩往往比实际表现要好得多，误差较大.事实上，男子100 m的成绩也在不断地提高，人们对于速度极限的认识也在不断调整.成绩的不断演变得益于合理的技术、科学的选材、庞大的基因库、生理机能的进化等因素.

虽然可以通过构建数学模型对比赛成绩的变化趋势作出预测，但实际成绩的取得是众多因素的综合反映.因此，提高对男子100 m成绩的预测精度并不是一件简单的事情，数学模型的预测仅仅反映了未来的变化趋势.对于比赛成绩的预测研究，最本质的目的是要发现成绩改进的限制因素，如生物力学、运动生理、技能学习与心理功能等，甚至是更复杂的趋势，如人类进化与运动适应等[1].

3 结论

构建比赛成绩预测的数学模型是一种启发式的练习，这类问题的唯一意义在于：让时间的流逝来检验我们预测的精确度.

[1] Heazlewood T.Prediction versus reality: the use of mathematical models to predict elite preformance in swimming and athletics at the olympic games[J].J Sports Sci Med, 2006, (5): 451-457.

[2] Prendergast K.What do world running records tell us?[J].Modern Athlete Coach, 1990, 28: 33-36.

[3] Péronnet F, Thibault G.Mathematical analysis of running performance and world running records[J].J Appl Physiol, 1989,67(1): 453-465.

[4] Hopkins W G.Limits to performance[EB/OL].http://www.sportsci.org/jour/0002/inbrief.html#limits, 2011-10-01.

[5] Heazlewood T, Lackey G.The use of mathematical models to predict elite athletic performance at the Olympic Games[C].Third Conference on Mathematics and Computers in Sport, Bond University,Queensland, 1996: 185-206.

[6] IAAF.Top lists [EB/OL].http://www.iaaf.org/statistics/toplists/index.html, 2011-10-01.

[7] Jokl E, Jokl P.Running and swimming world records[J].Br J Sports Med, 1976, 10(4): 203-208.

[8] Jokl E, Jokl P.Running and swimming world records[J].J Sports Med Phys Fit,1977,17: 213 - 229.

[9] Edwards D, Hopkins W.Targets for the future[J].Modern Athlete Coach,1979,17(3):34-36.

[10] Linthorne N P.The effect of wind on 100-m sprint times[J].J Appl Biomech,1994,10(2):110-131.

Mathematical Models to Predict Performance on Male 100 m

JIN Qing-hong1,HUANG Bei-jun2
(1.Sports College of Anhui Polytechnic University, Wuhu 241000,China;2.Institute of Guangzhou Sports University, Guangzhou 510500,China)

There were many previous researches to predict athletic performance, and the mathematical models used were in continuous optimization.Overall, non-linear model for future predict ions was more accurately.The results of predicted performance of men’s 100 m in 2011 indicated that Cubic functions fitted best (R2=0.787, P＜0.01), and the error was only 0.29%.Therefore, used Cubic function model (R2=0.826, P＜0.01)to predict performance on men’s 100 m in 2012.The only purpose of performance prediction was to test th e accuracy of performance prediction.

male 100 m; performance predicted; mathematical models

G822.1

A

1008-9128（2012）02-0095-03

2011-10-05

金庆红（1977—），男，安徽芜湖人，讲师，硕士.研究方向：体育教育训练、体育表演.

[责任编辑 姜仁达]