基于BRDF的粗糙目标表面统计建模与验证
曾建华,朱云东,方玉萍,刘 微,段剑金,李泽东,李宏宁,杨卫平
(云南师范大学物理与电子信息学院,昆明 650092)
基于BRDF的粗糙目标表面统计建模与验证
曾建华,朱云东,方玉萍,刘 微,段剑金,李泽东,李宏宁,杨卫平
(云南师范大学物理与电子信息学院,昆明 650092)
利用从五参量模型简化而来的BRDF模型对水泥板、花岗岩的实验数据进行优化拟合.通过与实测数据比较,结果表明,二参量模型对粗糙度大的目标表面BRDF统计建模是完全可行、有效的,但对粗糙度小的目标表面不适用.而三参量、四参量模型对各种样片表面都能得到较好的拟合效果.简化模型的准确性为粗糙目标表面统计建模简化了计算、节约了时间,便于进一步对粗糙目标作相关的多光谱成像研究与仿真.
双向反射分布函数BRDF;粗糙目标表面;简化模型
引言
1970年Nicodemus正式提出双向反射分布函数BRDF的定义[1],它既能描述粗糙表面的光辐射特性,也能描述方向散射特性,目前广泛应用于各种领域,例如目标光辐射和散射特性[2]、材料诊断、图像处理[3]等.粗糙目标样片BRDF可以通过实验测量[4][5]与理论计算[6]的方法来进行研究.但理论计算比较复杂,而且材料粗糙度参数也难以获取,所以在工程应用中往往采用根据材料的实验测量数据建立BRDF模型的方法.
文章将利用从五参量模型简化而来的BRDF模型对水泥板、花岗岩的实验数据进行优化拟合,通过比较拟合结果与实测数据,结果表明,三种简化模型对粗糙度大的目标表面BRDF进行统计建模都是可行、有效的,而具有方向性的样片表面只能采用三参量和四参量模型.
1 双向反射分布函数(BRDF)
1.1 双向反射分布函数(BRDF)概念
BRDF定义为表面散射指定方向的辐亮度与入射辐照度之比,如图1所示[7].它描述了物体在半球空间范围内的反射特性,其数学表达式为:

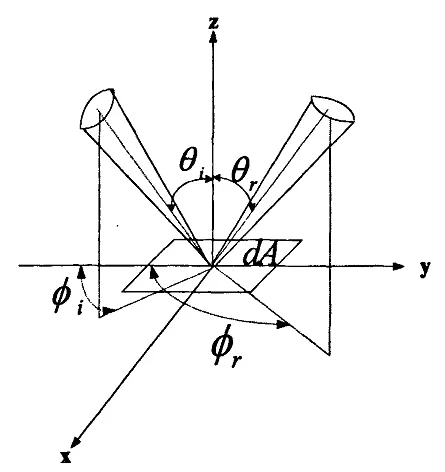
图1 BRDF方位角示意图
式(1)中 θi, ϕi为入射角和入射方位角,θr, ϕr则为反射角和反射方位角,d Lr( θi, ϕi; θr, ϕr) 是(θr, ϕr)方向的反射亮度,d Ei(θi, ϕi) 是(θi, ϕ)i方向的入射照度.
1.2 BRDF的测量
BRDF的测量有定义测量法、比较测量法及单一参考测量法[8],文章的BRDF数据采用比较测量法[4].聚四氟乙烯粉压制的标准白板最接近朗伯体[9],所以可以把它作为标准参考板,其双向反射分布函数为ρ0/π 。 ρ0可以通过计量定标或者用分光光度计加积分球测量获得.实验测试系统中的光电倍增管是一种能将光信号转换成具有一定电平的电信号的光电转换器件,所以测量目标表面的BRDF可以通过电压的测量得出.在相同的入射和接受条件下,参考板的输出电压为Vr(θi, ϕi; θr, ϕr),样品的输出电压为 Vs(θi, ϕi; θr, ϕr) ,则目标样品的BRDF为:
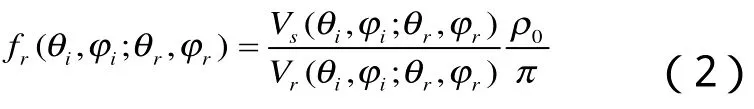
因标准白板是朗伯面板,所以只需测量参考板一个特定的散射角的散射信号电压,其散射特性满足:
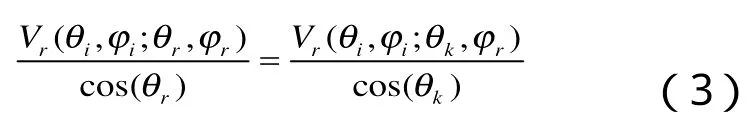
式(3)中θk表示某个特定的散射方向,表示参考板在θk散射方向的输出电压;θr表示任意散射角表示参考板在θr散射方向的输出电压.为提高效率,只需测量一个散射方向如θk=30°情况下的标准板的输出电压即可.把(3)式代入(2)式得[10]:

通过实验可以由(4)式得出样品在各种测量条件下的BRDF值,很多实验采用的就是比较测量法.
1.3 五参量BRDF模型的简化
在长期的研究中,很多BRDF模型已经形成,如Cook-Torrance模型、Phong模型、Wolf模型和五参量模型等[11],而有的模型复杂,计算也很耗时,所以有必要对数学模型合理简化.文章采用从五参量模型简化得到的三种模型,并采用一组实验数据[15-16]对粗糙目标表面BRDF进行拟合,以及对三种简化模型的拟合结果进行了分析比较.

如果把样片的镜向反射近似为0,则五参量模型可简化为二参量模型:

其中,a,k为待定参数.
如果用一个指数函数表示单次反射分量,另一部分为多次反射分量,则五参量模型可简化为三参量模型:

当表面具有一定的方向性时,利用一个指数函数与漫反射函数的组合五参量模型简化得到一个四参量模型:

其中a,b,c,d为待定参数.
2 拟合程度的评价[12]
所谓拟合程度,是指样本观测值集中在样本回归线周围的紧密程度.
用于判断回归模型拟合程度优劣最常用的数量指标是可决系数(又称为决定系数).
可决系数是建立在对总离差平方和进行分解的基础上.因此,计算可决系数首先需要对总离差平方和的分解有所了解.
1、总离差的概念.总离差就是因变量的实际观测值与其样本均值的离差即
2、总离差的分解.总离差可以分解为两部分:
对任一实际观测值总有:

总离差、解释离差和残差三者之间的关系如图2所示.

图2 总离差分解图
对公式(9)两边平方并求和,得:

如果用符号SST表示总离差平方和,用SSR表示解释离差平方和,用SSE表示剩余残差平方和,即:

则有:

将式(10)等号两边同除以 ,得:
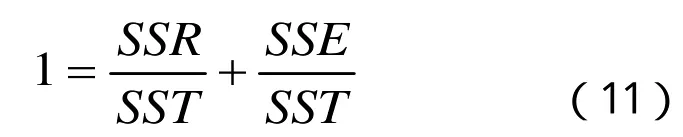
从式(11)中可以明显看出,各个样本观察点与样本回归直线靠得越近,SSR在SST中所占的比重越大.因此,如果用代表可决系数,可以将可决系数定义如下:

可决系数R2是对回归模型拟合程度的综合测量,可决系数越大,回归模型拟合程度越高;反之,回归模型拟合程度越差.
为剔除变量个数对拟合优度的影响,将残差平方和与总离差平方和分别除以各自的自由度,得到调整的可决系数记为,则有[13]:
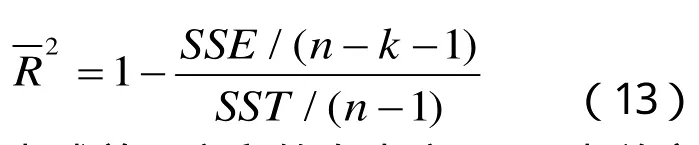
其中n-k-1为残差平方和的自由度,n-1为总离差平方和的自由度.
在实际拟合工作中,对曲线进行了拟合或找到了参数仅是完成了一部分工作,还必须根据拟合结果,如拟合报表,结合专业知识,对拟合作出正确的解释.不论是线性拟合还是非线性拟合,对其拟合结果的解释基本相同,通常是根据拟合的调整的可决系数、加权卡方检验系数及对拟合结果的残差分析而得出拟合结果的优劣的.文章对粗糙目标表面散射特性建模就是通过求解判断拟合程度优劣最常用的数量指标——调整的可决系数来反映所采用的BRDF模型的拟合程度的.调整的可决系数其值在0~1之间变化越接近1表明拟合效果越好,越接近0表明拟合效果越差[14].
3 粗糙目标表面BRDF模型优化
3.1 水泥板表面的BRDF模型验证
3.1.1 二参量模型拟合


图3 二参量模型对水泥板表面的拟合

表1 二参量模型对水泥板表面的拟合
利用二参量模型对水泥板数据进行拟合,入射天顶角 θi为0°、10°,如图3所示.图3中离散点是实测数据[15],曲线是其用二参量模型拟合的结果.拟合获得的模型参数如表1所示.从图3、表1中可以看出模型拟合效果都很好,这是因为水泥板是大粗糙度随机样片,光散射特征接近于朗伯面,可认为基本由漫反射组成,镜向分量可近似为零[15].
3.1.2 三参量模型拟合
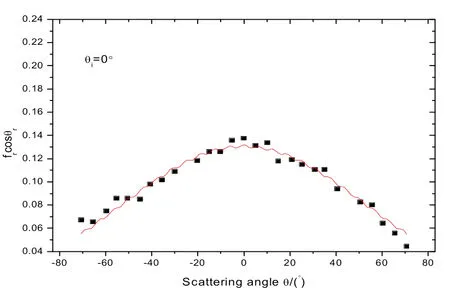

图4 三参量模型对水泥板表面的拟合

表2 三参量模型对水泥板表面的拟合
3.1.2 四参量模型拟合

图5 四参量模型对水泥板表面的拟合

表3 四参量模型对水泥板表面的拟合
3.2 花岗岩表面的BRDF模型验证
花岗岩表面颜色多样,并经过抛光处理后均匀粗糙.它是一种深成酸性火成岩,主要成分是[16].下面根据一组实验数据[16]对花岗岩表面0.6328um、入射天顶角为30°时的实验数据分别采用三种简化模型进行拟合,如图6、图7、图8所示.图中离散点是实测数据[16],曲线是其拟合结果.拟合获得的模型参数如表4所示.结果表明,二参量、三参量模型对花岗岩表面拟合结果都不是很理想,原因在于这两种模型没有考虑镜向分量.指数函数与漫反射函数的组合可以反映具有方向性的样片表面,所以四参量模型对经过抛光处理后的花岗岩表面拟合效果也是比较好的.
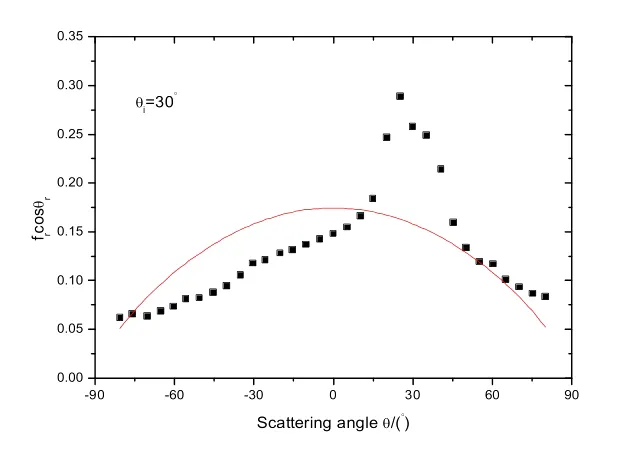
图6 花岗岩入射天顶角为30°的二参量模型拟合

图7 花岗岩入射天顶角为30°的三参量模型拟合
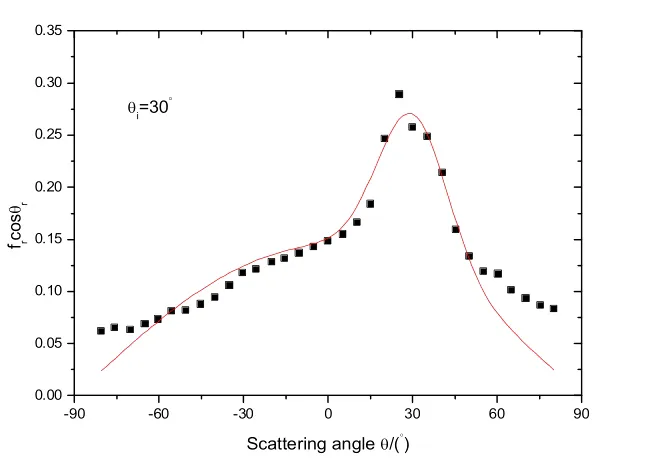
图8 花岗岩入射天顶角为 的四参量模型拟合
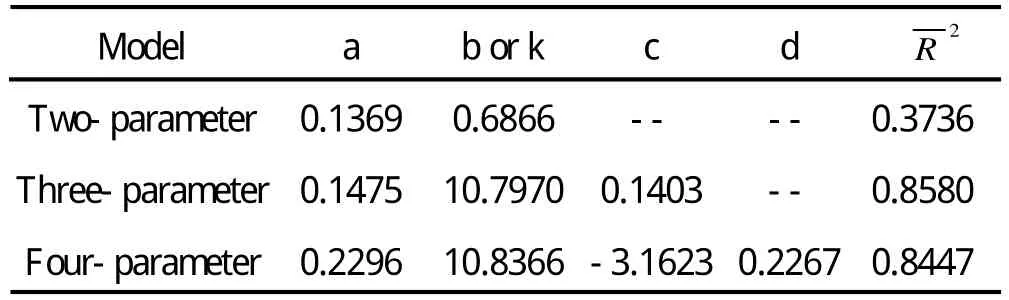
表4 花岗岩入射天顶角为 的四参量模型拟合
4 结论
本文采用从五参量模型简化而来的三种模型对文献[15-16]中的水泥板、花岗岩实测数据进行拟合并作了比较.结果表明,三种简化模型对表面粗糙的水泥板的拟合结果与实测数据吻合度都很高,但对经过抛光处理的具有方向性的花岗岩表面只有三参量和四参量模型的拟合效果较好,这说明简化模型的选择跟目标样片表面粗糙度有关.验证了简化模型的正确性,这为粗糙目标散射特性的分析简化了计算,节约了时间,为进一步作相关的多光谱成像研究与仿真奠定了基础.
[1] F.E.Nicodemus.Reflectance Nomenclature and Directional Reflectance and Emissivity[J].Applied Optics, 1970, 9(6):1474-1475.
[2] Wu Zhensen, Dou Yuhong.Visible light scattering and infrared radiation of spatial object[J].Acta Optica Sinica,2003, 23(10):1250-1254.
[3] Robert L.Cook,Kenneth E.Torrance.A reflectance model for computer graphics[J].ACM Transactions on Graphics, 1982,1(1): 7-24.
[4] 吴振森,韩香娥,张向东等,不同表面激光双向反射分布函数的实验研究[J].光学学报.1996.22(3):262-268.
[5] 张百顺,刘文清,魏庆农等.典型目标的BRDF实验室测量与模型验证[J].量子电子学报,2006,23(4):533-536.
[6] FLABBY F T.MOORE R K, FUNG A K.Microwave remote sensing[M].New York:Addison Wesley,1982.
[7] 孙成明,张伟,王治乐.双向反射分布函数在空间目标可见光反射特性建模中的应用[J].光学技术, 2008,34(5):750-757.
[8] 齐超,杨茂华,孙晓刚等.双向反射分布函数的测试方法分析和实验研究[J].中国激光,200330(Supp.):146-148.
[9] 姚连兴, 仇维礼, 王福恒.目标与环境的光学特性[M].北京:宇航出版社, 1995.
[10] 李良超, 吴振森, 杨瑞科等.基于神经网络的粗糙表面双向反射分布函数建模[J].应用光学, 2008, 29(3):448-451.
[11] 曹运华, 吴振森, 张涵璐等.粗糙目标样片光谱双向反射分布函数的实验测量及其建模[J].光学学报,2008, 28(4):792-797.
[12] http://course.cau-edu.net/course/z0193/ch08/se02/content/index.html.
[13] 李子奈,潘文卿著.计量经济学(第三版)北京.高等教育出版社.2010.3:73~75.
[14] 方安平, 叶卫平等著.Origin 8.0 实用指南.北京.机械工业出版社.2009.1:183~184,254.
[15] 吴振森, 谢东辉, 谢品华等.粗糙表面激光散射统计建模的遗传算法[J].光学学报, 2002, 22(8): 897-901.
[16] 谢鸣, 黄勇, 王晓春等.典型建筑外饰表面BRDF的实验研究[C].中国工程热物理学会学术会议论文.
BRDF-Based Statistical Modeling and Verification of Rough Target Surface
ZENG Jian-hua, ZHU Yun-dong, FANG Yu-ping, LIU Wei,DUAN Jian-jin, LI Ze-dong, LI Hong-ning, YANG Wei-ping
(Department of Physics,Yunnan Normal University,Kunming 650092,China)
In this paper, a BRDF five-parameter mo del is simplified as two-parameter model, three-parameter model and four-parameter model.The experimental data of the cement board and moorstone is fit with the simplified models.By comparison with the measured data, the results show that the two-parameter model are entirely feasible and effective for the target surface roughness BRDF statistical modeling, but not applying for the small target surface roughness.The threeparameter model and the four-parameter model can get a better fitting result for a variety of sample surface.The accuracy of the simplified model for the statistical modeling of rough target surface can simplify the calculation, save time and facilitate further the research of multi-spectral imaging and simulation related to the rough target
bidirectional reflectance distribution function(BRDF); rough target surface; simplified model
Q631
A
1008-9128(2012)02-0018-05
2011-08-20
国家自然科学基金项目(60968001,60768002),云南省自然科学基金项目(2009CD047),云南省大学生创新实验项目(CX07).
曾建华(1978- ),男,江西赣州人,硕士研究生.研究方向:多光谱成像技术研究.
杨卫平(1958- ),男,昆明人,云南师范大学教授.研究方向:颜色科学、多光谱成像技术等.
[责任编辑 张灿邦]

