随机电磁涡旋光束传输过程中斯托克斯参量和偏振度的变化

杨先才，丁攀峰，王燕飞

（华侨大学 信息科学与工程学院，福建 厦门 361021）

随机电磁涡旋光束传输过程中斯托克斯参量和偏振度的变化

杨先才，丁攀峰，王燕飞

（华侨大学 信息科学与工程学院，福建 厦门 361021）

基于交叉谱密度矩阵理论及其传输规律，推导随机电磁涡旋光束在自由空间中传输时的广义斯托克斯参量和偏振度的公式，分析相干长度对广义斯托克斯参量和偏振度的影响.研究结果表明：相干长度越长，即相干度越高，光束的涡旋特性越容易保持；随着相干长度的增加，斯托克斯参量和偏振度增加的比较缓慢；当相干长度远大于光斑尺寸时，广义斯托克斯参量和偏振度基本保持不变.

电磁涡旋光束；广义斯托克斯参量；偏振度；交叉谱密度；相干长度；自由空间

部分相干高斯－谢尔模型光束在相干理论研究中起着非常重要的作用［1-3］.1992年，Allen等［4］提出了涡旋光束，其所携带的轨道角动量可以传递给微粒，还可以实现对微米、亚微米微粒的俘获、平移，因而在粒子囚禁与操控等方面具有很重要的用途［5］.另外，涡旋光束在信息编码上也有较大的应用前景，利用涡旋光束的轨角动量可对信息进行编码与传输［6］.研究表明，偏振度在自由空间中传输时会发生变化.1852年，Stokes提出了以他名字命名的4个斯托克斯参量，每个参量都是位置的函数［7］.Wolf等［7-8］提出了随机光束的相干和偏振的统一理论.其重要的工具就是交叉谱密度矩阵，而矩阵中的每个矩阵元都是取决于空间中可以测量的一对位置点［8］.不同于斯托克斯参量，矩阵元严格遵守传播规律，可用来研究光束在传输过程中的偏振变化.此外，Korotkova推导了随机电磁光束在自由空间中的传播守恒定律［9］.本文利用统一理论和交叉谱密度传输理论，阐述并验证了随机电磁涡旋光束在自由空间中传输时广义斯托克斯参量和偏振度的行为特性.

1 理论分析与随机电磁光束公式推导

假设在源平面z＝0处，一束随机电磁涡旋光束旁轴在近似条件下沿着z轴正方向传输.在z＝0平面内，光束的二阶相干特性用2×2交叉谱密度矩阵［10］表述为

其矩阵元为

式（2）中：r1，r2为光源平面的二维位置矢量；ω为光束角频率；E（r，ω）为光源频率为ω的平面光束在r处的电场分量；＊表示空间－频率域内的复共轭；〈〉表示空间－频率域内的系综平均.

讨论的光源光束是取一特定的波长作为研究对象，故与角频率ω有关的方程不再显示ω.

根据广义的惠更斯－菲涅耳原理，光束在自由空间中传输一段距离（z＞0）后，光场的交叉谱密度函数［11］可以表示为

式（3）中：k＝2π／λ，λ为入射光的波长；ρ1，ρ2为目标平面的二维位置矢量；z为播距离.

假设在源平面处，随机电磁涡旋光束的电场矢量是带有涡旋项的拉盖尔-高斯模型［12］，即有

式（4）中：Ei，0和σi，0分别为源平面上光束的场辐射和光斑大小；r是位置矢量r的模；βi为光束的初相位；mi为涡旋光束的拓扑电荷数，为研究的方便取mi＝1.

通过以上的假设和推导，将式（4）代入式（2）中，可以得到在源平面处交叉谱密度矩阵元，即

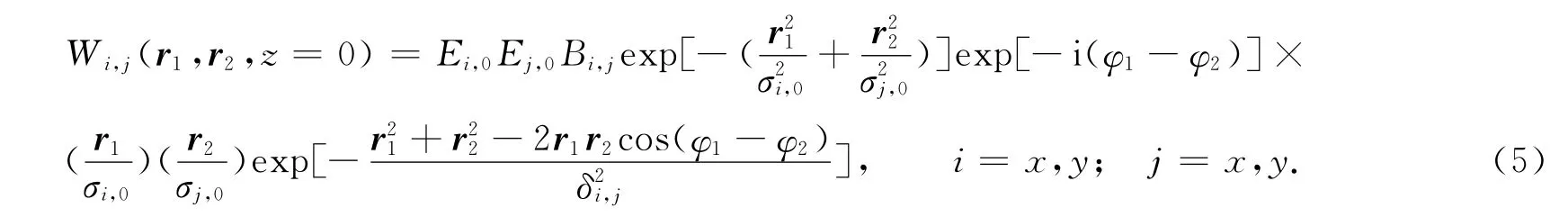
式（5）中：φ1，φ2和δi，j是方位角；δi，j是相干长度.Ei，0，Bi，j，σj，0与δi，j位置无关，但是与角频率ω 有关，与此同时，其中的一些量满足文献［13］中公式.把式（5）代入式（3），并且利用如下公式［14-15］，即

经过一系列的复杂的计算，可以得到目标平面处部分相干涡旋光束的交叉谱密度矩阵元.即

令ρ1＝ρ2＝ρ，θ1＝θ2＝θ，可以得到在目标平面上斯托克斯参量（包括光强）的表达式为

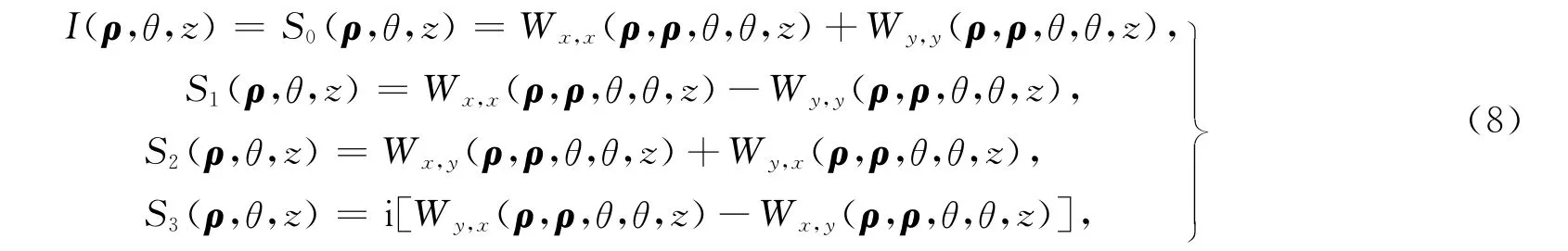
以及偏振度的表达式为

由式（8），（9）便可以计算在目标平面上的光强分布、斯托克斯参量和偏振度.

下面利用数学工具MathCAD进行数值模拟计算，研究相干长度对计算结果的影响.同时，利用试验条件下的结果和数值模拟的结果进行比较，检验二者的吻合程度.验证的实验装置图如图1所示.

从图1可知，由He－Ne激光器发射的高斯光束经过旋转的毛玻璃后形成部分相干光束，当光束经过螺旋相位板时，便可以获得部分相干涡旋光束，最后由电荷耦合元件（CCD）获得实验图像.

图1 实验装置Fig.1 Experiment setup

2 斯托克斯参量和偏振度的数值计算

利用数学工具 MathCAD并结合式（8），（9），对目标平面上的光强，斯托克斯参量和偏振度做数值计算.计算时，光斑大小固定取σx，0＝σy，0＝σ＝1mm，入射光波波长固定取λ＝632.8nm，而x和y方向上的电场强度分别取Ex＝1，Ey＝0.8.

在z＝1.5m处的固定平面上，不同相干长度归一化后的光强分布，如图2所示.从图2可知，相干度越高，横截面上的光强中心强度会减弱，并且随着相干度的增加，中间会出现暗核.也就是说，相干长度越高，光束的涡旋项越容易保持.

在z＝1.2m处，不同相干度下的光强分布实验图，如图3所示.在实验操作中，相干度近似用可见度表示，即利用V＝（Imax－Imin）／（Imax＋Imin）来计算，而相干度的大小则是通过改变毛玻璃的位置来调节的.将图3和图2进行比较可以知道：实验所得的光强分布与归一化的光强剖面曲线图相似，中心出现暗核，并且当相干度越高时，在同一地点的光强也越强，光强亮暗的对比也越明显.总体来说，实验结果和数值模拟的结果大致吻合.

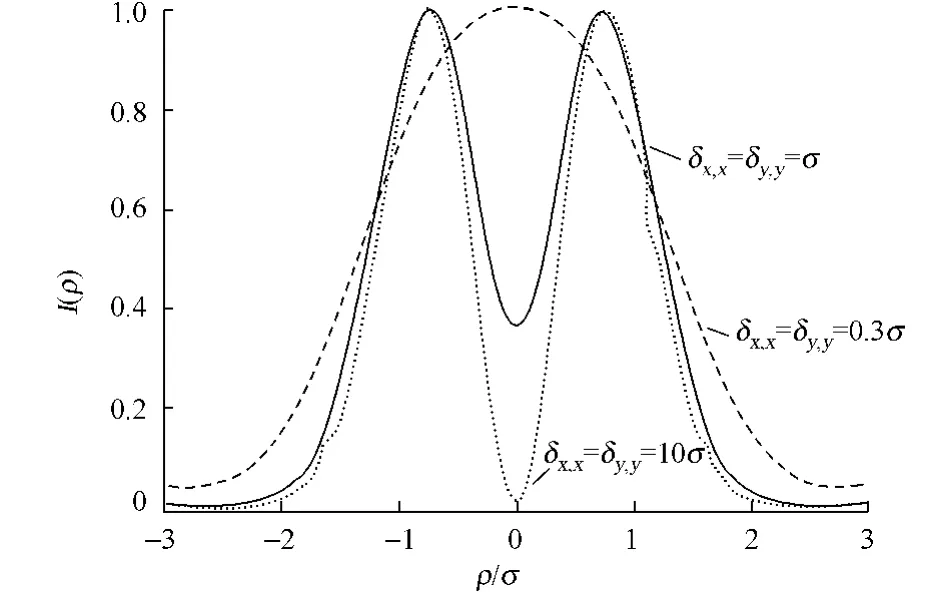
图2 不同相干长度的归一化光强剖面曲线Fig.2 Curves of the normalized intensity profiles for different coherence lengths

图3 不同相干长度的光强分布实验图Fig.3 Intensity distribution of experimental results for different coherence lengths

在不同的相干长度下沿着z轴传输时轴上点光强分布的变化情况，如图4所示.从图4中曲线a可看出，轴上点光强S0的分布是随着传输距离的增加而单调降低直至降为零；从图4中曲线b可看出，轴上点光强S0的分布先短暂增加，达到最大值后开始降低，直到降为零；从图4中曲线c可看出，轴上点光强S0的分布也是先增加后降低，但比较而言，要变化得慢一些.

为了证实光强分布随着传输距离的变化情况，实验测量当相干长度为δx，x＝δy，y＝0.3σ（旋转毛玻璃处于合适的位置）时，不同距离情况下的光强分布光斑图，如图5所示.从图5中可以看出，随着传播距离每40cm的增加，光强的分布变得越来越弱，而且光斑有扩散的趋势.这与图4中曲线a的光强分布随着传输距离的增加而减弱的情况类似，说明实验结果与理论假设基本符合.

取Bx，y＝0.3exp（－i（π／6）），通过数值模拟轴上点在传输过程中随机电磁涡旋光束的相干长度对广义斯托克斯参量和偏振度的影响，如图6，7所示.在此为讨论方便，定义归一化的斯托克斯参量为sa（a＝1，2，3）和S0的比值.

图4 轴上点光强分布随着传输距离的变化Fig.4 Changes in the intensity distribution for different coherence length on axis along the Z－axis

图5 不同距离处的光强分布光斑图Fig.5 Changes of experimental measurement in the intensity distribution for different positions

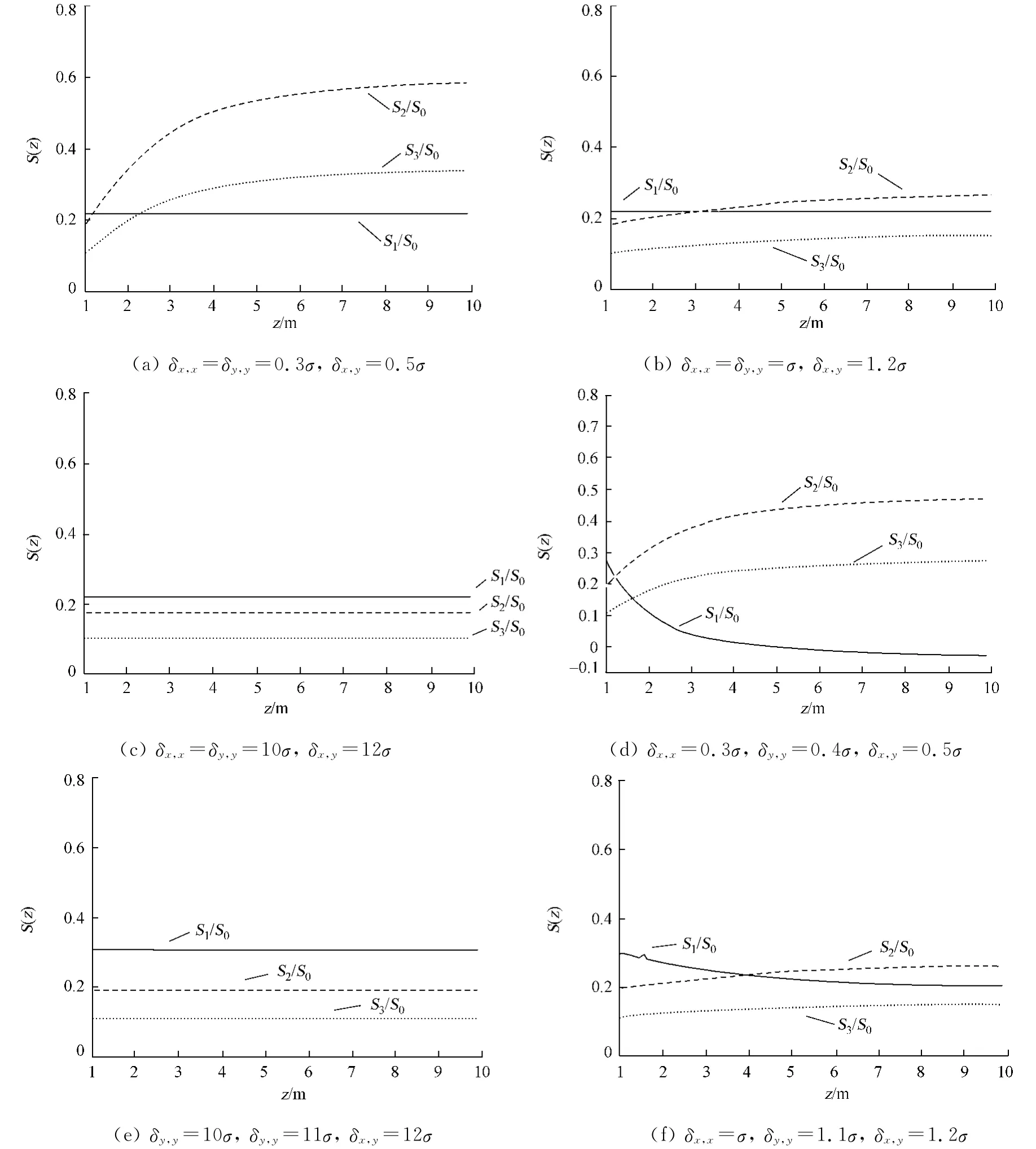
图6 相干长度对归一化斯托克斯参量的影响Fig.6 Influence of normalized Stokes parameters for coherence lengths

图7 相干长度对偏振度的影响Fig.7 Influence of the degree of polarization for coherence lengths

从图6（a）～（b）可以明显看出，当x向相干长度和y向相干长度相等但远远小于光斑尺寸时，随着传播距离的增加，2个归一化的斯托克斯参量S2／S0和S3／S0都是分别单调增加到一个固定的值并保持不变，只是图6（b）中的变化比图6（a）要缓慢一些，而S1／S0则随着传播距离的增加都基本上保持不变.从图6（c）可以看出，当相干长度远远大于光斑尺寸时，3个归一化的斯托克斯参量随着传播距离的增加都基本上保持不变.

从图6（d）中可以看出，与图6（a）最大的不同是S1／S0由正值下降到零直至负值，并最终保持恒定值不变.这是由于在源平面有 Wx，x＞Wy，y，但是随后 Wx，x下降得比 Wy，y快，这当中会出现 Wx，x＝Wy，y（例如S1＝0）.在图6（e）中，2个归一化的斯托克斯参量S2／S0和S3／S0单调增加到一个最大值然后保持不变，但是S1／S0单调减小直至最小值然后保持不变.在图6（f）中，3个归一化的斯托克斯参量基本保持不变.

从图7（a）可知，偏振度曲线a，b分别单调增加到一个固定的值并保持不变，而偏振度曲线c基本上保持不变.从图7（b）可知，偏振度P曲线a先减小到一个最小值后开始增加，但是偏振度P曲线b，c基本上保持不变.

3 结论

理论分析并推导了随机电磁光束公式，研究并实验验证随机电磁涡旋光束在自由空间中传输时广义斯托克斯参量和偏振度的行为特性.由于涡旋光束在x向和y向上的相干性强弱并不十分明确，分别作了讨论并最终呈现出不同的变化分布.

通过研究得到无论x向相干长度是否等于y向相干长度，都有以下几点主要结论：1）相应的归一化的斯托克斯参量S2／S0和S3／S0的变化基本一致；2）随着相干长度的增加，归一化的斯托克斯参量和偏振度的变化越来越不明显，后来基本保持不变；3）变化最大的是S1／S0，即当x向相干长度等于y向相干长度（图6（a），（b））时，S1／S0保持不变，而当x向相干长度不等于y 向相干长度（图6（d），（e））时，S1／S0出现下降的变化；4）正是由于S1／S0的不同变化，使得P曲线a出现了相应的不同变化.

鉴于部分相干光束在遥感、跟踪和远距离通讯等应用中具有独特的优势，以及光的偏振性在光学检测、显示技术、数据存储、光通信、材料科学等方面的广泛研究与应用，使得实验结论对于随机电磁涡旋光束传输的偏振态研究具有一定的借鉴和指导意义.

［1］MANDEL L，WOLF E.Optical coherence and quantum optics［M］.Cambridge：Cambridge Univ Press，1995.

［2］COLLETT E.Polarized Light：Fundamentals and applications［M］.Florida：CRC Press，1992.

［3］BORN M，WOLF E.Principles of optics［M］.Cambridge：Cambridge Univ Press，2005.

［4］ALLEN L，BEIJIERSBERGEN M W，SPREENUW R J C，et al.Orbital angular momentum of light and the trans－formation of Laguerre－Gaussian laser modes［J］.Phys Rev A，1992，45（11）：8185－8189.

［5］HE H，FRIESE M E，HECKENBBERG N R.Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity［J］.Phys Rev Lett，1995，75（5）：826－829.

［6］BOUCHALl Z，CEL ECHOVSKY R.Mixed vortex states of light as information carriers［J］.New J Phys，2004，6：131.

［7］WOLF E.Introduction to the theory of coherence of polarization of light［M］.Cambridge：Cambridge Univ Press，2007.

［8］KOROTKOVA O，WOLF E.Generalized Stokes parameters of random electromagnetic beams［J］.Opt Lett，2005，30（2）：198－200.

［9］WOLF E.Unified theory of coherence and polarization of random electromagnetic beams［J］.Phys Lett A，2003，312（5／6）：263－267.

［10］WOLF E.Correlation－induced changes in the degree of polarization，the degree of coherence，and the spectrum of random electromagnetic beams on propagation［J］.Opt Lett，2003，28（13）：1078－1180.

［11］KOROTKOVA O.Conservation laws for stochastic electromagnetic free fields［J］.J Opt A：Pure Appl Opt，2008，10（2）：025003.

［12］MALEEY I D，PALACIOS D M，MARATHAY A S，et al.Spatial correlation vortices in partially coherent light theory［J］.Phys Rev Lett，2004，21（11）：1895－1900.

［13］CHEN Zi－yang，PU Ji－xiong.Stochastic electromagnetic vortex beam and its propagation［J］.Phys Lett A，2008，372（15）：2734－2740.

［14］RAO Lian－zhou，PU Ji－xiong.Formation of small bottle light beams［J］.Chin Phys Lett，2007，24（12）：3412－3415.

［15］GRADSTEYN I S，RYZHIK I M.Table of Integrals series and products［M］.California：Academic Press，1980.

Changes in Stokes Parameters and Degree of Polarization of Stochastic Electromagnetic
Vortex Beams on Propagation

YANG Xian－cai，DING Pan－feng，WANG Yan－fei
（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

Based on the theory of cross－spectral density matrix and the propagation laws of cross－spectral density，the general formulae were derived to calculate the generalized Stokes parameters and degree of polarization for a class of stochastic electromagnetic vortex beam while propagating in free space.Meanwhile，the influence on propagation of the generalized Stokes parameters and the degree of polarization by the coherence length was analyzed.It is shown that the higher the correlation length（the higher the degree of coherence）is，the better the vertical component can keep；the Stokes parameters and the degree of polarization increase more slowly with the increment of the correlation length increase；the generalized Stokes parameters and the degree of polarization keep almost invariant while the coherence length is much larger than beam size.

stochastic electromagnetic vortex beam；generalized stokes parameters；polarization′s degree；cross－spectral density；free space；coherence length

钱筠 英文审校：吴逢铁）

O 436.1

A

1000－5013（2012）01－0017－06

2011－05－19

丁攀峰（1980－），男，副教授，主要从事光束传输和偏振光学的研究.E－mail：dingpf＠hqu.edu.cn.

国家自然科学基金培育项目（JB－ZR1126）；福建省厦门市科技计划项目（3502Z20113017）