广义Lorenz系统的Painlevé分析及其精确解
陈南,张金顺
(华侨大学 数学科学学院,福建 泉州 362021)
广义Lorenz系统的Painlevé分析及其精确解
陈南,张金顺
(华侨大学 数学科学学院,福建 泉州 362021)
考虑一个Hamilton函数为H=-σxy+rxyu+-βuz的四维广义Lorenz系统,利用Painlevé分析的方法,将该系统进行奇异流型展开.利用调谐因子项将其进行有限项“截断”,证明其具有Painlevé可积性,并导出其自Bäcklund变换和奇异流型满足的Schwarz导数方程.通过研究相关的Schwarz导数方程的性质,求出广义Lorenz系统的精确解.
广义Lorenz系统;Painlevé分析;调谐因子;Bäcklund变换;Schwarz导数
1 预备知识
混沌是非线性系统研究领域非常活跃的前沿课题[1].Painlevé方法已被广泛应用于探讨非线性微分方程的可积性,并被证明是一种十分有效的途径[2-10].将Lorenz系统推广为四维广义Lorenz系统,即
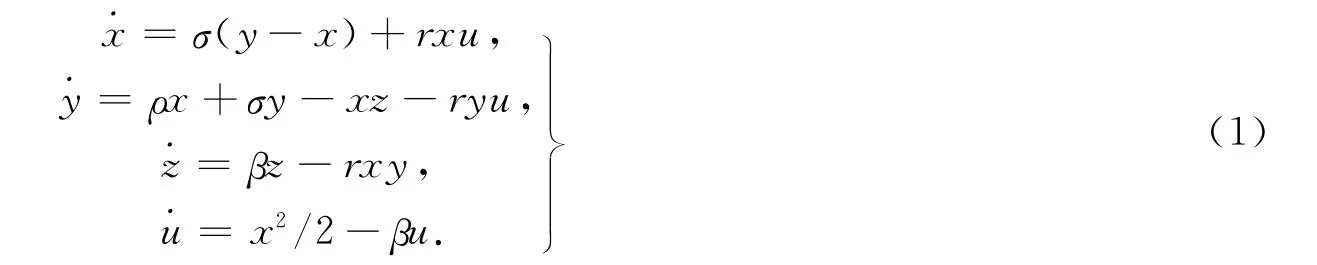
系统(1)中:σ,ρ,β,γ是常量;x,y,z,u 是自变量t的函数;˙x,˙y,˙z,˙u 分别表示x,y,z,u 关于t的导函数.这是一个2维Hamilton系统,即
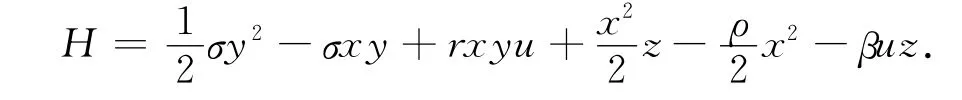
对x,y,z,u进行奇异流型展开,可得

式(2)中:φ为奇异流型.通过主导项分析得α1=α4=1,α2=α3;且有
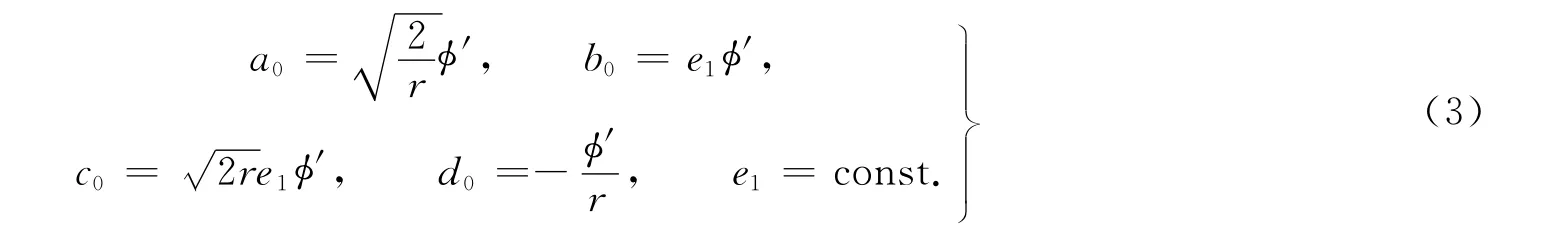
令α2=α3=1,即
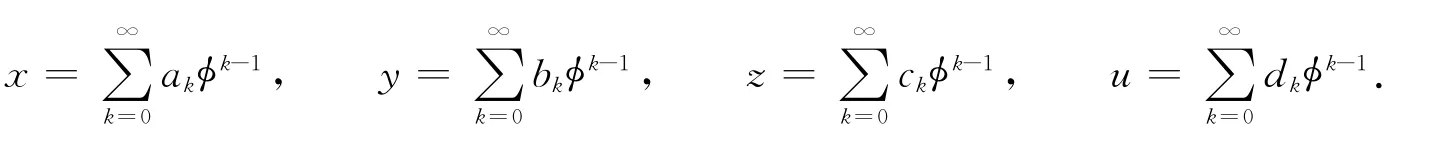
将其代入系统(1),有
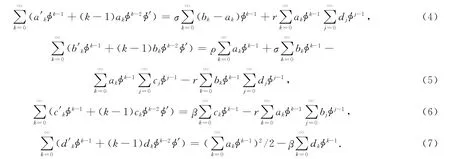
比较φ的同次幂系数,得
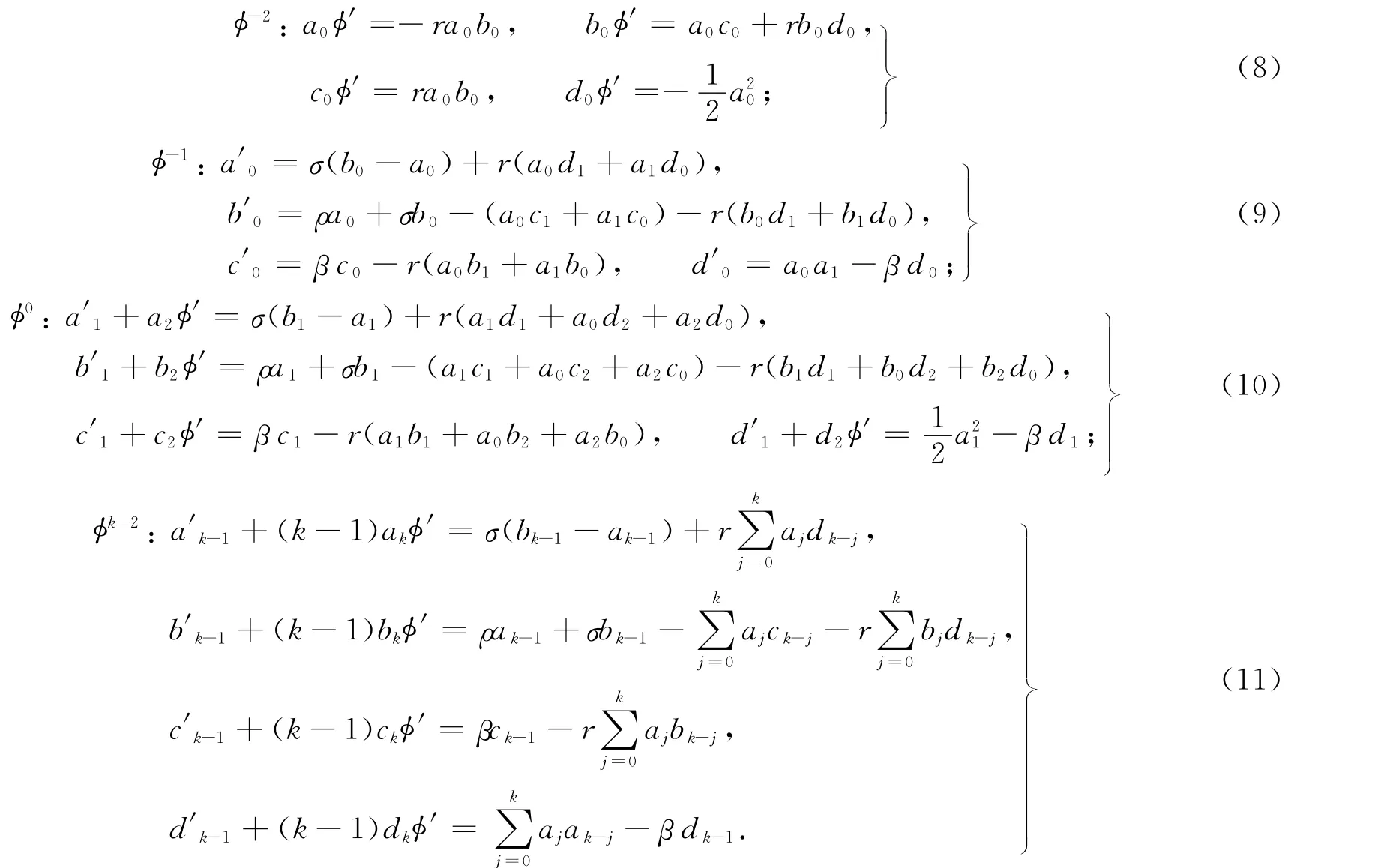
计算调谐因子,对式(11)移项可得
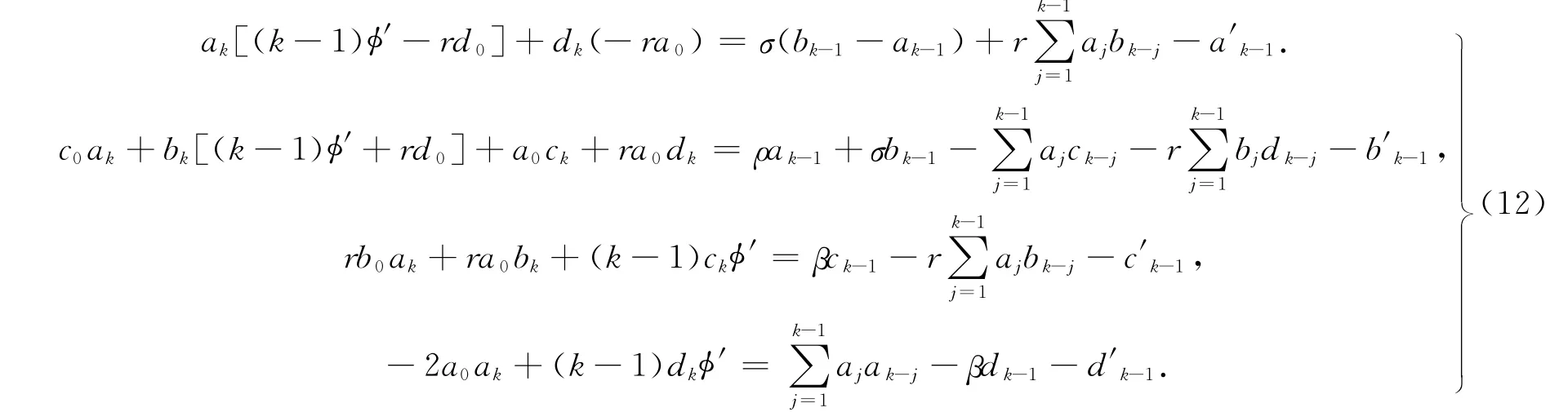
分别记式(12)中各个方程的右式为F1,F2,F3,F4,其中F1,F2,F3,F4为ak-1,bk-1,ck-1,dk-1,…,a0,b0,c0,d0,φ的函数.将式(3)代入式(12),转换成矩阵形式得
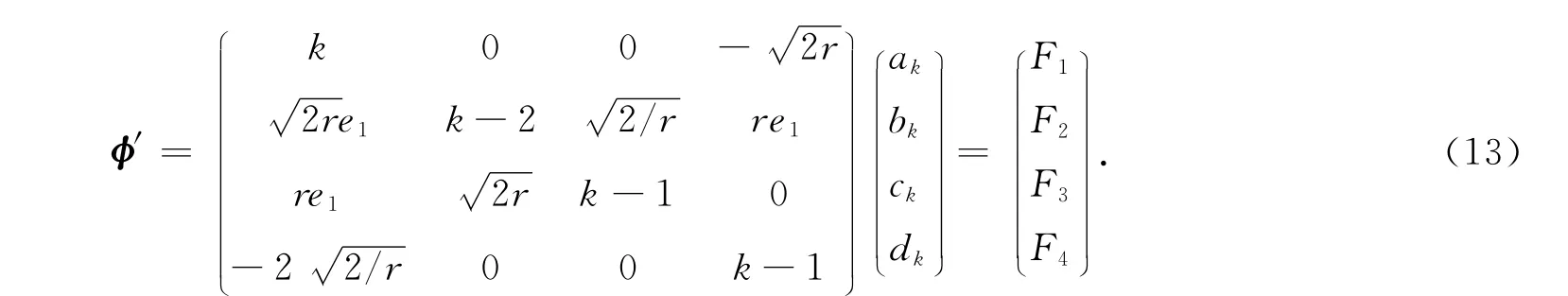
利用行列式计算调谐因子,可得
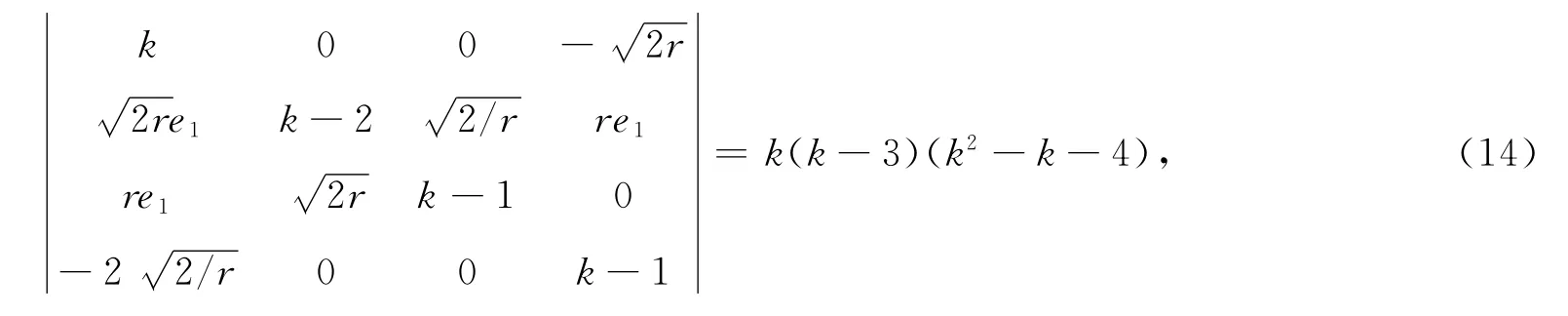
得到调谐因子k=0,3.若令a2=b2=c2=d2=0,经过计算可推出当j≥3时,aj=bj=cj=dj=0,即Painlevé奇异流型展式(2)被成功“截断”,从而该四维广义Lorenz系统(1)具有Painlevé可积性.
命题1 四维广义的Lorenz系统(1)有Bäcklund变换,即
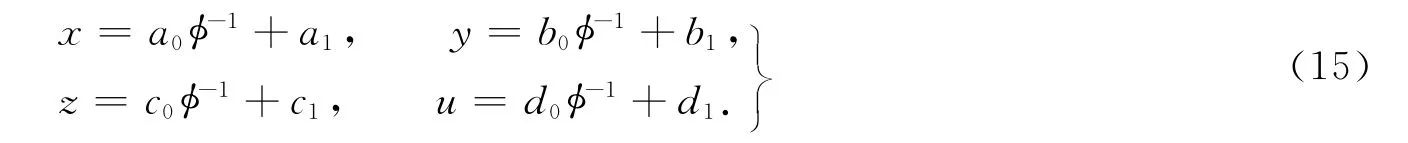
式(15)中,φ满足Schwarz方程
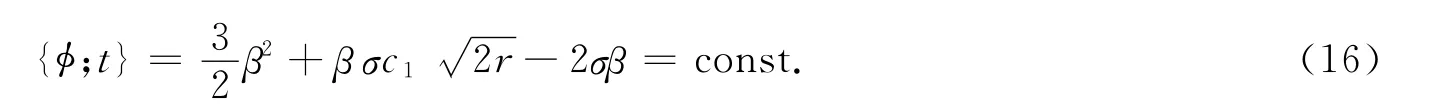
证明 利用式(8)~(10),经计算可得
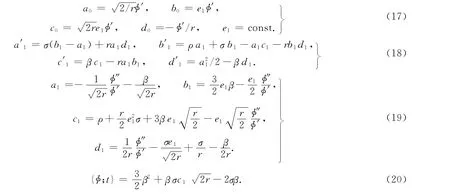
由式(18)可知:a1,b1,c1,d1满足系统(1),同时x,y,z,u 满足系统(1),故式(15)为系统(1)的自Bäcklund变换.
2 广义Lorenz系统的精确解
通过求解Schwarz导数方程,得到该系统的一个精确解.设+βσc1-2σβ=λ,则


1)当λ≥0时,从式(22)可求解得
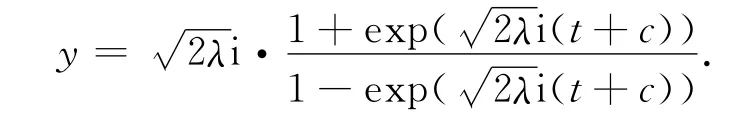
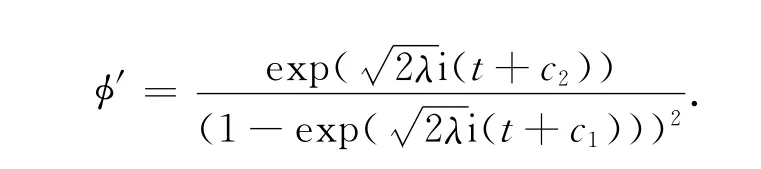
两边积分后,可得
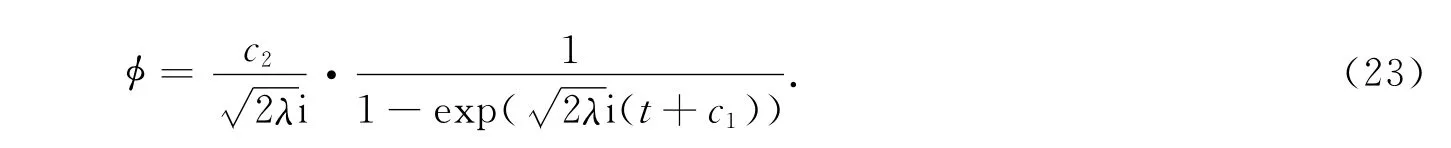
2)当λ<0时,从式(22)可求解为


式(26)中:φ已由上面解出.
[1]LORENZ E N.Deterministic nonperiodic flow[J].J Atmos Sci,1963,20(2):130-141.
[2]CLARKSON P A.The painleve equations-nonlinear special functions[J].J Comp Appl Math,2003,153(1/2):127-140.
[3]WEISS J.On classes of integrable system and the Painlevéproperty[J].J Math Phys,1984,25(1):13-14.
[4]WEISS J.TABOR M,CARNEVALE G.The Painlevéproperty of partial differential equations[J].J Math Phys,1983,24(6):522-526.
[5]楼森岳,唐晓艳.非线性数学物理方法[M].北京:科学出版社,2006.
[6]陈志雄.Painlevé性质与完全可积性[J].上海交通大学学报,1990,24(2):16-22.
[7]王鸿业,张桦.Henon-Heiles系统的Painlevé分析及其显示解[J].郑州大学学报:理学版,2005,37(4):14-16.
[8]梁小花,张金顺.一个N 维 Hamilton系统的Painlevé分析与精确解[J].华侨大学学报:自然科学版,2007,28(3):327-329.
[9]李金伟,张金顺.高阶Boussinesq-Burgers方程的Painlevé测试及其精确解[J].华侨大学学报:自然科学版,2010,31(2):227-229.
[10]邓勇,张金顺.高阶Levi方程的Painlevé测试和精确解[J].华侨大学学报:自然科学版,2009,30(4):476-477.
PainlevéAnalysis and Explicit Solutions for a Generalized Lorenz System
CHEN Nan,ZHANG Jin-shun
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)
A four-dimensional generalized Lorenz system with the Hamiltonian function is considerated.The system is studied by Painlevéanalysis method.The singular manifold expandation is finite“truncation”by means of resonances,and it is proved that the system is Painlevéintegrability.The self-Bäcklund transformation of the system is goten out.Some explicit solutions are obtained by means of the Schwarz derivative equation.
generalized Lorenz system;Painlevéanalysis;resonances;Bäcklund transformation;Schwarz derivative
钱筠 英文审校:黄心中)
O 175.3
A
1000-5013(2012)01-0094-05
2011-06-11
张金顺 (1956-),男,教授,主要从事孤立子理论与可积系统的研究.E-mail:jszhang@hqu.edu.cn.
国家自然科学基金资助项目(10871165);华侨大学高层次人才科研启动项目(07BS106)

