水下爆炸载荷的静态等效方法

边文凤， 苗会文， 白光辉， 程 杰

(1.哈尔滨工业大学(威海)土木工程系，山东 威海 264209;2.中复西港船艇有限公司，山东 威海 264209)

水下爆炸载荷的静态等效方法

边文凤1， 苗会文2， 白光辉1， 程 杰1

(1.哈尔滨工业大学(威海)土木工程系，山东 威海 264209;2.中复西港船艇有限公司，山东 威海 264209)

水下爆炸对水中结构物的作用一是直接压力，另一个是使结构物产生速度和加速度，而且，不仅仅是结构物产生速度和加速度，其附加质量(也称附连水质量)也产生相应的加速度，即:爆炸要同时改变结构物和附加质量的动能与动量。水下爆炸作用下结构物的响应研究极其复杂，计算量极大。如果能采用静态等效的方法分析结构的响应，不但使结构分析过程得到简化，更重要的是为结构设计提供一个等效载荷值和施加方法。根据能量原理、动量原理和达朗贝尔原理，给出了水下爆炸载荷静态等效研究的分析方法和计算方法，并通过算例对该算法进行了验证。结果表明:提出的静态等效方法可行。

水下爆炸;冲击波;静态;等效;载荷

0 引言

近年来，很多学者对船体在水下爆炸载荷作用下的响应进行了研究。文献［1－6］分别应用舰船非接触水下爆炸动力学理论、声固耦合算法、实验、有限元方法等方法研究了水下爆炸冲击作用下舰船的响应。爆炸冲击对舰船作用载荷极其复杂，现在仍然是该方向的研究重点及难点，至今尚无精确有效的描述方法。同时，爆炸载荷作用下的结构分析计算不仅复杂，对计算机的要求高，多数计算都要在工作站进行，而且，其计算理论与方法也比较难以掌握，更不便于结构设计时应用。鉴于上述原因，笔者依据能量原理、动量原理、d’Alember’s(达朗贝尔)原理和附加质量(附连水质量)原理等基本原理，建立水中结构物在受到水下爆炸冲击时所受载荷的静态等效研究方法。该方法可以极大地简化爆炸问题的结构分析，使计算量得到级数缩减，也为结构设计提供载荷分析的依据，从而提高设计效率。

1 基本原理方法

1.1 水下爆炸冲击波描述

海中水下爆炸产生以声速传播的冲击波，实测数据表明，压力值在从最大值下降到峰值三分之一的时间内，可以认为是按指数规律下降的。此后的时段，冲击波的衰减变慢，以近似于时间倒数的关系衰减。爆炸冲击波的特性如图1所示。

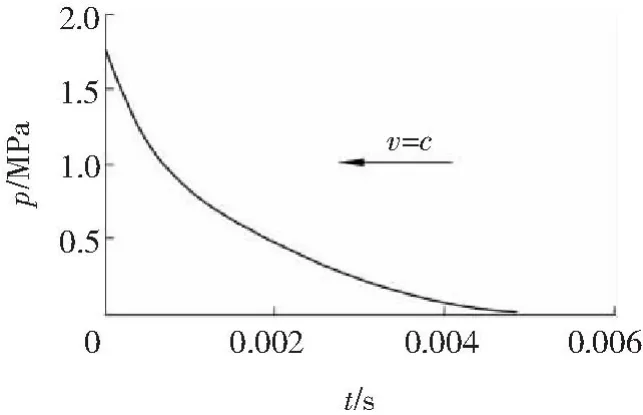
图1 以声速c传播的冲击波压力Fig.1 Shock wave pressure with sound velocity of c

通过大量的实验和爆炸相似率的分析，Cole和Zamyshlyayev［7］提出了较为完整的冲击压力公式:

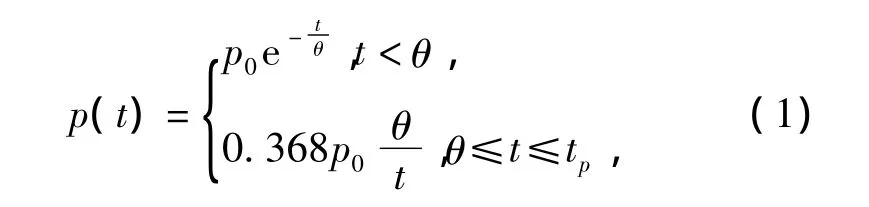
式中:p——冲击波压力;

p0——峰压;

t——时间;

θ——时间衰减常数;

tp——冲击正压力的作用时间，取tp=(150～200)θ。

冲击波峰压p0与炸药质量mT及爆心到目标的直线距离r之间的关系为

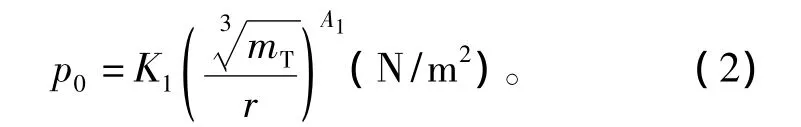
衰减常数θ的表达式:

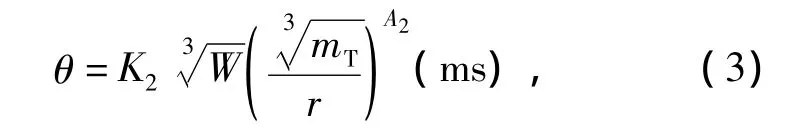
式中，K1、K2、A1、A2取决于炸药的类型。对 TNT 炸药，如果取国际单位制，则 K1=52.4，K2=0.084，A1=1.13，A2= －0.23。

1.2 水下爆炸后被冲击物体吸收的能量与冲量

水下爆炸冲击结构物，使结构物的动能、动量、变形能等都发生改变。结构物所吸收的能量和冲量可以分别由能量通量和冲量通量通过积分求得。能量和冲量可以用来估计物体被冲击后的初始速度和加速度。

1.2.1 爆炸后物体吸收的能量

能量通量［1］:

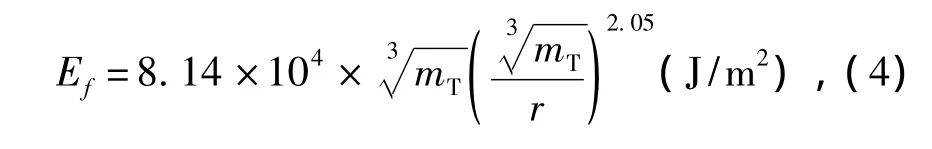
式中:Ef——能量通量。

对能量通量积分，得到能量总量:

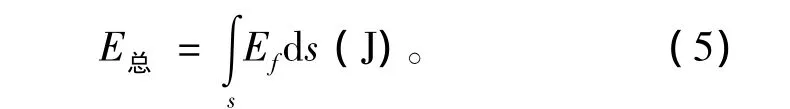
1.2.2 爆炸后物体吸收的冲量

冲量通量［1］:

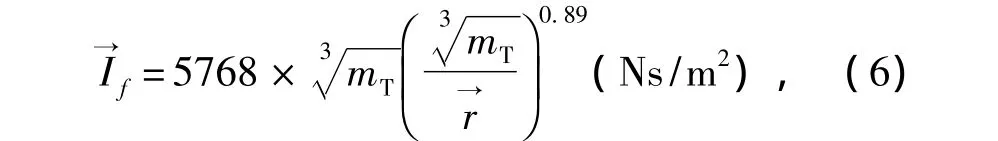
式中:Ix——物体水平方向的冲量值;

Iz——物体垂直方向的冲量值。

1.3 附加质量的计算

查表［9］可得不同σr和Λ下垂直和水平方向附加质量系数CV与CH，于是:

垂直方向附加质量:

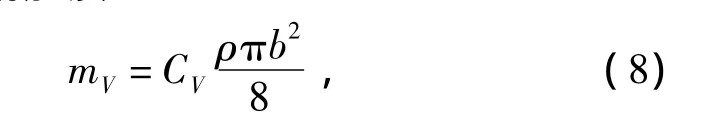
水平方向附加质量:

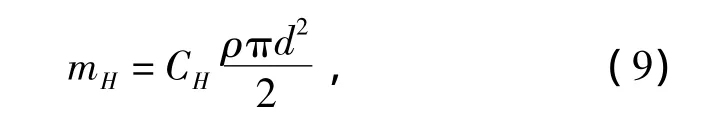
式中:ρ——水的密度。

1.4 水下爆炸后被冲击物体的速度与加速度计算［10］

1.4.1 爆炸作用时间

爆炸点到物体最近点和最远点的距离分别用r1和r2表示，c表示冲击波在水中的传播速度，则爆炸波到达最近点和最远点所需的时间分别为:t1=r1/c，t2=r2/c，冲击波持续作用时间为tp，故爆炸冲击波通过物体所耗时间为:t=t2－t1+tp。

1.4.2 垂直方向的速度与加速度

根据动量守恒定理:Iz=Mzgt+Mzvz，可得:

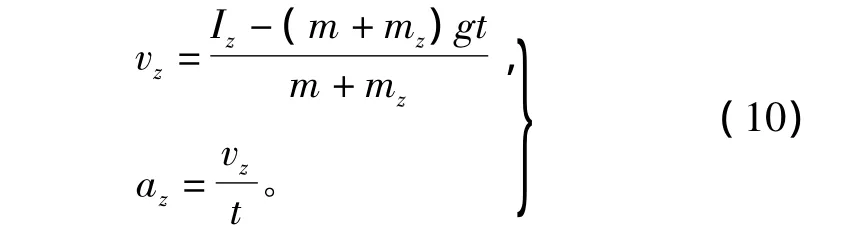
式中:Mz=m+mz;

mz——垂直方向附加水质量;

m——物体质量;

vz，az——物体垂直方向的速度、加速度。

1.4.3 水平方向的速度与加速度

根据动量守恒定理:Ix=Mxvx+Fxt，可得:

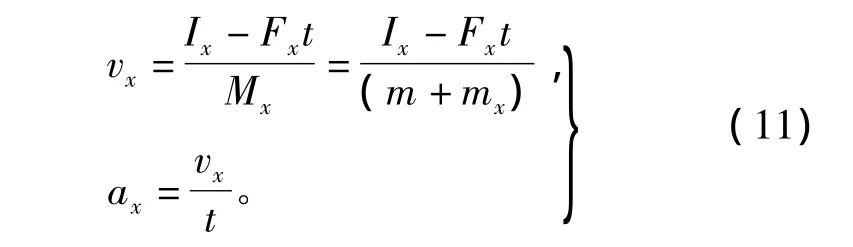
式中:Fx——物体背爆面的侧面水压力;

Mx=m+mx，mx为水平方向附加水质量;

vx，ax——物体水平方向的速度、加速度。

1.5 静态等效载荷分析［10］

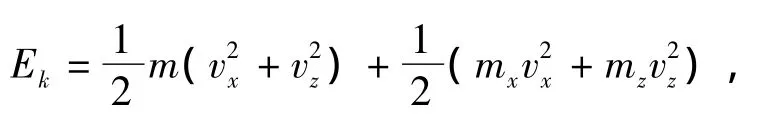
根据上述分析，由水下爆炸引起的作用于结构物的静态等效载荷分布情况为:受爆炸冲击的面上承受载荷pj、物体背爆面受到水体对其产生的阻力、在水平和垂直运动方向分别产生加速度ax、az;对于不受爆炸冲击作用的湿面，仅受静水压力作用。另外，物体还受到自身重力的作用。

2 算例与对比

根据上述原理，取一长方形壳体模型作为算例，进行正侧面爆炸研究。根据各项给定参数，利用MATLAB软件进行编程，分别计算炸药爆炸后长方壳体吸收的能量和冲量、垂直和水平运动方向的附连水质量、初始速度及加速度等，得到受爆炸冲击的长方壳体湿面上受到的等效静载荷分布情况。

利用MSC.PATRAN建立长方壳体的有限元模型，施加等效静载荷，背爆面两端约束，在Nastran求解器中进行静态分析计算，得出模型的位移和应力结果。同时，为了验证该等效方法的可行性，文中将建立长方形壳体及其周围流体的有限元模型，施加水下爆炸载荷，在Dytran求解器中进行动态分析计算，得出长方形壳体模型爆炸响应下的位移和应力。最后，将静态和动态分析结果进行对比分析，验证静态等效方法的可行性。

2.1 算例模型

长方形壳体模型如图2所示，其尺寸和材料参数见表1，壳体漂浮于水面上。球形TNT炸药包质量为mT=5 kg，炸药包位于壳体正前面5 m、水面以下h/2处，h为吃水深度，B为爆炸点。

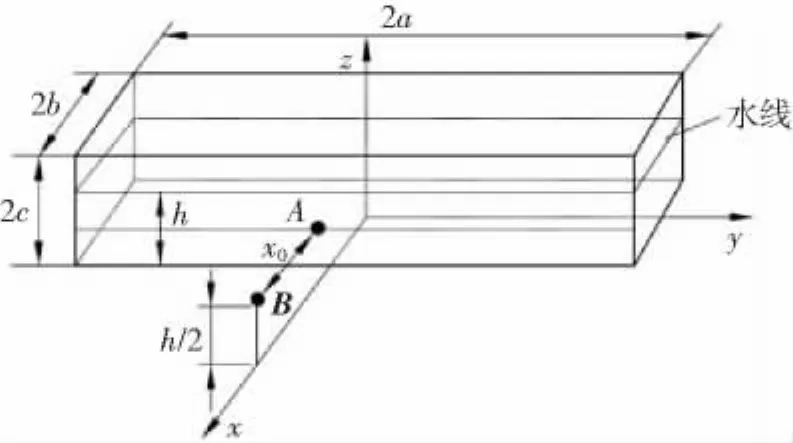
图2 长方形壳体模型Fig.2 Rectangular shell model

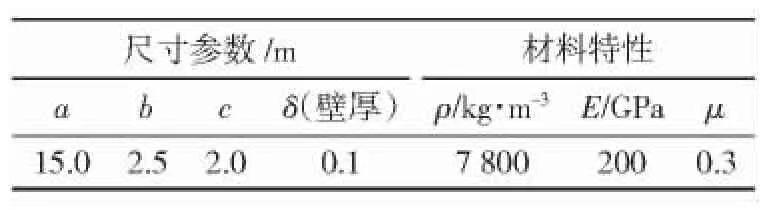
表1 模型参数Table 1 Parameters of model

2.2 静态等效载荷的计算

2.2.1 吃水、附加质量与能量

此算例中爆炸是在长方壳体的正前面实施，所以，只有壳体的正前面承受爆炸冲击并吸收爆炸产生的能量，壳体仅在水平方向运动。根据前述能量原理、动量原理、附加质量原理及计算方法，结合给定的模型初始条件，用MATLAB软件进行编程，求解计算静态等效载荷所需要的各项参数。此计算流程见图3，计算结果见表2。

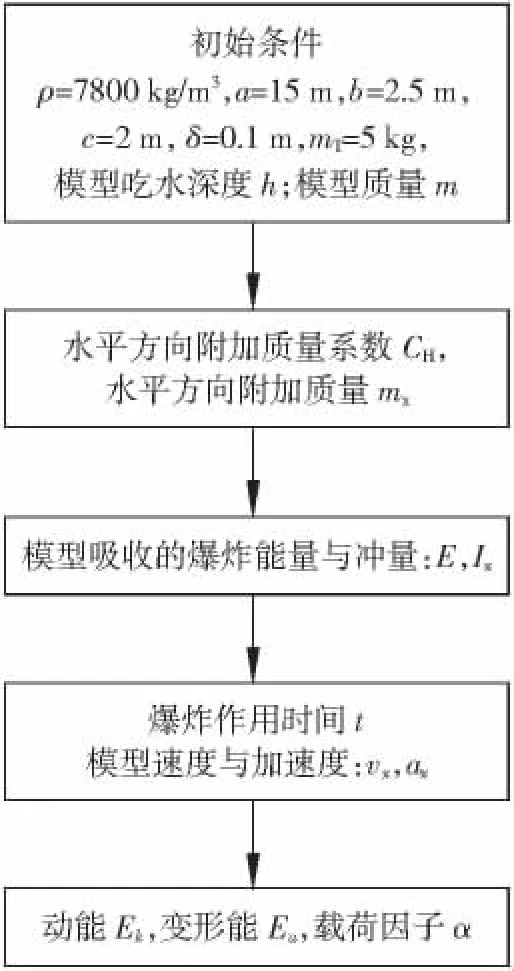
图3MATLAB计算流程Fig.3 Calculation flow chart in MATLAB

表2 参数计算结果Table 2 Parameter calculation results

2.2.2 静态等效载荷

(1)冲击载荷

质量为5 kg的球形TNT炸药爆炸后作用于长方体形壳上，静态等效载荷计算如下:

爆炸点B到前面上任一点(x，y，z)的距离为r。根据式(1)，计算得到0～tp时间段内冲击载荷平均值，即:

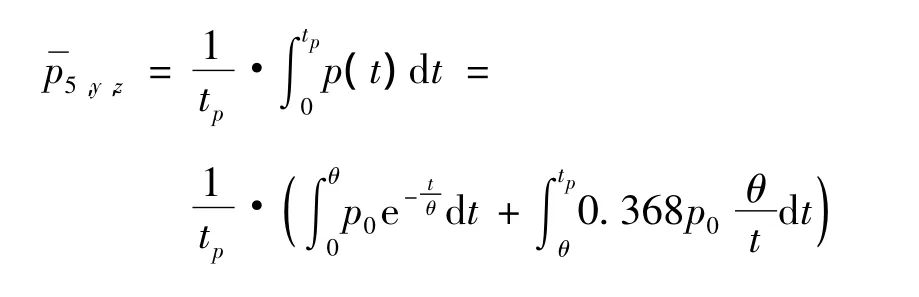
由于高度方向尺寸远小于长度方向，对于任意y，求出pj在z向的平均值:

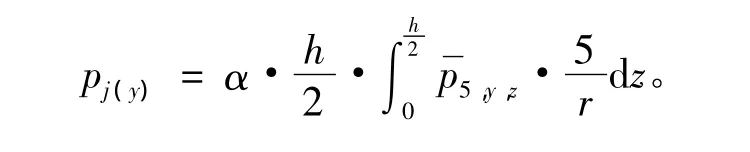
因此，在z方向可以用载荷平均值代替，而沿y方向则按计算所得的规律分布，如图4所示。

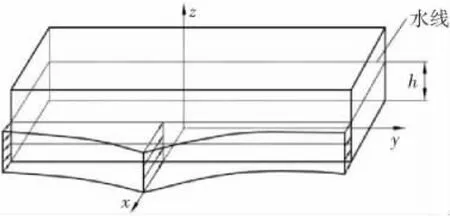
图4 静态载荷计算示意图Fig.4 Sketch map of static load calculation

(2)阻力与其他

壳体背爆面所受阻力，由附连水惯性力和静水阻力构成，考虑整体的动平衡，由达朗伯原理求出壳体背爆面所受的平均阻力:竖直方向重力加速度:g=9.8 m/s2，方向:+z;水平方向平均加速度:ax=1.696 0 m/s2，方向:－x;

左右侧面受静水压力:p+y=p－y=ρgh。

2.3 方法的验证

对上述模型，在MSC.Dytran中进行动态分析，在MSC.Nastran中将上述得到的静态等效载荷施加在模型上，进行静态分析，将两种分析得到的结果进行对比。

2.3.1 动态分析

在MSC.PATRAN中建立上述长方形壳体包括其周围流体的有限元模型，见图5。施加5 kg球形TNT炸药爆炸后产生的爆炸载荷，并利用MSC.Dytran求解器进行分析，得到模型在爆炸载荷下的位移和应力响应，图6～9分别表示模型的位移云图、应力云图、测点A(见图2)水平方向的位移和应力曲线。

图5 壳体与周围流体有限元模型Fig.5 Finite element model of shell and surrounding fluids

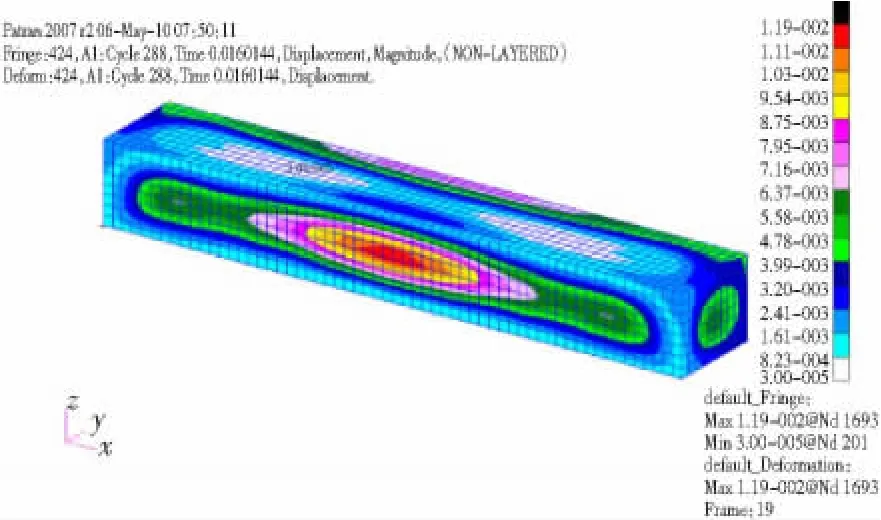
图6 模型位移云图Fig.6 Displacement of rectangular shell model

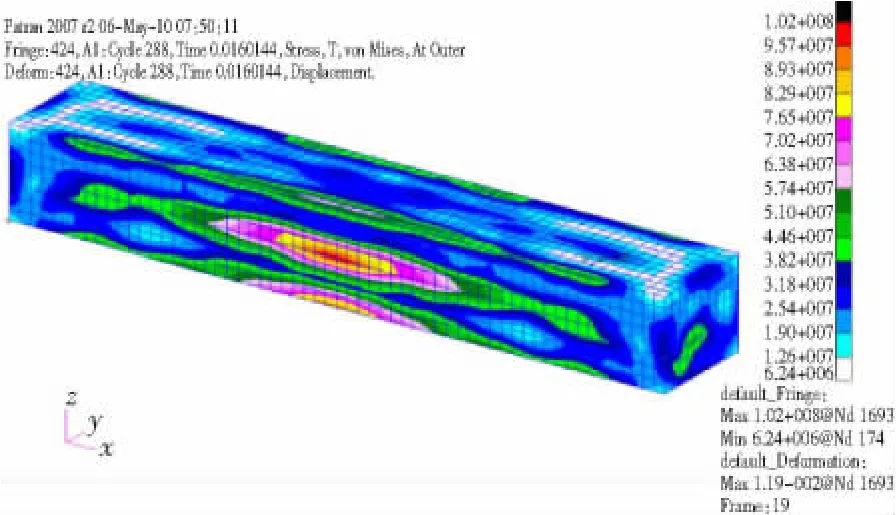
图7 模型应力云图Fig.7 Misses of rectangular shell model

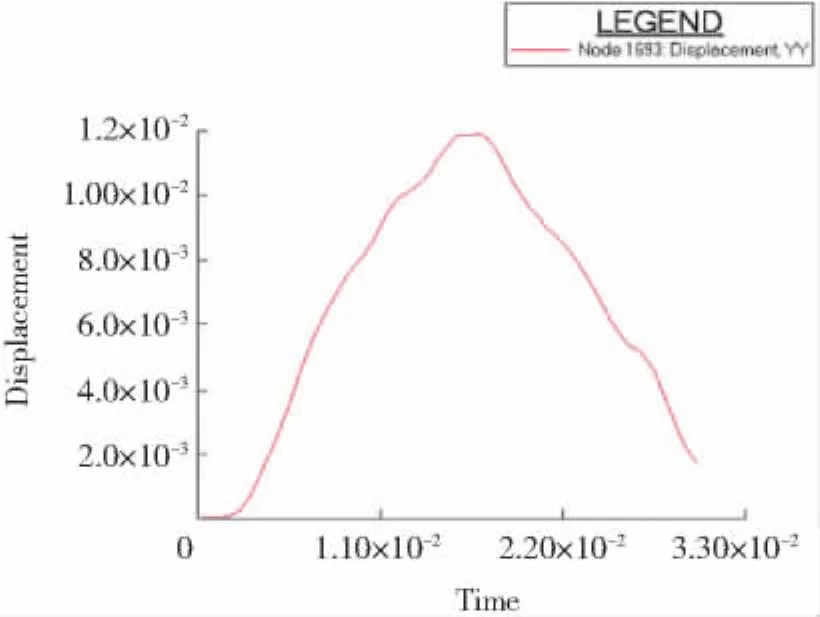
图8 A点水平方向位移曲线Fig.8 Horizontal displacement of node A

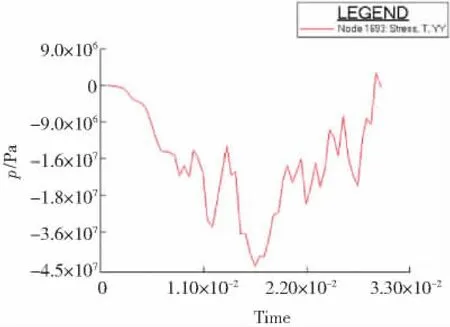
图9 A点水平方向应力曲线Fig.9 Horizontal stress of node A

2.3.2 静态等效分析

在MSC.PATRAN中建立相同的长方形壳体的有限元模型，在相应的面上分别施加3.1节所计算得到的静态等效载荷，图10－12所示为经过计算施加在前面上的等效冲击载荷。利用MSC.Nastran求解器进行分析，得到模型在静态载荷下的位移和应力响应，图10所示为模型正前面的等效静态载荷，图11所示为模型的位移云图，图12所示为模型的应力云图。

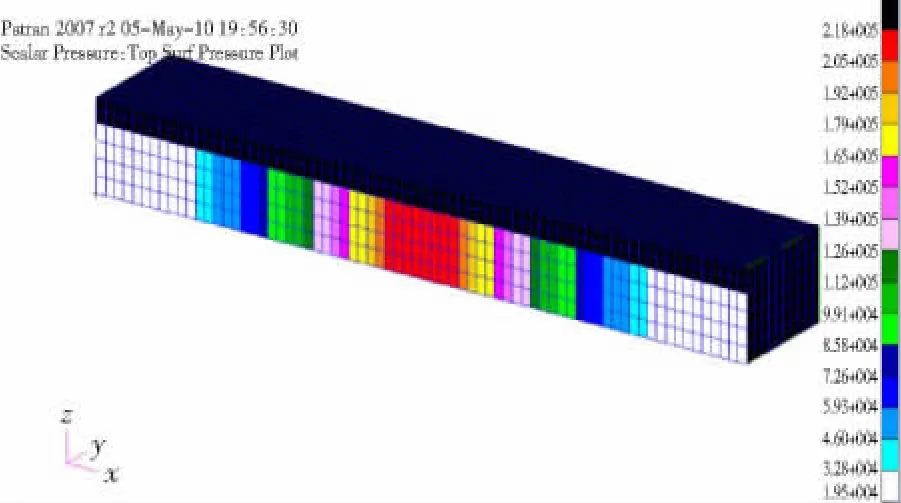
图10 前面的静态载荷Fig.10 Static load on front surface

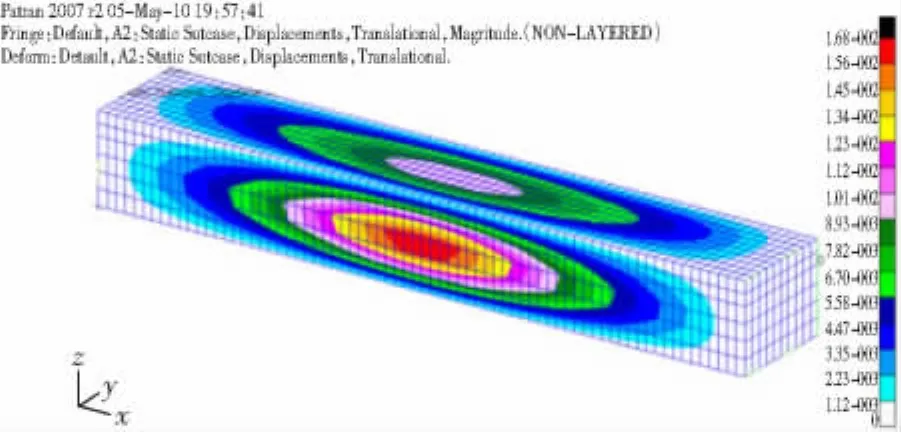
图11 模型位移云图Fig.11 Displacement of rectangular shell model

2.3.3 结果对比与分析

将上述动态和静态分析的结果进行对比，见表3。

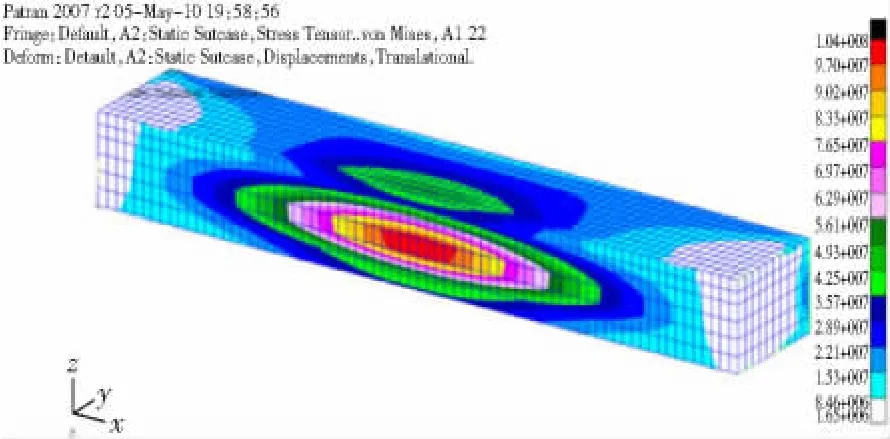
图12 模型应力云图Fig.12 Misses of rectangular shell model

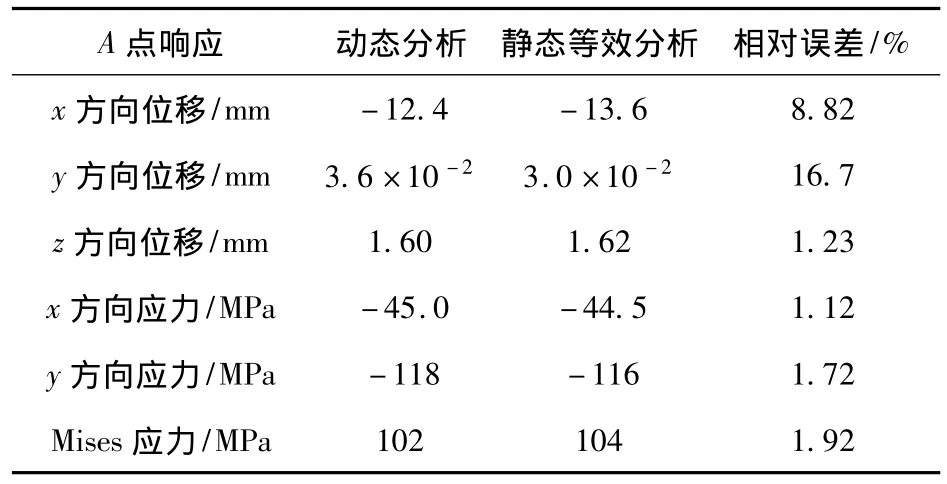
表3 分析结果对比Table 3 Contrast of two analyses results

由上表得出结论:两种分析结果的相对误差不大，水下爆炸动态冲击分析可以由上述静态等效分析的方法近似代替，可以简化计算。

3 结束语

根据能量原理、动量原理、达朗贝尔原理及附加质量原理，结合水下爆炸冲击理论，提出了静态等效分析方法，研究水下爆炸冲击下结构物的响应。以长方形壳体模型为算例，利用MATLAB软件进行编程，分别计算炸药爆炸后长方壳体吸收的能量、冲量，水平运动方向的附连水质量、初始速度及加速度等，得到长方形壳体湿面上受到的等效静载荷分布规律及载荷值。利用有限元分析软件MSC.Patran建立模型，将得到的等效静载荷施加在壳体湿面，在Nastran中进行静态分析，得到长方形壳体在静态等效载荷作用下的响应。响应结果与Dytran动态分析的结果近似相等，故该计算方法对于分析和计算水下爆炸载荷下结构物的响应是可行的。

［1］刘建湖.舰船非接触水下爆炸动力学的理论与应用［D］.无锡:中国船舶科学研究中心，2002.

［2］罗 超，谌 勇，张志谊.舰船水下非接触爆炸响应的数值模拟［J］.船海工程，2009，38(2):28－31.

［3］陈永念，谭家华.某型舰船水下爆炸冲击波载荷作用下结构动态响应数值仿真研究［J］.舰船科学技术，2007，29(4):105－109.

［4］陈永念，尹 群，胡海岩.水下爆炸冲击波载荷作用下舰船结构动态响应的数值模拟［J］.爆炸与冲击，2004，24(3):201－206.

［5］姚熊亮，侯 健，王玉红，等.水下爆炸冲击载荷作用时船舶冲击环境仿真［J］.中国造船，2003，44(1):71－74.

［6］姚熊亮，张阿漫，许维军，等.基于ABAQUS软件的舰船水下爆炸研究［J］.哈尔滨工程大学学报，2006，27(1):38－41.

［7］COLE R H.Underwater explosion［M］.［s.l.］:Princeton University Press，1948.

［8］金咸定，赵德有.船体振动学［M］.上海:上海交通大学出版社，2000:213－215.

［9］姚雄亮.船体振动［M］.哈尔滨:哈尔滨工程大学出版社，2004:148－150.

［10］白光辉.复合材料船艇结构选型及抗爆性能分析［D］.哈尔滨:哈尔滨工业大学，2010.

A static equivalence studies on underwater explosion load

BIAN Wenfeng1， MIAO Huiwen2， BAI Guanghui1， CHENG Jie1
(1.Department of Civil Engineering Harbin Institute of Technology(Weihai)264209，China;2.Zhongfu Xigang Ship Company Limited，Weihai 264209，China)

Underwater explosion exerts two effects on underground structure;one is the direct-pressure;the other is giving the underground structure both velocity and acceleration in such a way that both the structure itself and the added mass(added mass of entrained water)is given acceleration，namely the fact that underwater explosion causes a change in the kinetic energy and the momentum in both the structure and the added mass.It follows that the research into the response of structure acted on by underwater explosion poses a very complicated task involving considerable calculation.The analysis of the response of structure using an equivalent static analysis method could not only simplifies the structure analysis，but also produces an equivalent load value and application measure for structure design.This paper features methods designed for the analysis and calculation of equivalent static load of underwater explosion，based on the principle of energy and momentum as well as d’Alembert principle.The results verify the feasibility of this method.

underwater explosion;shock wave;static;equivalent;load

O389:U661

A

1671－0118(2012)04－0397－06

2012－04－21

国家高技术研究发展计划(863计划)项目(2007AA03A208)

边文凤(1963－)，女，黑龙江省肇东人，教授，博士生导师，研究方向:复合材料结构力学、船舶动力学，E-mail:bianwf@163.com。

(编辑 晁晓筠)