一致性方法的多仿生机器鱼编队对齐行为

台秀华

(兰州交通大学 机电工程学院，兰州 730070)

一致性方法的多仿生机器鱼编队对齐行为

台秀华

(兰州交通大学 机电工程学院，兰州 730070)

针对多仿生机器鱼编队中的对齐行为，利用一致性的方法，提出一种新颖的机器鱼编队控制方法。设定机器鱼群体的一致性协议，模拟一定的群体智能、群体行为，通过机器鱼之间的局部信息交流，群体方向最终达到一致。在机器鱼平台上分别对信息拓扑为无向图和有向图的情况进行了一致性实验验证。实验的初始条件是机器鱼个体的朝向和各自运动方向随机，实验的最后结果两种情况下机器鱼群体方向均达到了一致。实验结果表明，该方法是有效的，实现了编队的对齐行为。

机器鱼;一致性;多鱼编队;对齐行为

0 引言

仿生机器鱼在水中运输、水下搜救、军事侦察、海底资源勘探等环境极为复杂的水下有着广泛的应用前景。由于水下环境的复杂多变性、水下机器人自身特殊的推进方式，一般的协调控制方法很难直接应用到水下机器人的实体上。因此，多水下机器人的协调控制是机器人技术的研究热点、难点之一。

对于多水下机器人的编队协调控制，国内外进行了一些研究。日本Hokkaido大学的科研人员［1］，普林斯顿大学动力学控制系统实验室［2］，中科院自动化研究所 取得了一些研究经验和成果。北京大学智能控制实验室在此基础上做了进一步的研究，实现了多鱼队形控制，协作运输，合作顶球［4］。

一致性是指随着时间的演化，多智能体系统中的所有智能体，就某一协调变量的取值最终达成一致。而一致性协议是指智能体相互作用的规则，是每个智能体与其相邻的智能体之间的信息交换过程的描述。目前有些学者开始研究一致性机制在具体应用中的实际编队问题，比如说移动机器人的聚集和定位问题，无人驾驶飞行器的编队控制等。文献［5］将一致性理论应用到航天器编队飞行协同控制，并进行了仿真。

仿生机器鱼与陆地、空天机器人不同，不能倒退只能前行和转弯，而且水下环境复杂多变，鱼本身的游动会导致周围水体发生变化，影响周围的环境。一致性理论已经应用在多智能体系统的控制上，但是大部分是仿真实验验证算法的可行性和对系统的收敛性分析，而运用的领域也是陆地和空天领域。以目前的文献看，还没有将一致性理论应用在水中机器人中。笔者针对机器鱼编队的方向，初步实现一致性算法在水中多机器人系统中的应用——多仿生机器鱼的编队中的对齐行为，对多机器鱼编队有重要参考价值。

1 基于一致性的多机器鱼编队对齐行为

1.1 鱼的群体行为

自然界中的群体行为给研究复杂网络群体的协调控制一些很好的启示。在这个网络系统中每个个体直接或间接地与其他个体发生联系，并且系统的群体往往呈现出单个个体无法实现的复杂的行为。生物网络在自然界中很常见，包括鱼群、鸟群等群体，科学家们对生物群体行为的分析也做了一定的研究。Reynolds提出了著名的Boid模型，指出群体运动应该具有三个特征:(1)分离性，避免与相邻的个体发生碰撞;(2)聚合性，期望向邻近的个体的中心靠拢;(3)趋同性，朝向邻居个体的平均运动方向运动［6］。Vicsek等人提出了 Vicsek模型，其实是Boid模型的一种特殊情况，只满足Boid模型第三条规则。一个有趣的结果是:当智能体个体密度比较大且噪声比较小时，整个系统中的所有个体会出现行为上的一致，即运动方向会趋于一致，这就达到了多智能体系统的一致性［7］。

1.2 一致性协议

笔者就是在Vicsek模型基础上，运用一致性协议对机器鱼实体编队控制。

在一致性问题的研究中，图论是重要的分析工具。G=(V，E，A)为一个图，由边集合 E⊆V2，非空结点集合V={v1，v2，…，vn}，邻接矩阵 A构成。在有向图中，如果第i个节点有信息传递至第j个节点，则第i个节点有一条边指向第j个节点。在无向图中，节点对间的边没有方向。描述节点与边之间关系的矩阵称为邻接矩阵A。其中元素取值如下:如果第j个节点有一条边指向第i个节点，那么aij≥0，∀i≠j，其中对角线元素aii=0。普拉斯矩阵L是另一种描述图的拓扑结构的矩阵，它的取值式为

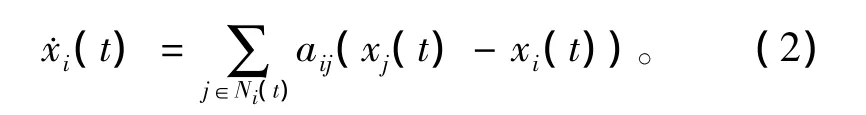
其中，Ni(t)表示t时刻所能传送信息给第i个智能体的邻居集，aij是一个非负实数，它表示第j个智能体传送信息给i个智能体信息的权值因子。若多智能体系统具有固定拓扑结构，则每个智能体的邻居集和权值因子从初始时刻开始保持不变。由式(2)可看出，每个智能体都朝着自己邻居的状态演化，由于这种局部的邻居间信息传递的机制，所有智能体的状态将逐渐趋于一致。

1.3 一致性方法的实现

将该多机器鱼系统视为在二维平面上的一群初始随机分布的智能体，与陆地等其他机器人不同，每个个体只能前游和转弯，不能倒退。每条机器鱼具有相同的运动速度和不同的方向，每条机器鱼只与其有信息关联的机器鱼进行信息交流。

1.3.1 机器鱼的运动方向

假设多智能体网络系统中有N个智能体，第i个智能体的状态 xi，i∈{1，2，…，n}。如果当 t→∞时，‖xi－ xj‖→0，∀i≠j，则称系统达到了一致。一致性协议描述了智能体之间的相互作用的规则，

如式(3)，其中˙φi(t)为机器鱼方向的控制仲裁器，aij表示第j个机器鱼传送信息给i个机器鱼信息的权值因子。依据˙φi(t)的仲裁，最终确定控制机器鱼到达所要期望的运动方向。在通信拓扑固定不变的情况下，利用固定拓扑连续时间一致性方法使四条机器鱼的方向达成一致。

1.3.2 信息拓扑图——无向图

当信息拓扑图为无向图时，系统收敛的状态将达到平均一致。如图1该信息图是无向图，机器鱼编队最终的一致性方向与每条鱼的初始状态有关，最终收敛于一致性平均值。信息图的拉普拉斯矩

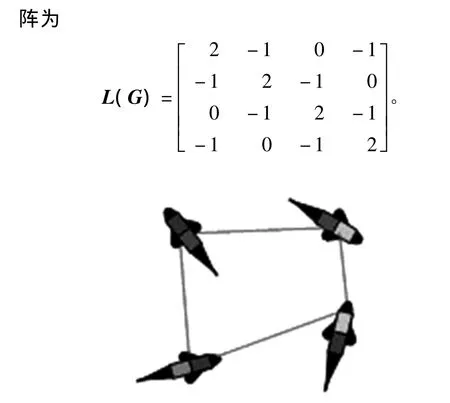
图1 信息交互图为无向图Fig.1 Undirected graph

1.3.3 信息拓扑图——有向图

当且仅当有向图中含有向生成树时，系统的状态能渐进收敛，达到一致。最终收敛的状态由初始状态、通信拓扑图、加权邻接矩阵共同决定。如图2信息拓扑图为有向图，包含有向生成树，有三个根节点。机器鱼编队最终的一致性方向与机器鱼1、2、3的初始状态有关，最终收敛于一致性加权平均值。信息图的加权拉普拉斯矩阵如下:

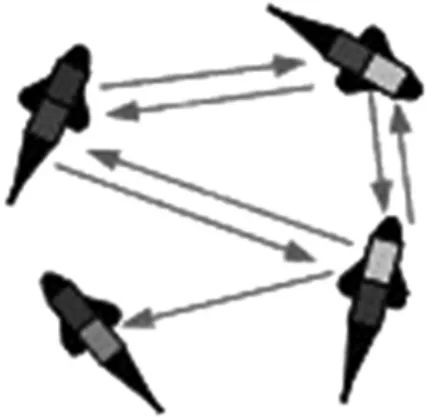
图2 信息交互图为有向图Fig.2 Directed graph

2 实验验证

利用多智能仿生机器鱼平台应用一致性协议分别对信息拓扑为无向图和有向图的情况进行一致性实验验证。

2.1 信息交互图——无向图

实验初始条件为四条鱼位置和朝向随机摆放，没有任何干预，完全靠机器鱼群个体的自助游动。四条机器鱼的初始状态如图3a。初始方向角见表1。

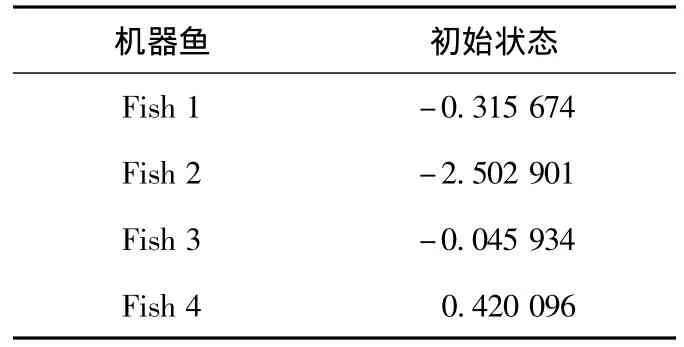
表1 机器鱼的初始状态一Table 1 Initial state of robotic fish

用到机器鱼实体中实验如图3。

图3 实验过程截图Fig.3 Experiment process screenshots

图3b、3c为机器鱼群根据一致性协议的规则开始不断的调整自己的运动方向。图3d所示在该时刻下基本达到了方向一致。

利用一致性算法得到仿真结果如图4。

图4 仿真实验Fig.4 Simulation experiment

由仿真实验的曲线，四条机器鱼组成的编队系统收敛，由于是无向图，最终收敛于平均状态－0.611 103 25，达到了一致。

图5为四条机器鱼实体方向的动态信息变化图。可以看出，四条机器鱼最终收敛，由于机器鱼本身在游动过程中鱼头会摆动，势必会影响到机器鱼本身的方向，故在理论一致性参考值的上下浮动。每条曲线分别代表 Fish1、Fish2、Fish3、Fish4各自的状态，其中Fish3的变化较大，且有一段时间状态持续为一固定值的现象。这是由于水中环境复杂性、水波、光照等原因，机器鱼识别不佳的缘故。最终实验结果表明，机器鱼群体信息交互图为无向图时，机器鱼实体也是根据一致性协议的规则不断的调整自己的运动方向，最终达到了方向一致性。

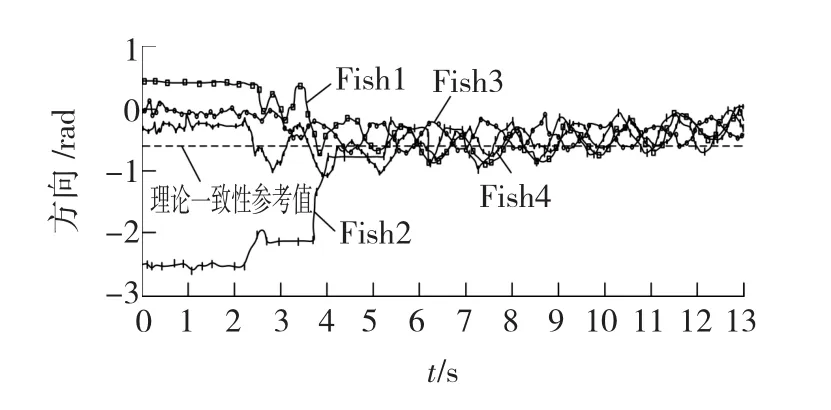
图5 机器鱼状态变化Fig.5 Robotic fish state changes

2.2 信息交互图——有向图

四条机器鱼的信息交互图为有向图时，如图2。实验初始条件还是四条鱼位置和朝向随机摆放。没有任何干预，完全靠机器鱼群个体的自助游动。四条机器鱼的初始状态如图6a。图6b、6c为机器鱼群根据一致性协议的规则开始不断的调整自己的运动方向，达到方向一致性的过程。图6d所示在该时刻下基本达到了方向一致。初始方向角见表2。

图6 实验二过程截图Fig.6 Experiment process screenshots

表2 机器鱼的初始状态二Table 2 Initial state of robotic fish

利用一致性算法得到仿真结果如图7。

图7 仿真实验Fig.7 Simulation experiment

由仿真实验的曲线，四条机器鱼组成的编队系统收敛，此信息图为有向图，包含有向生成树，有3个根节点，最终收敛于3个根节点的加权平均状态－0.737 461 75，达到了一致。

图8为四条机器鱼实体的方向的动态信息变化图。可以看出，与上一个实验一样，四条机器鱼最终收敛。

图8 机器鱼状态变化Fig.8 Robotic fish state changes

该信息交流拓扑图中Fish1、Fish2、Fish3为图的根节点，其中Fish2的权值最大为0.5，Fish1的权值为0.2，Fish3的权值为0.3，Fish4只受Fish3的影响。最终实验结果表明，当机器鱼的群体信息交互图为有向图并且还有有向生成树时，机器鱼实体也是根据一致性协议的规则不断的调整自己的运动方向，最终达到了方向一致性。

3 结论

本文使用群体智能的控制方法，将一致性的协议运用到多机器鱼编队中，通过机器鱼之间的相互作用、影响，方向最终达到一致，实现编队的对齐行为。由于目前的条件所限，并不能保证完全分布式控制，还需要通过多机器人协作控制系统中采集到的有关机器鱼的相关位姿信息，以分布式的控制思想运用一致性协议，最终使机器鱼群体达到方向一致性。文中的方法，不仅能为以后实现多条机器鱼以群体合作的方式完成个体本身不能完成的任务打下一定的基础，比如说多机器鱼组成一定的队形，进行排雷、布雷、水中探测、水中考古、水中搜索救援等复杂任务，而且可以用在异构的多智能体系统中，为异构的多智能体系统提供一种协调控制方法。

［1］LIJIMA D，YU W，YOKOI H.Obstacle avoidance learning for a multi-agent linked robot in the real world［C］//Proceedings of the 2001 IEEE International Conference on Robotics and Automation，New York:［s.n.］，2001:523 －528.

［2］LEONARD N E，FIORELLI E.Virtual Leaders，artificial Potentials and coordinated control of groups［C］//Proceedings of the 40th IEEE Conference on Decision and Control.［S.l.］:［s.

［3］喻俊志.多仿生机器鱼控制与协调研究［D］.北京:中国科学院自动化研究所，2003.

［4］SHAO J，WANG L，YU J.Development of an artificial fish-like robot and its application in cooperative transportation［J］.Control Engineering Practice，2008，16:569－584.

［5］毕 鹏，罗建军，张 博.一种基于一致性理论的航天器编队飞行协同控制方法［J］.宇航学报，2010，31(1):70－74.

［6］REYNOLDS C W.Flocks，herds，and schools:a distributed behavioralmodel［J］.Computer Graphics，1987，21(4):25 －34.

［7］VIESEK T，CZIROK A，BEN JACOB E，et al.Novel type of phase transition in a System of self-driven particles［J］.Phys Rev Lett，1995，75(6):1226 －1229.

Consensus-based method for formation alignment behavior of multi-robotic fish

TAI Xiuhua
(School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

This paper presents an attempt to address the alignment behavior of multi-robotic fish formation by proposing a novel controlling method for multi-robotic fish formation，depending on consensus protocol.The method consists of setting up the consensus of agreement of robotic fish group and simulating certain group intelligence and group activities，resulting in an eventual agreement in robotic fish group directions.The paper describes consensus experiments respectively on undirected graph and directed graph of information topology on the platform of robotic fish.The initial condition is such that the directions of each individual robotic fish and their respective movement are random，with the resultant consistency in the two circumstances robotic fish group directions，as shown by the final experiment.The method proves effective and thus enables the formation alignment behavior.

robotic fish;consensus;multi-robotic fish formation;alignment behavior

TP249

A

1671－0118(2012)01－0079－05

2012－01－01

台秀华(1987－)，男，山东省潍坊人，硕士，研究方向:机电一体化、智能控制，E-mail:taixiuhua@126.com。

(编辑 晁晓筠)