锚杆+微型桩复合土钉支护基坑稳定的可靠性
赵延林, 安伟光
(1.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.黑龙江科技学院 建筑工程学院,哈尔滨 150027)
锚杆+微型桩复合土钉支护基坑稳定的可靠性
赵延林1,2, 安伟光1
(1.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.黑龙江科技学院 建筑工程学院,哈尔滨 150027)
考虑预应力锚杆、微型桩与土钉的共同作用,应用边坡极限平衡理论与圆弧滑动条分法建立了预应力锚杆+微型桩复合土钉支护基坑内部整体稳定性分析的功能函数与最危险滑动面的计算模型。将土体的力学参数作为随机变量,推导了功能函数对各随机变量的偏导数。利用改进的一次二阶矩法计算了预应力锚杆+微型桩复合土钉支护基坑内部整体稳定的可靠性指标,并分析了土体力学参数的变异系数对可靠性指标的影响。
预应力锚杆;微型桩;复合土钉;可靠性
目前,预应力锚杆+微型桩复合土钉支护基坑的设计方法是基于边坡极限平衡理论与圆弧滑动条分法的定值分析方法[1-5]。由于土体力学参数的变异系数较大,这给定值分析结果带来不确定性[6-9]。因此,预应力锚杆+微型桩复合土钉支护基坑的设计,必须考虑土体力学参数的随机性,形成基于可靠性理论的复合土钉支护体系。
为此,笔者建立了预应力锚杆+微型桩复合土钉支护基坑内部整体稳定性分析的功能函数与最危险滑动面的计算模型,应用改进的一次二阶矩法计算了基坑内部整体稳定的可靠性指标,为形成基于可靠性理论的复合土钉支护体系的设计方法奠定了理论基础。
1 滑动面破坏模式
当微型桩植入土体深度较小时,最危险滑动面为“桩下弧”形式。此时,基坑的稳定性只与土钉的抗滑作用有关,而与微型桩的抗滑作用无关。当微桩有一定入土深度时,最危险滑动面为“桩底弧”形式。此时基坑的稳定性受微桩长度的影响,但计算中不涉及微型桩的抗滑作用。当微型桩入土深度较大时,最危险滑动面为“过桩弧”形式。此时基坑的稳定性不仅要考虑土钉的抗滑作用,还要考虑微型桩的抗滑作用;若桩身不破坏,桩底发生一定的位移,则形成“桩身双弧”滑动破坏面。
2 功能函数
不考虑土条间的相互作用力,应用边坡极限平衡理论与圆弧滑动条分法对预应力锚杆+微型桩复合土钉支护基坑内部整体稳定性进行分析,计算简图如图1所示。
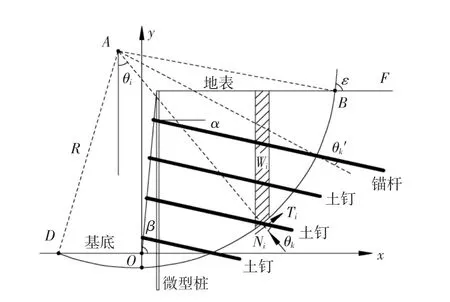
图1 基坑内部整体稳定性计算简图Fig.1 Calculation diagram of the inner global stability of foundation pit
预应力锚杆+微型桩复合土钉支护基坑内部整体稳定可靠性分析的功能函数为

预应力锚杆+微型桩复合土钉支护基坑内部整体稳
定分析的安全系数为

式中:Wi——第 i土条自重;
Qi——作用在第i土条上的地面超载;
cj、φj——第 i土条滑动面所在第 j土层的黏聚力与内摩擦角;
li——第i土条的滑动面长度;
θi——第i土条滑动面中点与竖直方向的夹角;
αmp——微型桩剪切面与水平方向的夹角;
Dd——土钉的锚固体直径;
Dm——锚杆的锚固体直径;
Dmp——微型桩的截面直径;
τj——土钉处于第j土层的界面黏结强度;
τmp——微型桩的抗剪强度;
θk——土钉与滑动面切线方向的夹角;
θ'k——锚杆与滑动面切线方向的夹角;
S1——土钉的水平间距;
S2——锚杆的水平间距;
S3——微型桩的水平间距。
3 最危险滑动面的计算方法
3.1 模型计算
以坡脚O为坐标原点,建立如图1所示直角坐标系。圆弧DCB为滑动面,点A(xA,yA)为圆弧滑动面的圆心。点B(xB,H)为滑动面与地表的交点,点C(0,yC)为滑动面与y轴的交点。由几何关系可知,圆弧滑动面的圆心坐标为
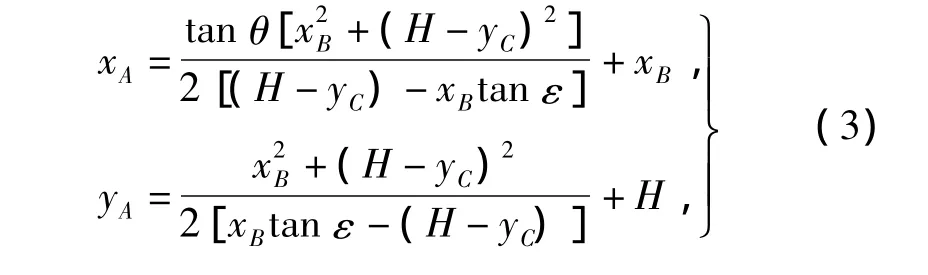
式中:ε——滑动面在B点处切线与水平方向的夹角;
H——基坑开挖深度。
由式(3)可知,当 xB、yC、ε均为已知值时,则圆弧滑动面的圆心A(xA,yA)、半径R唯一确定,圆弧相应的圆弧滑动面也唯一确定。因此,在给定yC的情况下,以点B处xB、ε两变量为基础,通过移动点B且改变点B处ε值,则可得到对应变化的圆弧方程,从而建立和实现滑移面搜索模型。
3.2 搜索计算
在图1中,使点B遍历线段BE上任意一点(xi,yi),搜索时变化该点处圆弧切线与水平方向夹角的取值,通过迭代变化yC取值,实现滑移面的搜索过程。αi为滑移面圆弧弦OO'与水平面的夹角,Δx、Δε、ΔyC分别为各变量的计算步长。
搜索过程中各变量变化的实现按式(4)进行:

安全系数最小值所对应的滑动面即为最危险滑动面。
4 可靠性计算方法
选取各土层的力学参数 cj、φj、τj作为随机变量,并假设所有随机变量均服从正态分布。则基坑内部整体稳定功能函数对各随机变量的偏导数为
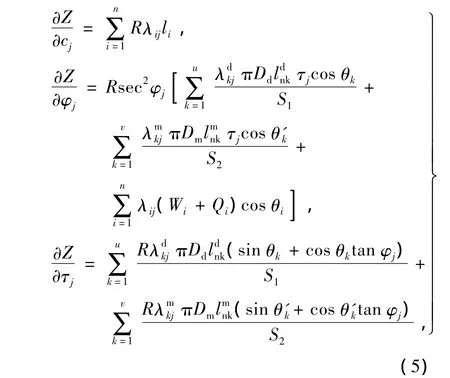
式中:λij、λdkj、λmkj为土层判别系数。λij若土条i底面在第j土层中其值取1,否则为0;λkj表示若第k层土钉处于第j土层中其值取1,否则为0;λmkj表示若第k层锚杆处于第j土层中其值取1,否则为0。
应用改进的一次二阶矩法计算预应力锚杆+微型桩复合土钉支护基坑内部整体稳定可靠性指标。为便于表达,将随机变量(c1,φ1,τ1,…,cm,φm,τm)记为(X1,X2,…,X3m),其中 m 为土层数。设 X*=(X*1,X*2,…,X*3m)为设计验算点,则基坑内部整体稳定可靠性指标的计算步骤如下:

式中:ρij——随机变量 Xi与 Xj的相关系数。(4)计算新的X*i值,

(6)将新的X*i与 βk作为初始值,重复(2)~(5)的步骤,直到前后两次求得的β值相差小于要求的精度为止,从而求得最终的可靠度指标β与相应的设计验算点X*。
将以上的计算过程编制计算程序,通过计算机实现迭代计算。
5 实例分析
北京市某基坑工程,开挖深度为13.5 m,采用预应力锚杆+微型桩复合土钉支护方案,坡角为86°,如图2所示。微型桩桩径108 mm,间距1.5 m,桩长14.5 m;设置8排土钉,采用螺纹钢φ20 mm,倾角10°,土钉垂直间距为 1.4 m,水平间距均为1.4 m;其中第二、四排为预应力锚杆,采用2根7φ5 mm钢绞线,孔径为100 mm,倾角为15°;土钉墙面层采用钢筋网片,规格为 φ6 mm@200 mm×
,喷射细石混凝土面层厚度为80 mm,强度等级为C20。

图2 基坑支护I-I剖面Fig.2 I-I section of foundation pit
场地土层分布及其力学参数的数学统计特征如表1 所示。其中,μc、μφ、μτ分别为 c、φ、τ的均值,δc、δφ、δτ分别为 c、φ、τ的变异系数。
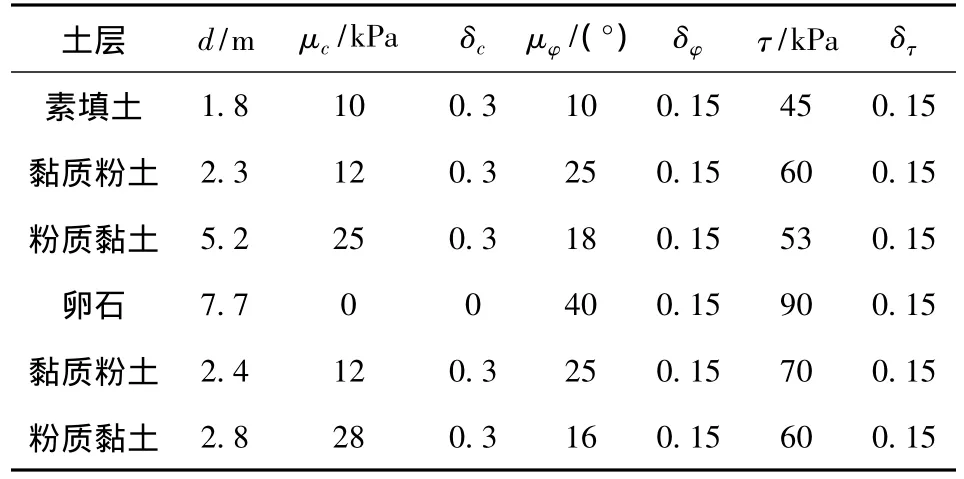
表1 土层力学参数的数学统计特征值Table 1 Statistical characteristics of mechanical parameters of soil layers
经计算可知,基坑的内部整体稳定可靠性指标为β=3.35,相应的最危险滑动面形式为“桩下弧”。
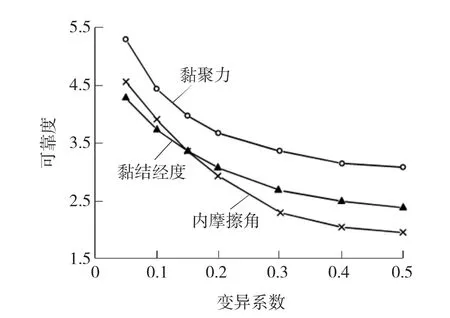
图3 可靠度与变异系数的关系Fig.3 Relation of reliability index and coefficient of variability
图3所示为第三层土(黏性土)力学参数c、φ、τ的变异系数对可靠度β的影响情况。由图可知,β值受c、φ、τ变异系数的影响较大,并随变异系数的增大而减小。其中,φ的变异系数对β的影响最大,c、τ的变异系数对β的影响最小。随着变异系数的增大,其对β的影响逐渐减小。
6 结论
基于边坡极限平衡理论、圆弧滑动条分法与改进的一次二阶矩法,提出了一种预应力锚杆+微型桩复合土钉支护基坑内部整体稳定可靠性的计算方法。结合实际工程,分析了土体力学参数的变异系数对基坑内部整体稳定可靠性指标的影响。分析表明:基坑内部整体稳定可靠性指标β值受c、φ、τ变异系数的影响较大,并随变异系数的增大而减小。其中,φ的变异系数对β的影响最大,c、τ的变异系数对β的影响最小。随着变异系数的增大,其对β的影响逐渐减小。
[1]屠毓敏,鲁美霞.复合土钉墙中垂直支护桩临界桩长的研究[J].岩土工程学报,2006,28(11):2023-2026.
[2]聂振军,李海深.微型桩+土钉复合型支护内部稳定性的探讨[J].土工基础,2009,23(3):47-49.
[3]李象范,尹 骥,管 飞.松软地层中基坑工程的复合型土钉支护[J].岩石力学与工程学报,2005,24(21):3876-3881.
[4]屠毓敏.软弱基坑中土钉墙整体稳定性分析应注意的问题[J].岩土工程学报,2008,30(4):591-594.
[5]李连祥,李术才,李春鹏.一般复合土钉墙结构整体稳定性研究[C]//第十届全国岩石力学与工程学术大会论文集.北京:中国电力出版社,2008:450-454.
[6]谭晓慧,王建国,冯敏杰,等.土钉支护结构可靠度分析的电子表格法[J].岩土力学,2009,30(11):3447-3452.
[7] YUAN JIANXIN,YANG YUWEN,LESLIE GEORGE THAM.New approach to limit equilibrium and reliability anlysis of soil nailed walls[J].International Journal of Geomechanics,2003,3(2):145 -151.
[8]罗晓辉,李再光,何立红.基于可靠性分析的基坑土钉支护稳定性[J].岩土工程学报,2006,28(4):480-484.
[9]吴忠诚,杨志银,罗小满,等.疏排桩锚—土钉墙组合支护结构稳定性分析[J].岩石力学与工程学报,2006,25(z2):3607-3613.
Reliability of stability of foundation pit supported by pre-stressed soil anchor+micro-pile composite soil nailing
ZHAO Yanlin1,2, AN Weiguang1
(1.College of Aerospace & Civil Engineering,Harbin Engineering University,Harbin 150001,China;2.College of Civil Engineering,Heilongjiang Institute of Science& Technology,Harbin 150027,China)
Given the co-action of pre-stressed soil anchor,micro-pile,and soil nailing,this paper begins with the application of the slope limit equilibrium theory and the circular sliding slice method to the development of the performance function and the calculation model of sliding surface for the inner global stability of foundation pit supported by the pre-stressed soil anchor+micro-pile composite soil nailing.The paper proceeds with the deduction of the partial derivatives of the performance function to all random variables with the shear strength indexes of soil as random variables,and the use of the improved first order second moment method to the calculation of the reliability index of inner global stability of foundation pit supported by the pre-stressed soil anchor+micro-pile composite soil nailing,and ends with an analysis of the effects of coefficients of variability of the random variables on reliability index.
pre-stressed soil anchor;micro-pile;composite soil nailing;reliability
TU472
A
2011-12-14
赵延林(1971-),男,山东省莱阳人,副教授,博士研究生,研究方向:深基坑工程,E-mail:zhaoyanlin1971@sina.com。
1671-0118(2012)01-0060-04
(编辑 晁晓筠)

