正交实验法薄壁压杆截面稳定性的优化

阎龙海， 金冬梅

(黑龙江科技学院 理学院，哈尔滨 150027)

正交实验法薄壁压杆截面稳定性的优化

阎龙海， 金冬梅

(黑龙江科技学院 理学院，哈尔滨 150027)

针对薄壁结构在工程中失稳破坏的问题，采用ANSYS软件对薄壁压杆双重非线性稳定进行分析，以薄壁压杆工字形截面尺寸为稳定极限载荷的影响因子，通过正交实验方法设计实验，得到了各个因子影响的显著性。翼缘宽度对稳定极限载荷的影响最大，翼缘厚度次之。最后依据多元线性回归原理建立了薄壁压杆稳定数学模型并对截面进行了优化设计，稳定极限载荷提高了30%。

薄壁压杆;稳定极限载荷;正交试验设计;多元线性回归

0 引言

目前，一般结构优化设计方法最后都归结到目标函数的极值上。其实要达到优化目的不必仅仅停留在目标函数的极值上，或者不完全归结为求极值问题。也就是说，可以把目标函数当作判断的一个根据，分析影响结构设计的变量，在目标函数邻近的范围内求出各种变量的变化情况及其对目标函数影响的大小，为设计者提供参数以达到优化的目的。薄壁结构具有自身重量轻、弯曲刚度高和承载能力强等特点，在工程领域应用广泛。在荷载作用下薄壁结构破坏的主要形式是屈曲失稳［1－4］，而影响薄壁压杆失稳的最主要因素是的截面尺寸。以工程中的工字型截面为例，影响其稳定的截面变量有腹板的厚度和高度，以及翼缘的宽度和高度。直接建立极限载荷和截面尺寸之间的数学表达式相当困难。笔者采用正交实验设计方法［5－6］建立极限载荷和截面尺寸间的数学表达式，进而实现截面稳定性的优化。

1 数值模拟

求解结构稳定问题的实质是求结构在给定荷载作用下的一种临界状态，确定临界荷载和相应的屈曲形态。较简单的结构可以用弹性力学的方法求得解析解，对于复杂结构用解析方法求解比较困难，而用数值方法往往可以得到较好的结果。文中采用有限元分析软件ANSYS对薄壁压杆进行双重非线性稳定分析。

1.1 有限元模型

1.1.1 单元选取

为分析工程结构中薄壁压杆具有几何和材料双重非线性的稳定问题，选取BEAM189单元作为基本单元类型。

图1BEAM189单元Fig.1 BEAM189 element

1.1.2 材料和截面特性选择

薄壁压杆的弹性模量E206 GPa，泊松比0.3，材料的屈服极限200 MPa。材料本构关系模型为理想弹塑性模型(图2)，运用Von Mises屈服准则，且不考虑强化的影响，在ANSYS程序中为BK模型。在ANSYS软件求解过程中开启相关几何非线性选项。工字型截面直接在ANSYS中以命令形式生成。

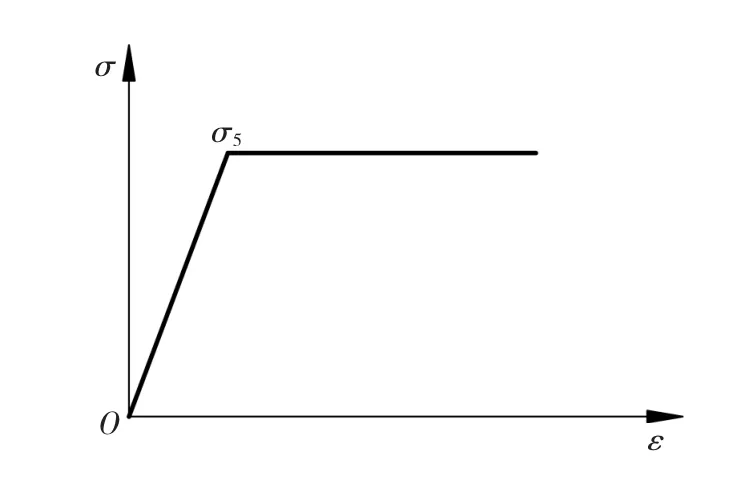
图2 材料本构关系Fig.2 Constitutive relations of materials

1.1.3 有限元模型的建立

薄壁压杆长度为2.5 m，直接建模法建立的薄壁压杆有限元模型如图3所示。

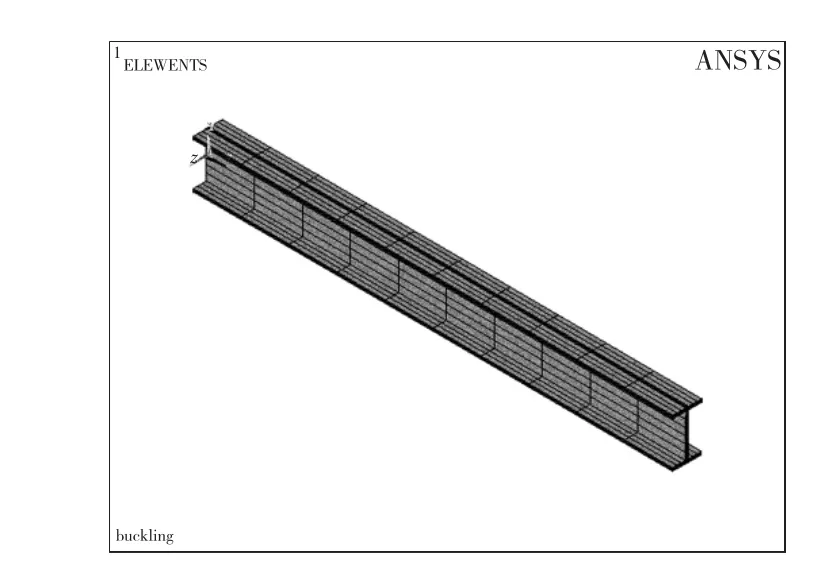
图3 薄壁压杆有限元模型Fig.3 Finite element model of thin-walled compressive bar

1.1.4 约束条件

薄壁压杆采用一端固定一端自由的边界条件。

1.2 稳定分析

进行ANSYS求解，首先得到线性稳定分析结果。薄壁压杆线性稳定分析的屈曲载荷为690 kN。线性稳定分析主要用于预测理想结构的理论屈曲强度。从工程角度分析，结构的大变形、初始缺陷以及材料非线性使得多数结构都不是在理想的弹性屈曲强度处发生屈曲，但线性稳定分析可以为非线性稳定分析提供以下依据。

进入时间历程后处理器，定义变量自由端节点的y方向位移，定义变量固定端节点的约束反力，绘制结构中最大位移点载荷位移曲线(图4)。通过图4可以看出薄壁压杆的稳定极限载荷为508 kN，比线性稳定分析得出的极限屈曲载荷减少了26.4%。

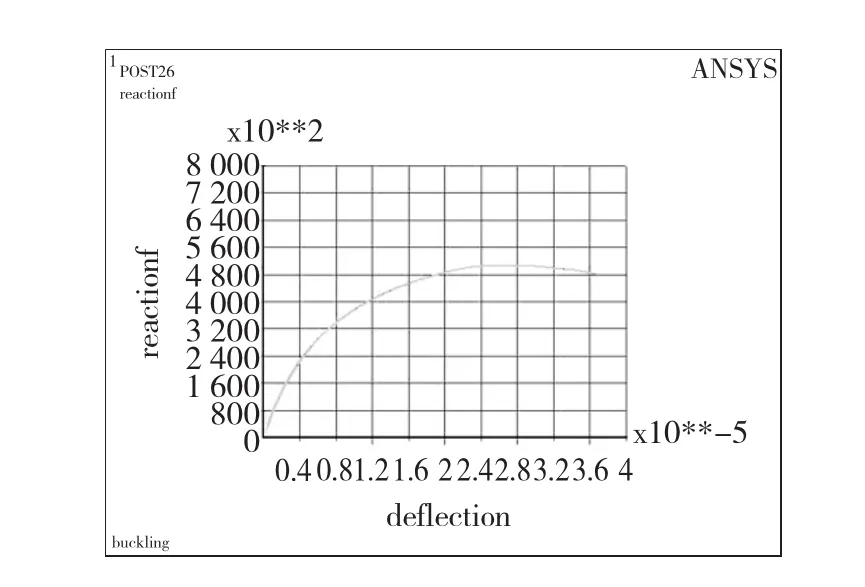
图4 最大位移点载荷－位移曲线Fig.4 Load－deflection curve of maximum deflection point

2 实验设计与结果分析

为确定工字型截面各尺寸对薄壁压杆稳定极限载荷的影响程度，采用正交实验设计法设计实验方案。以结构稳定极限载荷为评价指标，选取工字形截面的翼缘宽度、翼缘厚度、腹板高度和腹板厚度四个尺寸为实验因素，每个因素选定三个水平。考虑到本结构的现实条件，不考虑截面各因素之间存在的交互影响，选取了四个因素三个水平的正交表L9(34)，实验方案见表1。

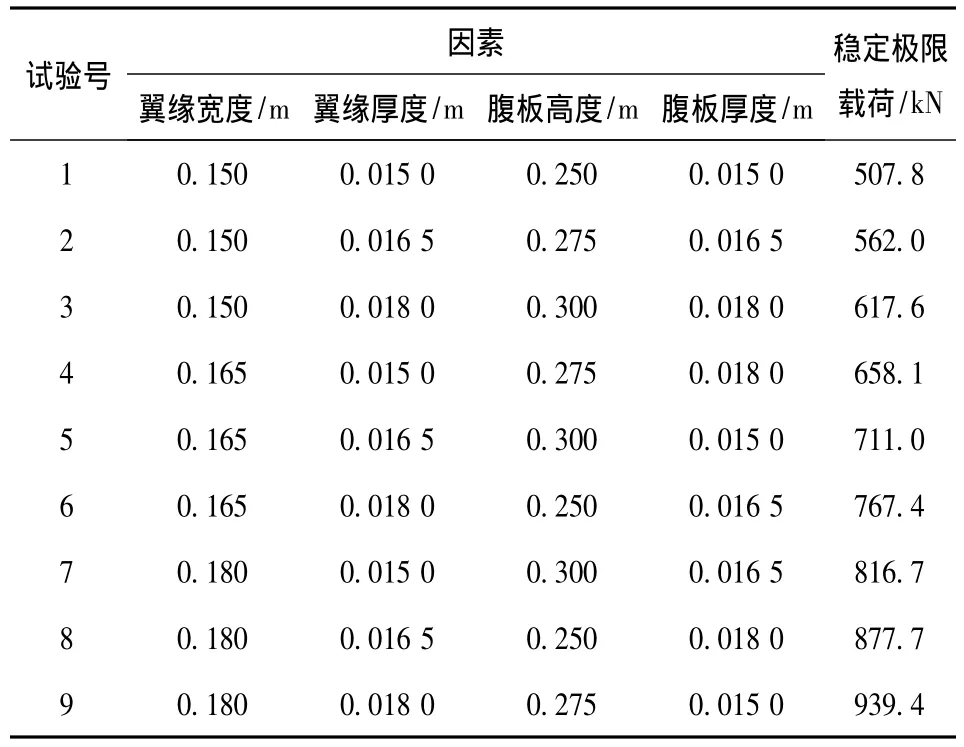
表1 正交实验数据及结果Table 1 Orthogonal experimental data and result

通过直观分析方法，计算Ki、ki和R，得到正交实验设计影响因素直观分析表(表2)，并作出评价指标与实验因素关系趋势图(图5)。

表2 影响因素的直观分析Table 2 Visual analysis of influencing factor mm

图5 评价指标与实验因素影响趋势Fig.5 Tendency chart of influence of evaluating indicator and experimental factor

表2和图5显示，对稳定极限载荷而言，翼缘宽度的极差最大，翼缘宽度对稳定极限载荷的影响最大，翼缘厚度次之;腹板高度和腹板厚度的极差较小，接近水平直线，对稳定极限载荷的影响较小，可以把他们当作误差项处理。稳定极限载荷与显著因子翼缘宽度和翼缘厚度之间存在比较明显的线性关系。

3 优化分析

根据实验结果分析，采用多元线性回归原理建立优化模型。设自变量x1为截面的翼缘宽度，x2为截面的翼缘厚度，因变量y为薄壁压杆的稳定极限载荷，建立模型:

式中，β0为常数项，β1、β2为 y对 x1和 x2的偏回归系数，分别反映了自变量x1和x2对因变量y的影响程度。

将实验数据代入，求出二元线性回归方程的回归系数 β0、β1和 β2，得到理论回归方程

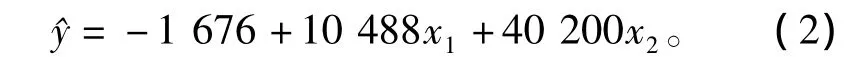
对方程(2)进行统计检验，列出多元线性回归方差分析表(表3)

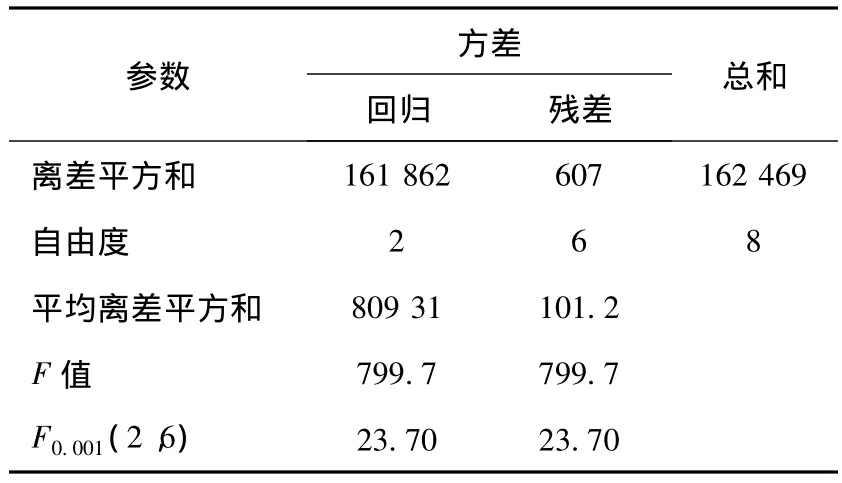
表3 多元线性回归方差分析Table 3 Analysis of variance table of multiple linear regression

用统计量F=MSR/MSe～Fα(m，n－m －1)来衡量回归效果。从表3可以看出，当α=0.001时，F≥Fcr，效果很显著。根据公式，复相关系数 R为0.998。当R接近1时，相对误差量接近零，说明线性效果好，回归方程有很好的可靠性，在设计中有参考价值。

薄壁压杆长度2.5 m，原工字形截面原翼缘宽度与厚度、腹板高度与厚度分别为0.15、0.015、0.25和0.015 m，双重非线性稳定极限载荷为508 kN。增大工字形截面尺寸可提高薄壁压杆的稳定极限载荷，如截面各方向尺寸按等比例增加3%，增加的总面积为0.000 365 m2，经仿真计算稳定极限载荷为562 kN。优化设计就是在保持截面面积相等的条件下，得到最大的稳定极限载荷。通过正交试验设计方法，显著因子为翼缘宽度和翼缘厚度，保持截面腹板部分面积不变，增加翼缘部分的面积，翼缘部分的面积变为新的翼缘宽度x1和翼缘厚度x2的乘积，且满足x1·x2=0.002 615 m2。将相关数据代入线性回归方程式(2)有

在x1=0.17 436 m时，取得极大值为730 kN，此时x2=0.015 m，在面积相等的情况下，与562 kN相比提高承载30%。

4 结论

(1)利用有限元软件ANSYS建立薄壁压杆稳定有限元模型，通过数值仿真对薄壁压杆进行了双重非线性稳定分析，并得出稳定极限载荷。

(2)以薄壁压杆工字形截面的翼缘宽度、厚度、腹板高度和厚度作为评价指标稳定极限载荷的影响因子，采用正交实验方法，通过数值仿真得到实验结果，径直观分析方法得到了各个因子影响的显著性。

(3)建立了薄壁压杆截面优化设计数学模型，利用线性回归的控制功能实现优化设计。

(4)该方法为复杂结构的设计及优化设计提供了参考。

［1］ 陈 骥.钢结构稳定理论与设计［M］.3版.北京:科学出版社，2006.

［2］MEEK J L，XUE QIANG.A study on the instability problem for 3D frame［J］.Computer Methods Appl Mech Engrg，1998，158:235－254.

［3］KARIM ABEDI，PARKE G A R.Dynamic propagation of local instability in single-layer braced domes［C］//TIEN T LAW.Proceedings of Asia-Pacific Conference on Shell and Spatial Structures T Laneds.Beijing:［s.n.］，1996:556 －563.

［4］ 郝文化.ANSYS土木工程应用实例［M］.北京:中国水利水电出版社，2005.

［5］YANG DONGMEI，KOGISO N，MUROTSU.Structural optimization based on the experimental design method［J］.Chinese Journal of Computational Mechanics，2001，18(20):173 －178.

［6］YANG DONGMEI，KOGISO N，MUROTSU Y.Global optimal design based on the experimental design method［C］//Proceedings of the First China-Japan-Korea Joint Symposium on Optimization Structural and Mechanical Systems.Xian:［s.n.］，1999:516－523.

Section stability optimum of thin-walled compressive bar on orthogonal experimental method

YAN Longhai，JIN Dongmei
(College of Sciences，Heilongjiang Institute of Science＆ Technology，Harbin 150027，China)

Aimed at removing instability and failure associated with thin-walled compressive bar in engineering，this paper features appreciable impact of each factors，based on orthogonal experimental method and by analyzing the bi-nonlinear stability of thin-walled compressive bar，selecting sectional dimension of I-shaped cross-section as factors of ultimate load of thin-walled compressive bar，and performing the orthogonal experimental design.Flange width exerts the greatest effect on stability ultimate loads，followed by flange thickness.The paper ends with the development of mathematic model of thin-walled compressive bar by multiple linear regression theory and design of section optimum，thus giving a 30%.increase in section and ultimate load.

thin-walled compressive bar;stability ultimate loads;orthogonal experimental design;multiple linear regression

TU323

A

1671－0118(2012)01－0064－04

2012－01－09

阎龙海(1979－)，男，黑龙江省七台河人，讲师，硕士，研究方向:工程结构仿真、优化设计，E-mail:ylhqth2004@163.com。

(编辑 晁晓筠)