新型旋流沉砂池砂粒去除效果的数值模拟

邵超，叶勇，汪家权* ，张辉，王淦，侯红勋，王晶

1.合肥工业大学资源与环境工程学院，安徽 合肥 230009

2.安徽国祯环保节能科技股份有限公司，安徽 合肥 230088

沉砂池作为污水处理中必不可少的预处理设施，主要是去除含砂废水中一定直径的砂粒，减少砂粒对机械设备造成的过度磨损，以保证后续处理单元能够正常运行［1-2］。常用的沉砂池有平流式沉砂池、曝气沉砂池、旋流沉砂池等［3］。近年来，旋流沉砂池得到越来越多的应用，主要由于该类沉砂池具有占地省、除砂效率高、操作环境好、设备运行可靠等优点［2，4-6］。目前具有代表性的旋流沉砂池主要是美国Smith＆Loveless公司开发的比氏(Pista)沉砂池和英国Jones＆Attwood公司开发的钟式(Jeta)沉砂池［3］。

目前针对旋流沉砂池的数值模拟国内鲜有研究，Wang等［7］利用Star-CD商业软件对某污水处理厂的旋流沉砂池进行数值模拟，得到了相应的流场分布及不同砂粒运行轨迹，并采用实际的砂粒粒径计算出相应的砂粒去除率;栾闯［8］采用Eulerian-Eulerian模型和Eulerian-Lagrangian模型模拟分析了瀑布沟旋流沉砂池原有工况下的流场情况和砂石颗粒分布，并由不同转速和不同桨叶位置的数值模拟结果得出最佳工况的桨叶转速为105 r/min，桨叶位置为 592 mm;李涛［9］采用 Eulerian-Eulerian模型和Eulerian-Lagrangian模型模拟分析了旋流沉砂池内搅拌桨叶片数量、叶片角度和水力停留时间(HRT)对砂石颗粒去除效果的影响，认为当叶片数量为4片，叶片角度为45°，HRT为90 s时旋流沉砂池的效果最佳。

笔者从流场和颗粒运动等方面对旋流沉砂池的机理、搅拌桨运动以及进水流速变化对砂粒去除效果的影响进行研究，以期为旋流沉砂池的设计和改进提供理论参考。

1 搅拌器

根据搅拌器的运动方向与桨叶表面的角度可以将搅拌桨叶形状分为平叶、折叶和螺旋面叶［10］三类。实验采用的搅拌桨叶是折叶型，折叶由于桨面与运动方向成一定倾斜角(θ)，所以在桨叶运动时，除有水平环流外，还有轴向分流，在桨叶转速增大时，还有逐渐增大的径向流。根据桨叶排液方向将典型的桨叶分成径流型和轴流型(图1)，折叶桨居于二者之间［10-11］。其中径流型搅拌器在一定转速下旋转时，自桨叶处排出高速流体，该高速流体同时吸引挟带着周围的液体，使周围的静止流或低速流卷入到高速流中，径流型搅拌器浆叶产生一种“蝴蝶”型流态，搅拌桨从池顶部和底部吸引挟带物质，沿着搅拌桨两侧径向排出;轴流型搅拌器自桨叶排出的高速流是轴向的，其对周围的低速流同样具有吸引挟带作用，但不同于径流型的流态，轴流型是从顶部吸引挟带物质，然后从池底部排出［10-11］。

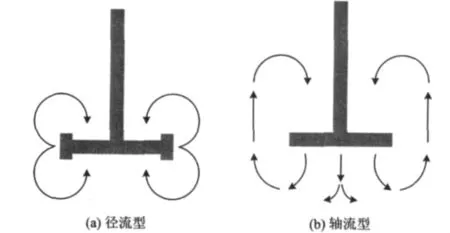
图1 径流型与轴流型搅拌器Fig.1 Runoff-type and axial-type agitator

2 计算模型的建立

2.1 数学模型

2.1.1 湍流模型

由于旋流沉砂池的流场大多由旋流态占主导，周国忠等［12］对搅拌槽内三维流动场数值模拟的研究表明，相对于标准k-ε模型，RNG k-ε湍流模型在耗散率方程中通过系数C1*引入描述流场畸变效应的附加源项后，在一定程度上改善了对桨叶附近各向异性湍流的预报能力，对速度场的预报比k-ε模型更加准确。因此，可以采用RNG k-ε湍流模型，该模型可以更好地处理高应变率及流线弯曲程度较大的流动，主要针对充分发展的湍流流动，即高Re数的湍流计算模型［13-14］;而对于近壁区的流动采用壁面加强函数法求解。具体的k和ε方程如下［14-16］:

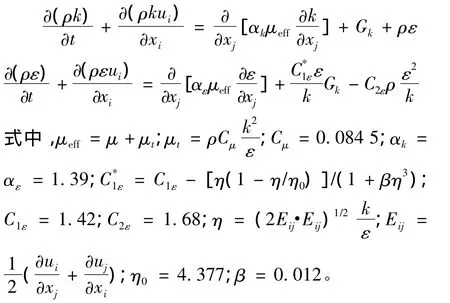
2.1.2 离散相模型与颗粒尺寸分布

实验使用的离散相颗粒为砂粒，假设颗粒为均匀球体，其体积分数小于12%，因此采用离散相模型(DPM)，可以忽略颗粒与颗粒间的相互作用、颗粒体积分数对连续相的影响［17］。假设离散相在流场中的质量及动量载荷率很低，在该情况下，连续相流场基本不受离散相的影响，可以忽略颗粒相对连续相的影响［18］。

在CFD中通过积分拉氏坐标系下的颗粒作用力微分方程求解离散相颗粒的轨道［17］。颗粒的作用力微分方程在笛卡尔坐标系下的形式(x方向)为:

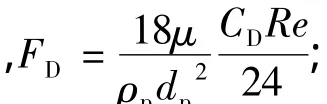
对颗粒尺寸进行 Rosin-Rammler分布拟合［17，19］，其中 Rosin-Rammler分布函数通常写成:

式中，Y为小于直径 D的颗粒的质量分数;¯d为Rosin-Rammler直径;n为Rosin-Rammler指数。

2.2 几何模型

实验模型主要由进水口、沉砂池池体、出水口、集砂斗和搅拌桨等组成，如图2所示。其中搅拌桨的旋转方向为顺时针。

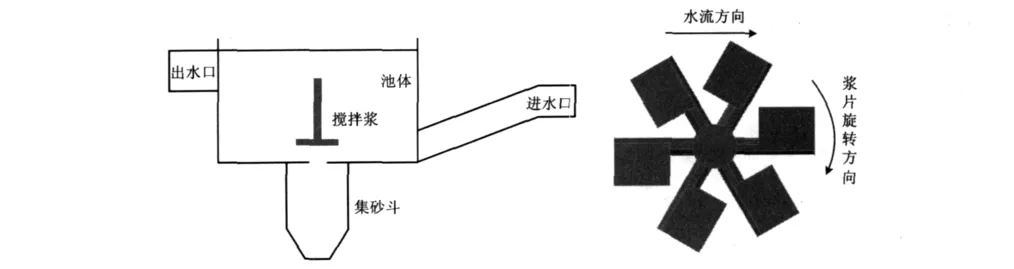
图2 新型旋流沉砂池和搅拌桨示意Fig.2 Schematic diagram of the new rotational flow grit chamber and the agitator

2.3 边界条件与网格划分

在不影响求解计算结果的条件下，对旋流沉砂池小试模型进行简化，忽略池体的壁厚，只考虑与流动区域直接接触的内部区域。采用三维模型，对旋流沉砂池小试模型进行建模和网格划分，设置边壁和搅拌桨叶片为固体壁面，固体壁面上采用无滑移边界条件，即u=v=w=0，近壁流动区采用壁面函数法处理。假定系统处于稳态过程，搅拌过程采用多重参考系模型(MRF)，砂粒的运动过程采用离散相模型(DPM)。

网格分为结构网格和非结构网格两大类［13］。在旋流沉砂池中，由于模型结构比较复杂，对其进行三维流场数值计算，网格质量的优劣直接影响到计算精度和收敛性。因此，对于旋流沉砂池模型的网格划分采用分块处理［18］，如图3所示。

图3 沉砂池模型网格划分示意Fig.3 Schematic diagram of grit chamber model meshing

3 流场模拟

3.1 压力场与速度场

3.1.1 压力场

沉砂池内的压强分布如图4所示。由图4可以看出，在旋流沉砂池底部附近，压强由池壁向池心递减(池壁附近的压强明显大于池体中部的压强):砂粒在由入口进入池体内运动的过程中，压强逐渐降低(在池壁与搅拌桨之间的区域)，如图4红色方框区域所示，该处的压强变化较为明显，这种压强差促使砂粒不断向池中心附近移动;另外，在搅拌桨处压强较大，而在池心靠近砂斗口附近压强处于较低值，该区域所形成的压强差可以进一步使聚集在水平池底的砂粒(靠近搅拌桨附近)向池心运动，并落入砂斗中。

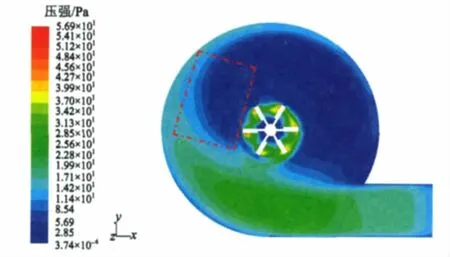
图4 搅拌桨倾角60°下压强分布Fig.4 Under impeller angle 60°pressure distribution

从砂粒运行轨迹(图5)看，砂粒主要在红色圆框区域附近向池心移动，并落入砂斗内。从压强角度看，砂粒在沉砂池内的运动及沉降主要依赖于压强变化，且某区域压强差越大，砂粒的运动越明显。

图5 砂粒运行轨迹Fig.5 The trajectories of sand

3.1.2 速度场

折叶搅拌桨在旋转的过程中自桨叶排出的高速流是轴向的，且对周围的低速流具有吸引挟带的作用［10］，由此在池体内形成轴向环流流态，沉砂池内部速度矢量如图6所示。

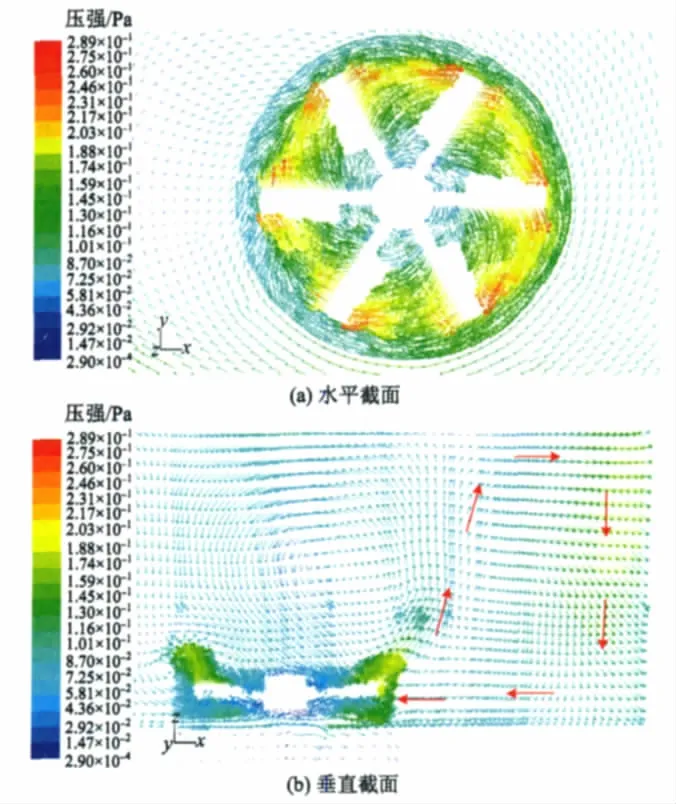
图6 沉砂池内部速度矢量Fig.6 The velocity vector in the grit chamber

图6(a)为沉砂池内部水平截面速度矢量，液面形成水平环流流场，有助于池体内的砂粒在离心力的作用下向池壁附近移动;图6(b)为沉砂池内部垂直截面速度矢量，在搅拌桨附近存在明显的轴向流流场，该流场不仅有助于砂粒较快沉降于池底，而且也使得水平池底的砂粒在该流场作用下向池心移动并落入砂斗内。因此，在水平环流和垂直环流的共同作用下，水流在沉砂池中以螺旋状前进，砂粒则在该流场的作用下，不断向池心汇集并落入砂斗内［5-6］。

3.2 搅拌桨静止和非静止(一定的进水流速)时池体内流场变化

当z=0.065 mm时，搅拌桨静止和非静止时的压强分布如图7所示。由图7可以看出，搅拌桨在非静止时的最大压强明显大于静止时，且最大压强的分布区域也不同，静止时处于入流口附近，而非静止时处于搅拌桨附近，这说明搅拌桨的运动会改变池体内压强值，并对池体内的压强分布产生一定的影响;但静止与非静止两种情况在入流口附近的压强相似，并没有因搅拌桨的运动而发生较大差异。另外，从图7的红色方框区域可以看出，静止时在池体中部尤其是搅拌桨附近有很大区域压强值处于最低值且不存在压强变化，这使得砂粒易于在该处堆积;而非静止时，压强在由池壁到池心存在明显的变化，形成的压强差将有助于砂粒沉降与去除。

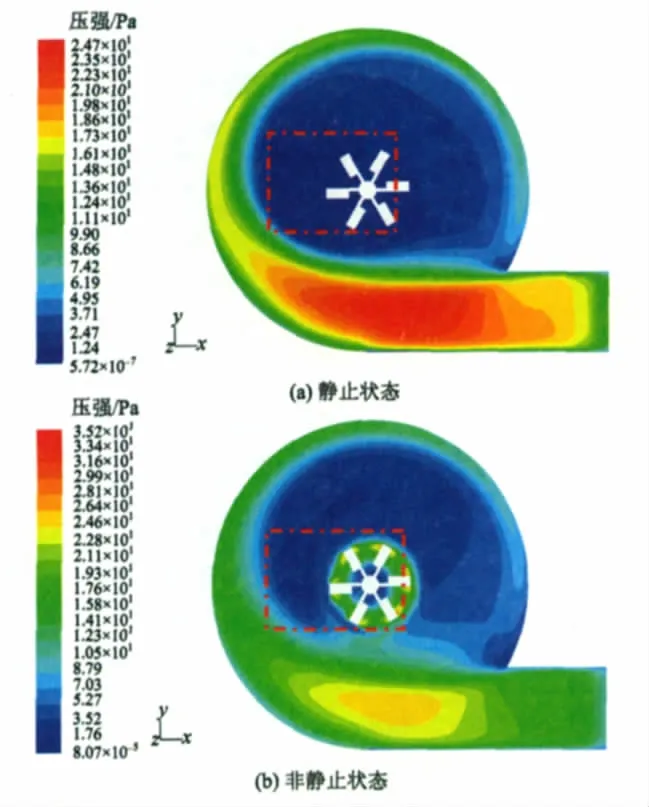
图7 搅拌桨静止和非静止时压强分布Fig.7 Pressure distribution in the stationary and non-geostationary mixing paddle

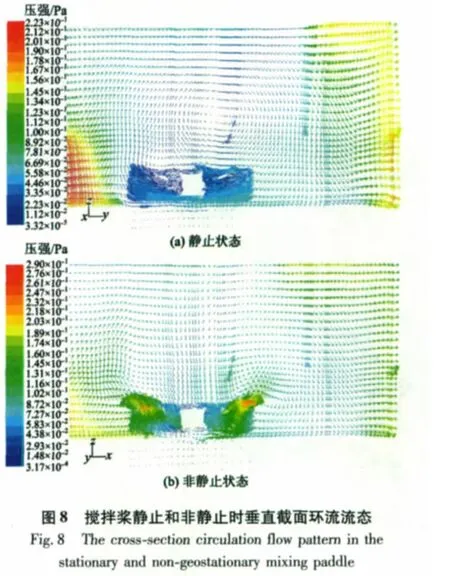
在搅拌桨静止时，一定的进水流速也会在池体内形成环流流态(主要取决进水渠结构及进出水的设计方式);搅拌桨在静止和非静止时垂直截面产生水平环流和轴向环流流态如图8所示。

3.3 搅拌桨旋转方向的变化对砂粒运动的影响

3.3.1 逆时针

搅拌桨逆时针旋转的垂直截面速度矢量与砂粒运行轨迹如图9所示。由图9(a)可知，当搅拌桨逆时针运动时，轴向环流呈逆时针流态，这将不利于砂粒的沉降与去除:一方面池壁附近的砂粒在沉降过程中将受到一定的阻碍作用;另一方面搅拌桨附近的流场不利于砂粒向池心移动。因此，在搅拌桨逆时针旋转时，大多数砂粒可能始终悬浮于池体内，而最终会随水流带走。

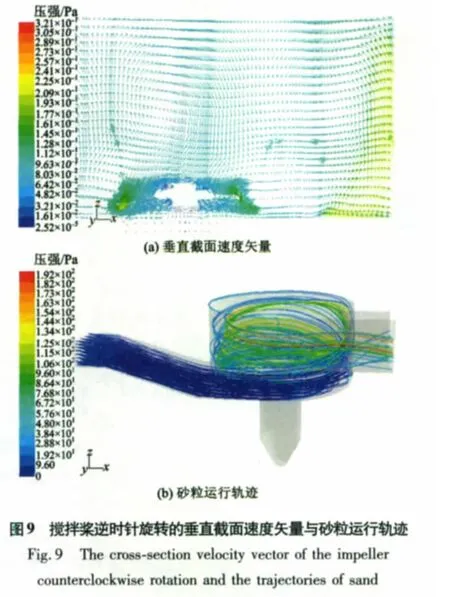
通过向模型中注入砂粒，基于液相流场的数值模拟结果，采用离散相模型对砂粒的运动进行计算，结果显示〔图9(b)〕，在沉砂池砂斗中砂粒量很少，反而在池体内及出口处存在较多的砂粒，其与垂直截面速度矢量图的分析相符，说明当搅拌桨逆时针旋转时，沉砂池内的流场不利于砂粒的沉降与去除;同时也说明搅拌桨转速对沉砂池中砂粒的去除有着一定的作用。

3.3.2 顺时针

搅拌桨顺时针旋转的垂直截面速度矢量与砂粒运行轨迹如图10所示。

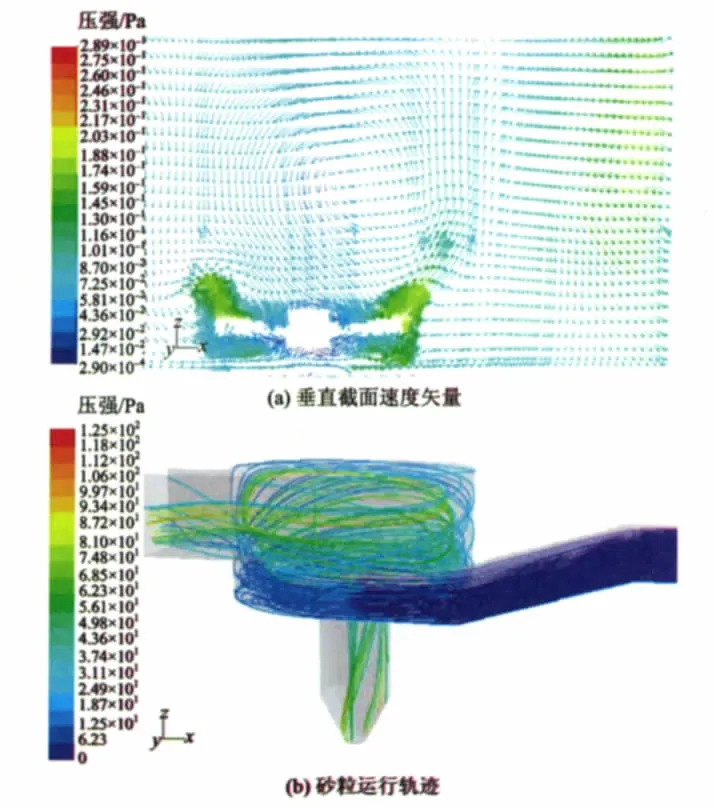
图10 搅拌桨顺时针旋转的垂直截面速度矢量与砂粒运行轨迹Fig.10 The cross-section velocity vector of the impeller clockwise rotation and the trajectories of sand

当搅拌桨顺时针旋转时，由图10(b)可知，水流夹带着砂粒沿着沉砂池底部周边进入池体内，在强制涡旋的作用下，一部分砂粒在水平环流与轴向环流的作用下，在砂斗中被捕集;而部分尺寸较小的砂粒则重新返回到水流中，在池体内经过若干个螺旋循环运动后，随水流由出口带走;结合图10(a)可知，与搅拌桨逆时针运动所产生的结果相比，顺时针旋转形成的轴向环流是顺时针流态，因此，当搅拌桨顺时针旋转时，池体内所形成的环流流态有助于砂粒的沉降与去除，且符合旋流沉砂池的运行特性。

4 结果与分析

4.1 搅拌桨运动与进水流速的关系

4.1.1 搅拌桨静止时进水流速变化对砂粒去除效果的影响

当搅拌桨静止时，进水流速(0.09，0.12，0.18和0.36 m/s)对砂粒去除的影响如图11所示。

图11 搅拌桨静止时进水流速对砂粒去除的影响Fig.11 Different water flow rate on the impact of sand removal efficiency for the stationary mixing paddle

由图11可知，在不同进水流速下，池体含砂率均较高，砂粒的去除率均较低，主要是由于进水水流所产生的轴向环流虽然可以使大多数砂粒沉降于池底，但进水流速所产生的轴向环流强度及影响范围有限，因此，砂粒的运动将受到限制，也进一步说明了搅拌桨转速对砂粒运动的重要性。

另外，由图11还可以看出，在进水流速较小时，池体含砂率较高，逃逸率较低;而在进水流速逐渐增大时，池体含砂率逐渐减少，逃逸率相应地增加。这是由于水流夹带着砂粒在沉砂池内以螺旋状前进，当进水流速增大时，水流进入到池体的射流强度将增大，所形成的涡旋强度也将随之增强，加之砂粒的运行路径也会明显缩短，使得部分砂粒来不及沉降而随水流由出口带走;当进水流速较小时，大部分砂粒虽然存在于池体内，但由于进水水流强度较弱，所形成的轴向环流强度并不能使得多数砂粒向池心移动。因此，进水流速过大或过小都不利于砂粒的沉降。

4.1.2 进水流速一定的条件下，搅拌桨转速变化对砂粒去除效果的影响

在进水流速为0.18 m/s的情况下，不同搅拌桨转速(13，20，26，30，40 和60 r/min)对砂粒去除效果的影响如图12所示。

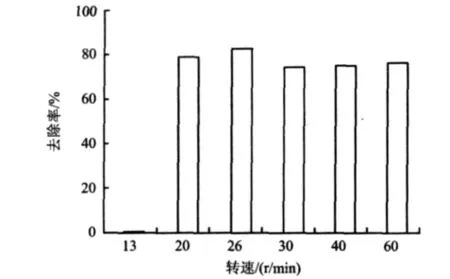
图12 进水流速一定时转速对砂粒去除率的影响Fig.12 Different influent velocity on the impact of sand removal efficiency for the constant flow rate

由图12可知，当进水流速为0.18 m/s时，砂粒去除率在搅拌桨转速为26 r/min达到最佳，而低于或高于该值砂粒去除率均降低。由离散相模型中砂粒的运动轨迹可知，在转速低于26 r/min时，砂粒的逃逸率与26 r/min时相近，但池体含砂率有着明显的差别，砂粒主要集中于池底位置(靠近搅拌桨附近)，这是因为砂粒向池心运动时，需要足够的力使砂粒移动，而仅依靠进水水流的作用，以及搅拌桨低转速的运动，不能达到有效去除砂粒，因为搅拌桨在低转速条件下，所产生的涡旋强度相对较小，使得搅拌桨附近大多数砂粒无法向池心移动;而当转速高于26 r/min时，砂粒的逃逸率降低，因为当转速增加时，搅拌桨周围也会形成逐渐增大的径向流［10］，其不利于池壁附近砂粒向池心的移动;同时池底内一部分砂粒在移向池心时，也会因较强的涡旋流，使部分砂粒重新回到水流中。

5 结论

(1)旋流沉砂池砂粒的去除，主要是基于强制涡旋流。在压力场方面，压强差将影响砂粒的运动;在速度场方面，池体内主要存在水平环流和轴向环流两种流态。

(2)当搅拌桨旋转运动方向不同时，沉砂池内所形成的轴向环流流场存在较大差异。当搅拌桨顺时针旋转时，产生的轴向环流流场符合沉砂池的运行特性，轴向流速有利于砂粒的沉降和池底附着砂粒向池心的移动;而当搅拌桨逆时针旋转时，产生的流场不利于砂粒沉降与去除。

(3)当搅拌桨静止时，进水流速过大或过小都不利于砂粒的沉降。进水流速过小，池体内会累积较多的砂粒;而进水流速过大，砂粒的逃逸率也随之增大。

(4)在进水流速一定时，搅拌桨转速的变化对砂粒的去除也有一定的影响。当转速较小时，产生的涡旋强度不足以将砂粒移向池心，因此砂粒去除率较小;而当转速逐渐增大时，形成的径向流和较强的轴向流不利于砂粒的沉降与去除。

［1］邹启贤，张金松，曲志军.沉砂池类型及其应用［J］.西南给排水，2005，27(4):8-11.

［2］李涛.沉砂池的设计及不同池型的选择［J］.中国给水排水，2001，17(9):37-42.

［3］高廷耀，顾国维，周琪.水污染控制工程［M］.3版.北京:高等教育出版社，2006.

［4］邵林广.圆形涡流式沉砂池除砂效率的探讨［J］.给水排水，1998，24(12):38-40.

［5］谭小铤.国外两种圆形沉砂池的讨论［J］.给水排水，1998，23(9):23-26.

［6］王雪原.Pista360°涡流沉砂池的特色与设计要点［J］.中国给水排水，2001，17(8):36-38.

［7］WANG X L，ZHOU S S.The numerical computation of grit chamber with rotational flow［C］//Bioinformatics and Biomedical Engneering(iCBBE)，2010 4th International Coference.Pascataway:IEEE Press，2010.

［8］栾闯.基于CFD的水电工程砂石废水旋流沉沙池的优化设计［D］.天津:天津大学，2009.

［9］李涛.处理砂石废水的旋流沉砂池内高浓度固液两相流数值模拟［D］.天津:天津大学，2010.

［10］陈乙崇.搅拌设备设计［M］.上海:上海科学技术出版社，1990.

［11］端木强.容器设计中搅拌装置的轴向力分析［J］.天津化工，2003，17(1):50-52.

［12］周国忠，王英琛，施力田.搅拌槽内三维流动场的RNG k-ε数值模拟［J］.北京化工大学学报，2002，29(2):15-19.

［13］王福军.计算流体动力学分析:CFD软件原理与分析［M］.北京:清华大学出版社，2007.

［14］ANIL W D.Introduction to computational fluid dynamics［M］.New York:Cambridge University Press，2005.

［15］VERSTEEG H K，MALALASEKERA W.An introduction to computational fluid dynamics:the finite volume method［M］.New York:John Wiley Sons Inc，1995.

［16］ANDERSON J D.Computational fluid dynamics:the basics with applications［M］.New York:McGraw Hill，1995.

［17］Fluent Inc.Fluent 6.3 user’s guide［M］.Harrisonburg:Fluent Inc，2006.

［18］于勇.Fluent入门与进阶教程［M］.北京:北京理工大学出版社，2008.

［19］叶瑞.新型旋流沉砂池砂粒去除效果的数值模拟［D］.合肥:合肥工业大学，2009.○