试论数学的文化奇观——兼谈文化和科学文化

周守仁

（四川省社会科学院，四川成都 610041）

试论数学的文化奇观
——兼谈文化和科学文化

周守仁

（四川省社会科学院，四川成都 610041）

广义的文化定义主要有“总和说”与“模糊说”两类。把“总和说”进一步扩展为“超广义说”，把“模糊说”修改为“自创生说”，将两者结合起来称做“超广义自创生文化说”。科学文化指科学本身以及科学与社会其他文化相互交融所形成的文化群类。数学文化指把自然、社会、思维等各个领域中的数量关系、空间形式、信息符号、能量运转、物质结构的哲理精蕴、艺术神采以其微妙深奥的规律化方式智慧地展现出来。数学的文化奇观的表现形式为深蕴的统一性、内增的复杂性、天成的艺术性和奇难的悬疑性等四个方面。

数学的文化奇观；统一性；复杂性；艺术性；悬疑性

一、文化、科学文化和数学文化的现代新释

当人们有幸迈入数学文化的殿堂，那琳琅满目、俯拾即是的数学珍宝，将以其无比的奇姿美态夺人心魄。如果能有幸获得些许珍宝在手，无疑会一生一世享用不尽。可究竟什么是数学文化呢？笔者才疏学浅，不敢妄加界定。但探索数学文化为本人的一大快事，也只好不顾被人指点之虞写出此文。

笔者自忖，若能首先使文化、科学文化、数学文化在概念解释方面逻辑一致，则不管对数学文化理念阐述如何，总可以有一个稳当的起步。文化这个概念是多义的，且很难定义。据统计，现有关于“文化”定义的表达已超过160多种，笔者不揣冒昧提出“超广义自创生”文化概念。

这里，直接从人们对文化的广义定义开始探讨。对文化的广义定义主要有“总和说”与“模糊说”两类。

例如，有人把文化当作物质财富与精神财富的总和，认为文化是人与自然、人与世界全部复杂关系种种表现形式的总和。还有人把文化看成是人类实践能力方式及成果之总称，等等。这些都是关于文化含义的“总和说”。另一些研究人员认为，“文化”是一个比较模糊的概念，它犹如许多细胞构成的一个整体，边缘不齐整，内涵不确定，外延也不确定，因此只能暂时给出一个模糊的、不完全确定的定义。这就是关于文化定义的“模糊说”。

笔者的看法是，把“总和说”进一步扩展为“超广义说”，把“模糊说”修改为“自创生说”，把这两者结合起来，称作“超广义自创生文化说”。笔者的这一看法直接表明文化具有无所不包的性质和自我生发的性质。这一看法可表述为：“超广义自创生”文化是指人类个体或群体的一切思想和行为及其一切自我生发的过程和结果。稍加展开地说，“超广义自创生”文化是与人及其发展同在的不断演化的复杂多样的意识理念及其体系、行为活动及其范式、物化实体及其场景。从一定角度来审视，上面表述了两项研析工作，前者是关于文化概念的逻辑操作，后者则是开掘文化理念的智能禀赋。与上述观点相对应，超广义自创生文化说有如下两个特征：

（一）超广义是最大可能的全面性，尽可能无筛漏。文化的定义不能是个有孔的筛子，否则就把本应是文化的要素或现象从筛孔漏出去。因此，对所有文化现象，应该无孔覆盖。如中央电视台举办的青歌赛曾把原生态唱法的代表者之一阿宝给忽略了，给漏掉了。“与人同在”这一表述是具有最大可能的全面性。例如，人一旦在母体中生成，就具有并表现出文化，如胎教文化。又如，野蛮与文明对立，但野蛮人也有自己的文化。再如，平常我们说文化分为先进文化、落后文化、腐朽文化（我在此加上一个平庸文化）。这就是说，腐朽文化也是一种文化，如同坏人也是人一样，不能把腐朽文化从文化范畴中排除出去。一个现象或事物是否是文化的，也不能只从是否有意义，有价值来划界。大家风范，不容置疑是一种个性的同时又有普遍意义的文化现象；但小人物的个人琐事，虽然平凡无味，但也是一种个性文化，只不过把它叫做平庸文化而已。总之，我们从“与人同在”的各种事物、现象中很难找出不是文化的东西。

（二）自创生表示文化是动态的，是有生命性的，是有根源、脉络和演化的。我们不能给文化以永远不变的具体特性。譬如，我们可以把腐朽文化“化腐朽为新奇”。对原来没有认知现在才发现的自然事物，赋予其一定创新文化的意义，等等。

此外，上面提到的关于文化定义的“模糊说”，它注意到文化范畴的不确定性。这种不确定性是文化本身内在的自我生成的不确定性。特别是对个性文化而言，其自创生的不确定性特别复杂。我们知道，在审美领域有所谓“谈到趣味无争辩”，与其相类似，在文化观念上也有“谈到文化各自说”。

由上述可见，“超广义自创生”文化概念可体现出文化演化过程和结果的统一、历史和现实的统一、根源和发展的统一、要素和整体的统一。

接下去简扼地说一下现代科学文化的实质内涵。科学本身即是一种文化，而科学文化则是指科学本身以及科学与社会其他文化相互交融所形成的文化群类。它是人类文化的重要组成部分。

按照方才关于文化的论述，对科学文化应作如下阐释：科学文化是人们在进行科学实践活动和其他社会实践活动中，由于探索未知、创新研究、发现真理、把握规律、生产知识等而形成的不断演进的包括科学本身在内的意识理念及其体系、行为活动及其范式、物化实体及其场景。现代科学文化的实质内涵，是由当代大科学决定的科学精神与人文精神、理性与非理性、求实与创新、真与善、美等辩证统一所形成的科学意识理念体系、科学行为活动范式和科学物化实体场景。

数学文化无疑是一种科学文化，它的文化特征充满了令人惊奇、赞叹和向往的魅力。笔者试把数学文化的意义和基本特点做出如下的表述。

数学文化把自然、社会、思维等各个领域中的数量关系、空间形式、信息符号、能量运转、物质结构等的哲理精蕴、艺术神采以其微妙深奥的规律化方式智慧地展现出来。它是具有无限生命力的自创生、自创新的文化，并始终与人同在。

数学文化的基本特征在它独具的复杂多样的数学意识理念及其体系、数学行为活动及其范式、数学物化实体及其场景中充满奇观的不断表达。

数学文化的意识理念体系包括数学史上丰富的数学哲理、数学思想和数学方法。在这里只举一些例子供人们思考。

在数学文化思想史上，以罗素（B.Russell 1872～1970年）、弗雷格（G.Freg 1848～1926年）等人为代表的逻辑主义学派（Logistic school），以克罗内克（L.Kroneker 1823～1891年）、布劳威尔（L.E.J.Brouwer 1881～1967年）等人为代表的直觉主义学派（Intuitionist School），以希尔伯特（D.Hilbert 1862～1943年）为代表的形式主义学派（Formalist School），以魏依（A.Weil 1906～？年）、歇瓦莱（C.Chevalley 1900～1984年）等人为主的布尔巴基学派（Bourbaki School），以我国学者郑毓信（1944～）提出的数学真理的层次结构（逻辑合理性、模式真理、现实真理）［1］等数学文化意识理念，对数学学科、数学文化的发展都在不同程度上起了积极的推动作用。

数学文化的行为活动范式主要是指数学爱好者、数学工作者及数学家们在对数学的欣赏、学习和研究中所表现的习惯、举止、情趣、风貌等方面的共性特征。例如，严谨的求证学风、顽强的解难毅力、激发的逻辑乐趣、痴迷的探秘追求以及忘我的理性思考等。他们这种看起来似乎是着魔的神态，却具有那些停居于数学世界以外的人们所难以理解的、难以想像的情智魅力。至于数学文化的物化实体，至少集中在两个方面：一是作为数学计算工具和载体的计算机；一是作为数学应用领域的大科学技术世界，它包括自然科学、社会科学、人文科学、思维科学、工程技术和教育、医卫、政治、经济、法律、日常生活等的数学意义与价值的物化性和精神物化性的具体体现。例如，从第一方面来看，当今世界都在争相研制极高性能的超级计算机，这实质上就是在大力建设数学文化的物化实体场景。超级计算机是由上百上千的处理器组成。从文化角度来说，它是现代数学文化奇观的一种物化实体。在去年，即2011年，日本研制的K Compute以每秒运算峰值可达1.05亿亿次而成为全球最快速的超级计算机，它也是迄今为止人类首次超越1亿亿次计算的超级计算机。中国研制成功的“天河一号”超级计算机运行速度也已达到每秒2 573万亿次。这些超级计算机的研发不仅显示了计算机科学技术的惊人发展，同时也表明了数学文化的长足进步。

二、数学文化奇观的探幽阐微

数学的文化奇观根源于数学文化的自创生、自出新这一根本性质。依照数学文化奇观的表现形式，可把它们归纳为以下几点：

（一）深蕴的统一性

众所周知，数学是有机的统一整体。但数学的统一性并非是终极的静态目标，它是一种具有生命的可生发的统一性。例如，费马（P.de Fermat 1601～1665年）和笛卡尔（R.Descartes 1596～1650年）把代数与几何统一起来，即把代数方程和几何图形联系起来，从而创立了坐标几何（解析几何）。当代数与几何各自无关发展时，既缓慢又无生气。但当二者统一起来时，也就是一方面用代数语言表示几何概念，另一方面又用几何来诠释代数语言，这样就形成了具有鲜活生命的统一性的坐标几何，从而推动了17世纪数学的巨大发展。到了20世纪，现代抽象代数兴起，它包括抽象群、环、域等概念。以抽象代数为基础的代数几何更有广阔的发展前景。具体的事物无疑具有生动性，但抽象的数学事物同样具有，甚至具有无比的生动性。笔者认为，抽象的统一性概括了多样性和众多特殊性，这统一性一旦远离它生成的基础——多样性和特殊性，那就可能走向没有生命力的歧途。因此，数学的自创生、自出新的抽象统一性必须植根于它的非抽象的能给予其取之不竭生命活力的生成源泉。克莱因（M.Kline）曾告诫说，“抽象代数已经毁坏了它自己在数学中所起的作用”［2］。当然，这并非对抽象代数的否定，而是提醒在抽象代数领域里的数学工作者应熟悉抽象结构的来源，要关心其结果对具体领域的应用［2］。

又如，在第21届国际数学家大会上，颁布的四项菲尔兹（Fields）奖分别授予美国的E.Witten、新西兰的V.F.R.Jones、苏联的B.Γpинфeлъд和日本的森重文。这次颁奖表明了各数学分支的相互关系，蕴含着数学内在的统一性，并证实了数学统一性所彰显的生动性和鲜活性。E.Witten在其研究成果中重新发现了Jones多项式；编辫群出现在B.Γpинфeлъд、V.F.R.Jones和E.Witten的著作里；森重文的三维代数簇研究，涉及到物理超弦问题与曲线簇上代数几何问题的转译对应性［3］。

再如，20世纪著名数学家迈克尔·弗兰西斯·阿提雅（M.F.Atiyah）曾于1966年莫斯科国际数学家大会上获菲尔兹奖，后来担任过英国皇家学会副主席、主席。他与另一位数学家辛格（I.M.Singer）合作，证明了“阿提雅—辛格指数定理”（Atiyah－Singer Index Theorem）。这一定理表明，“椭圆算符的解析指数等于拓朴指数”。他们在证明这个定理的过程中用到了很多重要的数学工具，如K理论，即线性代数的代数拓朴，并把握住具有一般意义的狄拉克算符等等。阿提雅—辛格指数定理是一个普适性程度很高的基本定理，它把分析与拓朴在深层次上统一起来，它在偏微分方程、随机过程、黎曼几何、代数几何、代数拓朴以及数学、物理等领域都获得广泛的应用。有人赞誉阿提雅是站在顶峰的拓朴学家，也有人认为，阿提雅—辛格指数定理就如同英国索尔兹伯里平原上的巨石群一样将永远让历代人们络绎不绝地前来瞻仰。阿提雅—辛格指数定理对数学统一性的贡献是难以估量的。许多数学家都在忙于计算指数，不容置疑，这是完全应该做的。但如何去探掘深蕴在这个指数定理之中的数学统一性，将更是有价值、有意义的科研课题。

最后提一下，模（Module）概念是对数学统一性非常有用的概念。模是具有算子环的Abel群，是域K上的线性向量空间，是用环代替K时的推广。它生发繁衍出诸如代数曲线上的模、曲线族的模、系数模、复数的模、实数的模、有表示的模、带算子区的模、不带算子区的模等等。前些年日本的数学家研究并发展了D—模，这是可用具有解析系数的偏微分算子作乘积的模。D—模为分析、代数、几何（或拓朴）三个核心数学领域架起了桥梁，使数学家们逐渐清晰地看出深蕴于数学本质内的统一性。

（二）内增的复杂性

数学在其自身的极为深广的量的关系领域内，又有着更深层次的质与量的相互联系。人们在数学研究过程中，发现了由某些自变量的变化引起数学复杂性的变化。这种复杂性一方面是客观的、数学内在的复杂性，另一方面也是人们意识理念对数学世界积极反映的结果。下面通过一些例子来说明作为数学文化奇观的内增复杂性。

第一个例子是从较小的自然数到很大的自然数再到无穷大。

设一个几何级数为1＋2＋22＋23＋24＋25＋26求其和为27－1＝127。这里2的指数n最大为6，如果这个几何级数2的指数n最大为63，则1＋2＋22＋23＋24＋……＋263＝264－1＝18 446 744 073 709 511 615，相比之下，后者比前者要大到天文数字。

若进一步，n趋近于无穷大，即n→∞，则此级数和更是无穷大。

这里的自变量是自然数n，随着n的增大，使得这一几何级数的复杂性（级数和的数目）不断骤增。

此外，这个简单的例子还说明，有限和无限的复杂性是截然不同的，很多迷人的数学文化奇观大都和无限大（或无限小、无限多）有关。

第二个例子是涉及无穷范畴的一些数学理念。当考察无穷级数时，数学家们探讨了无穷级数的收敛和发散，以及判别收敛的充分必要条件。在研究无穷级数的过程中，曾出现过很有生命力的预见性思想，那就是发散级数可以用来对函数进行数值逼近，级数可以在解析运算中代表函数，甚至发散级数也可能有这样的用处［2］。

当踏入数论领域，我们至少会看到无穷概念施展的新奇的复杂性。在初等数论中，人们很容易接触到“素数的个数是无限的”这一定理。该定理的证明比较简单。但进一步把无穷概念放在某些猜想之中时，看似简明的论断却难以证明，甚至至今也没有找到答案。例如，常被人们提及的哥德巴赫猜想，它是这样一个猜想：“大偶数可表为两个素数之和。”如果仅仅是对某个或某些指定的偶数而言，不论它们有多大，总可以用超级计算机来确证这个猜想。但是若对无穷个偶数而言，即使当今最快速的超级计算机对此也无能为力。因为没完没了地让计算机运转下去，最终答案也不会出现。所以，从无穷概念的魔力作用来看，哥德巴赫猜想是向人类高超情智挑战的数学内增复杂性的一大难题。也许，在代数数论、解析数论之外，可能会以突现出新的数论奇观的理论和方法拿下这颗数学神坛上的明珠。

再举两个能说明数学内增复杂性的几何学方面的例子。

首先是一个简单的例子，在一个直线上的原点只有两个方向，而在一个平面上的原点却有无穷多个方向。它表明，以维数作为自变量，当它仅仅从一维转到二维时，就出现由有限变为无限的陡增的复杂性质变。这个一目了然的简单例子，会促使人们对高维几何学的遐想和猜测。因此，这个例子是平凡的也是非凡的。第二个例子要更为复杂些。一个直线可按仅有的一种方法闭合（成为一个圆），但一个平面却能闭合成许多不同类型的曲面。譬如，通过球极平面射影闭合为一个球面，通过使一个正方形各对边的粘合闭合成一个环面等。当从二维转到三维时，将出现某些新现象，此时，一般说来各种有意义的问题变得更困难了。如在二维的情况下，可描述所有可能使平面闭合的方法，但在三维的情况下，这个问题还未被解决［4］。

（三）天成的艺术性

有人说，数学是心灵的自然科学。但笔者认为，数学似应该叫做大科学（包括自然科学、社会科学、人文科学、思维科学等）的量域艺术。人们运用在社会生产、生活以及大科学等实践中不断发达的情智和逻辑演算能力去反映、研究和把握客观世界的数学真理。数学真理不是为表现人们心灵的智慧而存在，它激发心灵智慧，并让心灵智慧和客观的数学真理渐近一致。我们为数学家在数学领域惊人的创造性发现而欢欣若狂，这只能证明人的心灵智慧具有认识包括数学真理在内的客观规律的能动性、创造性和获真性。当然，人们反映客观事物及其规律性的过程和形式是多种多样的，主观与客观之间并非只有直接对应的单一形式，譬如说，虚数单位，在它被人们发现之初（即当考察方程x2＋1＝0时，由于没有实数能满足这个方程而导入它），其实在性与实用性大受怀疑。后来，人们把能够按一定规则进行加减乘除、乘幂与开方运算的平面自由向量系理解为复数集合，从而建立了复数与平面上点之间的完全对应关系。到此时，通过复数的应用，人们已看到了虚数的价值。要想较为全面的分析虚数的价值，大致应从三个方面来考察。首先是虚数的哲学价值，它表示了数学概念与客观实在的多样对应关系；其次是虚数的科学价值，它通过复数而获得广泛的重要的应用；再次是虚数的艺术价值。虚数还有艺术价值吗？人们会用诧异的眼神向这一提法发问。笔者试用一个例子，把虚数魔术般的作用，即它带有魔术意味的艺术价值展现出来。

图1 巧妙的虚数例证

虚数的艺术价值由天成的艺术性与人为的艺术性两部分组合。譬如说，人们发现了金矿，不能说金矿是人为制造的。但工匠制作精美的金饰品（金手镯、金戒指等）则既包含金的天然价值，也包含金饰品的人工价值。虚数的天成艺术是由本身固有的奇异性和它与实数的关联所决定。在复数计算时，其实数部和虚数部是分别计算的。但i2＝－1，却把实数与虚数联系起来。上述图1表示的例子，将虚数有别于实数的奇异性及它与实数的关联性，都在运算中显示出来。负数不能作为任何实数的平方数，这本来就限制了开平方的运算，但这虚数的出现却偏要使负数成为它的平方数，从而冲破了开平方的运算限止，让人们大吃一惊。于是这就成为虚数的奇异性。但同时它又包含了虚数与实数的关联即i2＝－1。我感兴趣的是虚数固有的由它的奇异性和它与实数的关联所共同产生的天成的魔术般的艺术性。图1作为人为设定的例子，其所说明的M点坐标为虚单位i且与a、b无关的巧妙性质，显然包含关于虚数的人为艺术性。笔者认为，对此应给予更深入的研究，此处无非是抛砖引玉而已。

图2 非刚体变换的八面体群对称性的“多面体嵌入”

数学中的对称也有天成的艺术性与人为的艺术性之分。对于人类来说，千姿万态的雪花可能是最直接感知的具有素洁和对称性美的天成艺术品。其正六角形结构形式，让人们世世代代赏心悦目。当把积雪堆制成雪艺术品时，其随人所欲的对称性将是一种人为对称性艺术美。然而，这里的人为对称艺术性，就其结构原型来看，仍然属于数学中天成的对称艺术性。下面举一个较为复杂的对称性例子。笔者将它视做数学中具有人为艺术性的结构。如图2所示，是一个具有非刚体变换的八面体群对称性的“多面体嵌入”。

它被用作笔者所著《“对称—整合”思维模式》一书的封面图案，它是一种隐对称性。它由288个四边形、144个顶点组成，在每个项点有8个四边形相连。它既具有精巧的较为复杂的对称性，又具有包络的“嵌入整合”的性质，概括形象地表达了该书的主题——“对称—整合”的含义［5］1。笔者之所以把图2所表达的对称性视作人为的对称艺术性，是因为它在现实中没有对应物。该对称性不像雪花的正六角形对称结构那样具有自然物本身天成的对称艺术性。

从事群论（直观地表达对称性的数学工具）研究的数学家们曾完成有限单群分类及其证明的工作。据资料记载，从20世纪40年代末到80年代初，有100多位数学家花费了30多年的时间，写出数学史上罕见的长达15 000多页的浩繁篇幅，才完成此项研究工作［5］136。在有限单群分类中有26个不规则的散在群，其中Fischer-Griess大魔群（约有8.08×1053个群元素，是最大的散在群）是人们已知的世界上最优美、最丰富的对称性。但是，它怎样以其尚且未知的奇异方式筑入到宇宙的真实结构中［5］4，那似乎还是遥不可及的事情，所有对群论及其应用感兴趣的人们将对此翘首以盼。笔者认为，大魔群是群论研究的一个产物，与图2中的对称性只是人为构造的不一样，不过，它是否有客观对应物尚不得而知。所以，大魔群究竟是具有天成对称艺术性还是具有人为对称艺术性，应该是一个有待今后群论研究结果来确证的未知问题。

数学家及数学爱好者都喜欢数学公式的简洁性。简洁性是科学美的一个重要表现形式。《The mathematical intelligencer》杂志在1988年第3期上发表了一组24个数学公式和定理，请读者给这些公式或定理从0到10打分，对它们的数学美进行比较［6］，参加讨论的人对所列24个公式和定理是否是美的、数学美的标准及他们的审美观等都不同。笔者认为，对科学数学美的审视标准至少应有以下几点：理论价值和意义，应用贡献的广度和深度，创新性和简洁性。后来，在该杂志1990年第3期上公布了68个评分者的平均值，并以多少排了序［7］。因篇幅所限，这里只列出前三名（第二、三名各有两个并列）：

（欧拉公式：eiφ＝cosφ＋i sinφ，当φ＝π时，有eiπ＝－1）

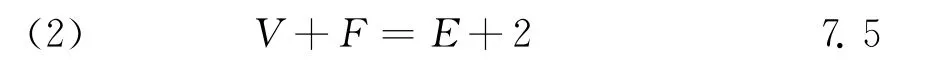
［多面体的欧拉公式，对于任意多面体（即各面都是平面多边形，并且没有洞的立体），假设F、E和V分别表示面、棱（或边）、角（或顶）的个数，则有V＋F＝E＋2］

（四）奇难的悬疑性

纵观数学发展的历史，曾出现过许多奇难的悬疑问题。最早有所谓初等几何作图不能的三大问题，即立方倍积、三等分任何一角及改圆为方。直到距第一次提出这三个问题2 000多年后的19世纪才证明，用无度尺和圆规做工具是不可能解这三个问题的。这个结论有赖于伽罗华群代数方程求解的准则及π是超越数的证明等数学研究成果。

20世纪伊始，希尔伯特（D.Hilbert 1862～1943年）提出曾引起众多数学家为之奋力求解的23个数学问题一览表（即1900年的希尔伯特一览表〈Hilberts list of 1900〉）。后来，其中有几个问题已获解决或部分解决。如连续统假设、两点间以直线为距离最短线问题、拓朴学成为李群的条件（拓朴群）等问题［8］。

在20世纪末，菲尔兹奖获得者Steve Smale发表了包括18个数学问题的《下一世纪的数学问题》一文。在这18个问题中，有黎曼假设、庞加莱猜想、P＝NP？二维球上点的分布等数学问题［9］。

我们知道，提出已逾百年的拓朴学上最重要问题之一的庞加莱猜想已被攻克。在众多数学家对这一问题研究成果积累的基础上，中山大学的我国数学家朱熹平和美国里海大学的曹怀东于2006年6月在《亚洲数学期刊》发表了他们的完整证明。

在这里，笔者只想对另一个研究历史长达350年左右的费尔马大定理（Fermat′s Last Theorem亦译为“费尔马最后定理”）问题的解决谈一点粗浅的感受。费尔马大定理可表为：不存在整数x、y、z和n，其中n＞2，xyz≠0，使得xn＋yn＝zn。

英国数学家维尔斯（A.Wiles）在经历了对费尔马大定理有所错误的研究之后，终于在1994年10月以无可否认的新的证明解决了费尔马大定理这一奇难的悬疑问题。他以《模椭圆曲线与费尔马最后定理》（Modular elliptic and Fermat’s Last Theorem）为题，与同一位学生合写的题为《某些赫克代数的环理论性质》（Ring-theoretic properties of certain Hecke algebras）两篇文章同时发表在美国《数学年刊》1995年第3期上。该期只发表了这两篇文章，共127页（第一篇108页，第二篇19页）。第二篇文章旨在提供由考虑存在完全交叉的某些最小赫克代数所确证的，维尔斯曾用到的一个假设的关键部分［10］。维尔斯此次在《数学年刊》上发表的文章，毫无疑问将载入数学发展史册。维尔斯开始曾试图利用谷山—志村（Taniyama-Shimura）猜想（这一猜想说的是：所有椭圆曲线均是模曲线）来证明费尔马大定理。但这一尝试在接近结束之时遭到挫折。为了完成证明，维尔斯又试图构造一个欧拉系统，但是这看起来最合乎逻辑的处理方法，用它来解决问题却是非常困难。后来他绕过欧拉系统及构造所用的棘手方法，而在新的结尾采用了从前他曾放弃过的赫克代数方法。这是一个精巧而漂亮的方法［11］。

有人把费尔马大定理比喻为一个长长的艰险的洞穴通道，它终止于无法看见的死巷。探讨它的证明，就如同在这个洞穴内的攀行运动。但维尔斯对费尔马大定理的证明，却像打开了一个全新的拜占廷式的卧室、回廊和迷宫似的通道，经过其中一个细细的缝隙返回到原先死巷的入口［12］。笔者觉得，这是一个令人玩味无穷的比喻。它大致描绘了维尔斯在证明费尔马大定理过程中的创造性思考。笔者认为它给人们以一种新的方法论。笔者称其为是绕行寻路方法、暂离逻辑方法和累积聚成方法的有机结合。绕行寻路的方法是指绕过不能直接克服的困难而继续前行寻路的方法；暂离逻辑的方法是指维尔斯没有僵硬的迷恋合逻辑性；累积聚成的方法则是指维尔斯不是完全独出心裁，他是在前人研究费尔马大定理所获成果基础上独辟蹊径。

除了庞加莱猜想、哥德巴赫猜想、费尔马大定理这类数学史上著名的奇难的悬疑问题，还有一些始终使数学家们为之倾倒的既熟悉又奇特的问题，如数学分析中的无穷小概念。我们知道，通常的经典数学分析叫做标准分析。上世纪60年代美国数理逻辑学家罗宾逊（A.Robinson，1918～1974年）提出并建立了非标准分析的数学理论。他认为，无穷小既然不是一个数，那么可否把实数系R扩大成新的数系R＊，即扩大到非标准域（超实数集合）。在非标准分析中，变量不仅可取R中的数，而且还可推广到无穷小量和无穷大量。根据非标准分析理论，实数轴上的点是内部有结构的点。非标准分析可将一些定理的证明简化。但是要想真正把非标准分析理解透，也并非易事。同时，由于非标准分析的数理逻辑方法很繁琐，且与标准分析等价，因此人们对它也多有微词。

在20世纪末，一位叫做J.M.Henle的数学家在《The Mathematical Intelligencer》上发表了一篇题为《非—非标准分析：实无穷小》一文。文中Henle的观点是这样的：设a为一序列，如果对于所有正实数d，｜a｜＜d，则序列a就是无穷小的。对于无穷小的a，我们写成a≈0。如果对于某些实数r，｜a｜＜r，我们则说a是有限的或有界的。如果a≠0，且a≈0，则序列a是无穷小。这里，用a表示一个序列｛an｝，n∈N。

我们巧妙地处理实数序列，大多数情况下把它做为数来处理，可以使它们相加减，并把它们放在函数之中，但它们不是数［13］。

Henle的“非—非标准分析”的数学价值如何，应由数学家及广大数学工作者通过数学实践来查验。笔者只是从数学文化的角度，认为“非—非标准分析”的提出有助于加深对无穷小概念的进一步探讨，它至少丰富了人们关于“无穷小”思维的内涵。

在物理学中，有所谓“上帝不会掷骰子”、“上帝把骰子丢到人们看不到的地方”等说法。实际上，在数学中确实存在着内随机性。例如一个特殊的丢番图方程KX2＝2K2Y。当K＝1时，有X2＝2Y；K＝2时，有2X2＝8Y；K＝3，有3X2＝18Y；K＝4，有4X2＝32Y……丢番图方程KX2＝2K2Y有整数解（X≠Y）的K值的变化是不可预测的。这就是丢番图方程的内在随机性。

在计算机科学中，有一个不可判定的停机问题，即试图设计一台图灵机来判定一个图灵机对任意输入是否最终运行停止是不可能的。停机问题的不可判定性相当于停机概率在算法上是随机的结果。

哥德尔（Kurt Gödel）的第一、第二不完全性定理分别指出数学中内在的不完全性和不可证明性，笔者认为，内在随机性也可叫做既约不确定性，它是事物本身所固有的。例如，模糊数学中的类属关系的不确定性；混沌动力学中，迭代方程的迭代结果分布关系的不确定性；超越数π≈3.141 592 6……，其小数点后任意位置与它上面数字之间对应关系的不确定性；多向转化的临界区域、多边共存的结合部位、多层次交叉的缠绕范围、多尺度耦合的性态行为等所表明的动向关系的不确定性，都蕴含着深刻的数学的内在随机性。数学的内在随机性是数学的一大奇观，它令人要么忘而却步，或徘徊不决，要么穷追不放。这里面的奇难悬疑性，只有那些具有坚韧不拔的意志、非凡过人的情智并能锲而不舍实践的数学工作者及爱好者，才能探得一些真谛。

此外，笔者在《“对称—整合”思维模式》一书中，曾试图用对称破缺“三分态”对罗素悖论加以解释［6］189－192。笔者还想通过把抽象推论与具体实在相结合的方式去消除向选择公理挑战的“分球怪论”的赝悖论，即把关于无穷集的一个定理——一个集是无穷集的充要条件是它能和自己的某一个真子集对等——与两个实体之间的全同区别开来。因篇幅所限，这里不详述。

数学的文化奇观数不胜数，本文所列无非一孔之见，且笔者水平低下，阐解之中舛误难免，特恳请读者指错纠偏，不吝赐教。

［1］ 徐利治，郑毓信.略论数学真理及真理性程度——兼评怀特海的《数学与善》［M］//邓东皋，孙小礼，张祖贵.数学与文化.北京：北京大学出版社，1999：20- 22.

［2］ KLINE M.古今数学思想［M］.上海：上海科学技术出版社，1981（4）：257.

［3］ HINDRY M.1990年的Fields奖章——今年在京都颁布的四项Fields奖，显示了数学基础的统一和持久性［J］.数学译林，1991（3）：243-246.

［4］ ATIYAH M F.Tends in pure mathematics［M］//《Micheal atiyah collected works》Vol.1.265-266.

［5］ 周守仁.“对称—整合”思维模式［M］.成都：四川教育出版社，1993.

［6］ WELLS D.Beauty in mathematics［J］.The mathematical intelligencer，1988（4）：31.

［7］ WELLS D.Are these the most beautiful？［J］.The mathematical intelligencer，1990（3）：37.

［8］ 张光远.近现代数学发展概论［M］.重庆：重庆出版社，1991：92-96.

［9］ SMALE S.Mathematical problems for the next century［J］.The mathematical intelligencer，1998（2）：7-15.

［10］ TALOR R，WILES A.Ring-theoretic properties of certain hecke algebras［J］.Annals of mathematics，1995（3）：553.

［11］ LEUTWYLER K.再次巧胜费马［J］.Scientific american（中文版），1995（6）：71-72.

［12］ BROWN P G.No margin would contain it［J］.The sciences，1993（5）：7-9.

［13］ HENLE J M.Non-nonstandard analysis：real infinitesimals［J］.The mathematical intelligencer，1999（1）：67-73.

On Cultural Wonder of Mathematics——Discussing Culture and Scientific Culture

ZHOU Shouren

（Sichuan Academy of Social Science，Chengdu Sichuan 610041，China）

A broad definition of culture mainly includes the summation theory and the vagueness theory.The summation theory can be expanded into the super-generalization theory and the vagueness theory can be transformed into the autopoiesis theory.The two theories combined are called the cultural theory of super-generalization and autopoiesis.Scientific culture refers to science itself and the mixtures of science and other cultures.Mathematical culture shows the lawfulness of philosophy and artistry in quantitative relation，spatial form，information symbols，energy motion and physical structure of nature，human society and thought.Cultural wonder of mathematics is characterized by unity，complexity，artistry and suspense.

cultural wonder of mathematics；unity；complexity；artistry；suspense

B804

A

1673－0453（2012）01－0011－08

2011-10-10

周守仁（1934－），男，吉林长春人，四川省社会科学院研究员，中国自然辩证法研究会全国理事，四川省自然辩证法研究会副理事长，成都市自然辩证法研究会名誉理事长，主要从事自然辩证法研究。

吴 言）