锥形纳米金属线太赫兹波聚焦特性研究

梁华伟，阮双琛，张 敏，苏 红

深圳大学电子科学与技术学院深圳市激光工程重点实验室先进光学精密制造技术广东普通高校重点实验室，深圳518060

太赫兹波通常指频率在0.1 ～10.0 THz (1 THz=1012Hz)波段的电磁波，其电磁波谱位于微波与红外辐射之间，在生物医学、样品检测、无线通信等方面具有广阔应用前景［1-4］.

与光波相比，THz 波也有一定的局限性. THz波波长较长，由于衍射极限的制约，用其进行检测及成像时，分辨率较低，通常在毫米和亚毫米量级. 为提高分辨率，需对THz 波进行超聚焦，即将THz 波聚焦到远小于波长的程度［5］，为此，2006年，Maier 等［5］从理论上研究利用锥形周期性波状金属线实现THz 波微米量级超聚焦. 但由于该波状金属线在制作上困难，因此实验中难以实现. 2008年，本课题组提出利用光滑锥形金属线实现THz 波微米量级超聚焦的理论，并给出THz 表面等离子激元(surface plasmon polaritons，SPPs)在该金属线上传输的解析表达式［6］. 2009 年，Mittleman［7］和Awad［8］分别在实验上将THz 波聚焦到微米量级，实现THz 波超聚焦.

通过对锥形金属线上THz SPPs 传输特性的深入研究发现，利用锥形金属线不仅可以实现上述THz 波微米量级超聚焦，而且可以实现THz 波纳米聚焦［9］，即将THz 波的焦斑压缩到纳米尺度. 该研究成果一经发表就受到广泛关注［10-11］. 本研究详细探讨THz SPPs 在锥形纳米金属线上传输时的光场分布和强度变化特性，为实验中实现THz 波纳米聚焦提供理论依据.

1 基本理论

对于放置在空气中的一个柱形金属线，若仅考虑轴对称模式，则电磁场仅有3 个分量，即轴向电场Er、纵向电场Ez和切向磁场Hφ［12-13］. 场分量为

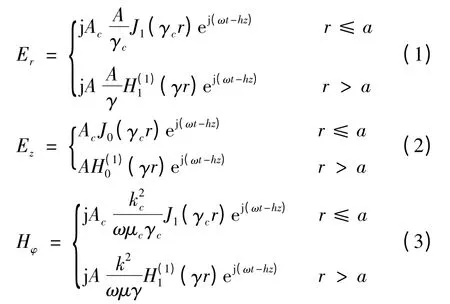
其中，h 是传播常数;a 是金属线半径;ω 是角频率;J0和J1分别是0 阶和1 阶贝塞尔函数;H(1)0和H(1)1是0 阶和1 阶第1 类汉克尔函数;A 和Ac为待定常数.

金属线内部和外部的波矢分别为 kc=(ωμcσc)1/2e-jπ/4和k = ω(εμ)1/2. 其中，ε 为介电常数;μ 为磁导率;σc为电导率. 参数γc和γ 分别为

由边界条件可知，Ez和Hφ在导体表面连续，因而可得如下特征方程

基于上述特征方程，可以求出传播常数，进而求出THz SPPs 在柱形金属线上的传输特性.

锥形金属线的外形和采用的坐标如图1. 对于锥形金属线，若其锥度较小，则可将其看做无数个柱形金属线的组合，因此它的传输特性可借助于柱形金属线的特征方程求解.

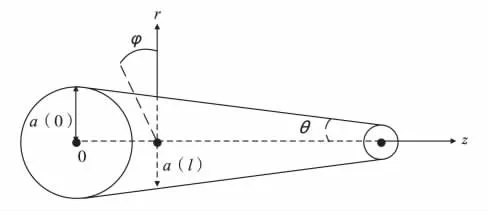
图1 锥形金属线波导Fig.1 The conical metal wire waveguide

对于锥形纳米金属线，若其半径小于金属趋肤深度［14］，则特征方程(6)可简化为

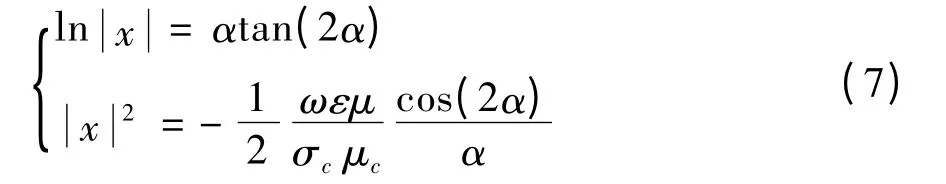
当THz SPPs 沿z 方向传播长度l 时，横截面上峰值电场的变化可由下列方程描述［9］

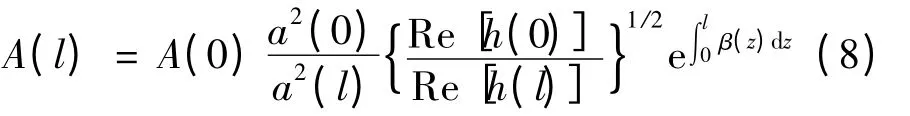
将式(8)称为锥形纳米金属线THz SPPs 表面场变化方程.

基于该方程可求出金属线表面任意位置的电场和磁场振幅，再利用式(1)～式(3)，可以求出金属线上任意横截面上的电场和磁场.

在传输过程中，THz 波强度的变化为

其中，β 为损耗系数;I0为金属线起始位置的THz SPPs 强度.

2 场分布

对于频率为0.1 THz 的电磁波，若其在不锈钢纳米线上传输，则根据方程(7)，可以求出γa =1.171 ×10-4ej0.8417，进而求得传播常数为

根据γa、h 及式(1)～式(3)，可以求出电场和磁场分量分布. 由于模场是轴对称的，所以只要知道一个方向上的分布，就可以知道整个横截面上的模场分布. 图2 给出当金属线半径为1、10 和100 nm时，横截面上任意径向的磁场分布.

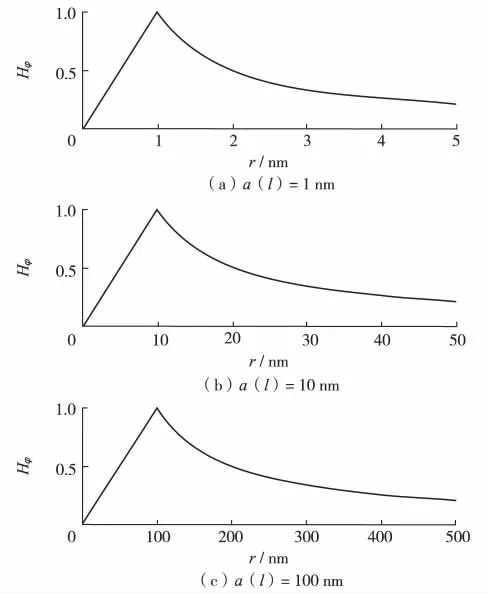
图2 金属线半径不同时，横截面径向上的磁场分布Fig.2 Different magnetic field distributions for metal wires with different radii

由图2 可知，当金属线半径不同时，横截面上的磁场分布规律一致，都是中心为0，然后向四周增强，在金属线表面强度最强，然后再减弱的环形焦斑. 但是，金属线半径不同时，相应的环形焦斑大小不同. 如果定义模场振幅降为峰值的1/e 之间的宽度为环形焦斑的宽度，则对于半径为纳米量级的金属线，焦斑宽度约为半径的2.4 倍. 这是因为，由式(1)～式(3)可知，当金属线半径为纳米量级时，金属材料、THz 波频率等参数对焦斑大小的影响可以忽略. 因此，为进一步压缩太赫兹波纳米焦斑，应该尽可能减小金属线末端的尺寸.

3 传输损耗

由于纳米金属线可以将THz 波的焦斑聚集到纳米量级. 但纳米尺度的焦斑究竟包含多少THz 能量?能否被探测到?需要知道纳米聚焦时THz SPPs强度的变化. 下面讨论利用锥形金属线进行纳米聚焦时，THz SPPs 强度的变化.

THz SPPs 在金属线上传输时，由式(10)可知，传输损耗系数为

可见，对于锥形金属线，不同传输位置的损耗系数不同，所以难以给出总体传输损耗的解析表达式.但是可以考虑把锥形金属线分成多个小段，认为在每一个小段中，传输损耗系数变化不大，因此可以把它看做常数，利用式(9)，分别计算每一段的传输损耗，然后把所有的损耗累加起来，就可得到锥形金属线的总体传输损耗. 基于该方法，计算了不同结构锥形纳米金属线THz 波传输时的强度变化.对于前端半径为100 nm，末端半径为1 nm，长度分别为1、10 和100 μm 的锥形金属线，其THz SPPs 传输时的强度变化如图3.

图3 THz SPPs 随传输距离的变化Fig.3 The intensity of THz SPPs versus propagating distance

由图3 可知，锥形金属线的长度越长，损耗越大. 当金属线长度为1 μm 时，能量损耗小于1%;当金属线长度为10 μm 时，能量损耗约为6%;当金属线长度为100 μm 时，能量损耗约为47%. 因此，虽然纳米金属线上THz SPPs 的传输损耗系数较大，但只要金属线长度小于100 μm，金属线前端THz SPPs 的能量大部分都可以传到末端，这样便于在末端对纳米尺度的THz SPPs 进行探测.

结 语

基于锥形金属线THz SPPs 传输理论，研究锥形金属线上THz 波的传输特性. 计算传输过程中横截面上的场分布，得到环形焦斑宽度约为金属线半径的2.4 倍. 提出求解锥形金属线上THz SPPs 传输强度变化的方法，研究不同结构金属线上THz SPPs强度随传输距离增加的变化规律，结果表明，虽然纳米金属线上THz SPPs 的传输损耗系数较大，但只要金属线长度不是很长，那么，金属线前端THz SPPs 的能量大部分都可以传到末端，从而使金属线末端有足够的THz 能量可以探测.

/References:

［1］ Wang K，Mittleman D M. Metal wires for terahertz waveguiding ［J］. Nature，2004，432(7015):376-379.

［2］LIU Sheng-gang. Recent development of terahertz science and technology ［J］. China Basic Science，2006，8(1):7-12.(in Chinese)刘盛纲. 太赫兹科学技术的新发展［J］. 中国基础科学，2006，8(1):7-12.

［3］SU Hong，ZHOU Hang，CHEN Qiong-zhou，et al. Multifrequency terahertz generation in a customed aperiodically poled lithium niobate ［J］. Journal of Shenzhen University Science and Engineering，2009，26(3):268-271.

［4］YANG Jun，RUAN Shuang-chen，ZHANG Min，et al.Experimental research on real-time continuous-wave terahertz imaging for mail inspection application ［J］. Journal of Shenzhen University Science and Engineering，2008，25(3):261-264.(in Chinese)杨 珺，阮双琛，张 敏，等. 实时连续太赫兹波成像在邮件检测方面的应用［J］. 深圳大学学报理工版，2008，25(3):261-264.

［5］Maier S A，Andrews S R，Martin-Moreno L，et al. Terahertz surface plasmon-polariton propagation and focusing on periodically corrugated metal wires ［J］. Physical Review Letters，2006，97(17):176805-1-176805-4.

［6］ LIANG Hua-wei，RUAN Shuang-chen，ZHANG Min.Terahertz surface wave propagation and focusing on conical metal wires ［J］. Optics Express，2008，16 (22):18241-18248.

［7］Astley V，Mendis R，Mittleman D M. Characterization of terahertz field confinement at the end of a tapered metal wire waveguide ［J］. Applied Physics Letters，2009，95(3):031104-1-031104-3.

［8］Awad M，Nagel M，Kurz H. Tapered sommerfeld wire terahertz near-field imaging ［J］，Applied Physics Letters，2009，94(5):051107-1-051107-3.

［9］LIANG Hua-wei，RUAN Shuang-chen，ZHANG Min，et al. Nanofocusing of terahertz wave on conical metal wire waveguides ［J］. Optics Communications，2010，283(2):262-264.

［10］YANG Jie，CAO Qin，ZHOU Chang-he. Theory for terahertz plasmons of metallic nanowires with sub-skin-depth diameters ［J］. Optics Express，2010，18(18):18550-18557.

［11］HE Xiao-yong. Investigation of terahertz surface waves of a metallic nanowire ［J］. Journal of the Optical Society of America B，2010，27(11):2298-2303.

［12］Goubau G. Surface waves and their application to transmission lines ［J］. Journal of Applied Physics，1950，21(11):1119-1128.

［13］King M J，Wiltse J C. Surface-wave propagation on coated and uncoated metal wires at millimeter wavelengths ［J］.IEEE Transactions on Antennas and Propagation，1962，10(3):246-254.

［14］Cao Q，Jahns J. Azimuthally polarized surface plasmons as effective terahertz waveguides ［J］. Optics Express，2005，13(2):511-518.