复射影空间中凯勒子流形的逐点拼挤问题

夏 霖

（1.浙江大学理学院，浙江杭州 310027；2.杭州第十四中学，浙江杭州 310006）

复射影空间中凯勒子流形的逐点拼挤问题

夏 霖1，2

（1.浙江大学理学院，浙江杭州 310027；2.杭州第十四中学，浙江杭州 310006）

研究了复射影空间中的完备凯勒子流形，利用活动标架法得到了和Ogiue的猜想相关的复射影空间中全测地子流形的部分拼挤结果.

复射影空间；子流形；拼挤问题；Ogiue猜想

0 引 言

设CPn＋p为具有常全纯截面曲率1的n＋p维复射影空间，Mn为CPn＋p中的n维完备凯勒子流形.Ogiue［1］曾有过以下猜想：

2）如果K＞0且p＜n（n＋1）/2，那么Mn为CPn＋p中的全测地子流形.

3）如果S＞（n/2）g，那么Mn为CPn＋p中的全测地子流形.

4）如果ρ＞n2，那么Mn为CPn＋p中的全测地子流形.

这里H，K，S，ρ，g分别表示Mn的全纯截曲率、截曲率、Ricci曲率、数量曲率和CPn＋p在M上自然诱导的凯勒度量.

对猜想1），当p＝1时，Ogiue在［1］中给出了证明.对一般的情形，Ros［2］已成功证明.

对猜想3），Ogiue在［1］中也给出了完整的证明.

对猜想2），Ogiue在［1］中给出了部分结果：

定理A 设Mn为浸入到CPn＋1中的完备凯勒超曲面，如果n≥4，K＞0，那么Mn为全测地子流形.

1976年，Ogiue在［3］中给出了进一步的结果：

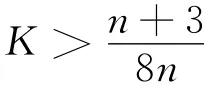
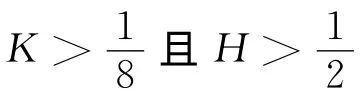
Ros和Verstraelen在［4］中将定理C的结果改进到：

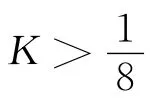
之后，盛为民［5］把定理A的条件改进到n≥2，得到同样的结论.

沈一兵［6］得到了如下结果：

定理E 设Mn为浸入到CPn＋p中的n维（n≥2）紧致凯勒子流形，如果K＞0，p＜n，那么Mn为全测地子流形.

笔者运用了类似于［1］中的方法得到了以下结果：

定理1 设Mn（n≥4）为CPn＋p中具平坦法丛的n维紧致凯勒子流形，如果K＞0，p＜n（n＋1）/2，那么Mn为全测地子流形.

进一步，得到：

定理2 设Mn（n＞4）为CPn＋p中具平坦法丛的n维紧致凯勒子流形，如果K＞0，那么Mn为全测地子流形.

对猜想4），在［1］中有如下定理：

定理F 设Mn为浸入到CPn＋p中的n维紧致凯勒子流形，如果ρ＞n（n＋1）－（n＋2）/3，那么Mn为全测地子流形.

注意到取n＝1的情形，就是猜想4）在Mn为紧致条件下的结论.

杜柏杨等［7］对上述定理作了推广，得到：

定理G 设Mn为浸入到CPn＋p中的n维完备凯勒子流形，如果ρ＞n（n＋1）－（n＋2）/3，那么Mn为全测地子流形.

此外当Mn的全纯截曲率和数量曲率满足一定条件时，笔者得到如下结果：

定理3 设Mn为浸入到CPn＋1中的完备凯勒超曲面，如果H≥δ＞（1－n）/2，ρ＞n2－4δ＋2，那么Mn为全测地超曲面.

1 基本公式与符号

设CPn＋p为具有常全纯截面曲率1的n＋p维复射影空间，Mn为CPn＋p中的n维Kaehler子流形，分别表示CPn＋p的复结构和凯勒度量表示CPn＋p关于的协变微分，以J，g，▽分别表示CPn＋p在Mn上自然诱导的复结构、Kaehler度量和协变微分，则Mn到CPn＋p的浸入的第二基本形式σ由下式给出：

且满足

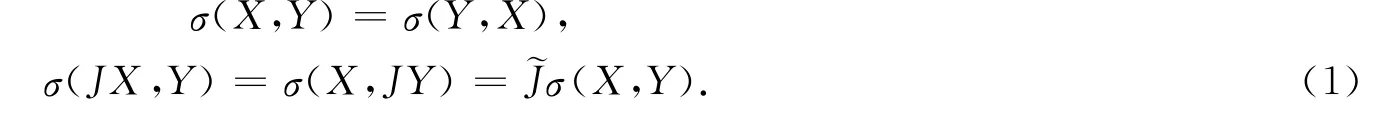
在CPn＋p上选取局部正交标架场

使得限制在Mn上，e1，…，en，e1＊，…，en＊切于Mn.对指标作如下约定：

设g（AλX，Y）＝~g（σ（X，Y），eλ），或者σ（X，Y）＝∑g（AλX，Y）eλ，则A~1，…，A~p，A~1＊，…，A~p＊都是对称线性变换.由（1）易得

于是

即Mn是CPn＋p的极小子流形.

设｛ωI｝为其对偶标架场，限制在Mn上，有

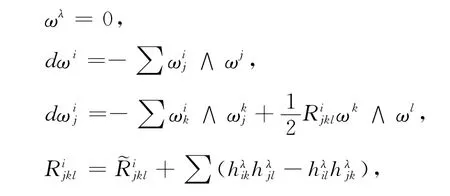
这里

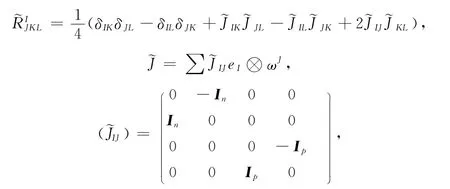
其中Is是s阶单位矩阵.Mn的数量曲率为

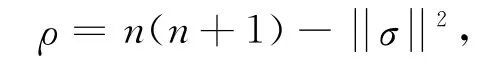
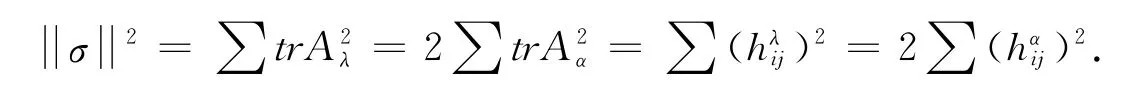
Mn的截面曲率

其中X，Y是正交向量.

Mn的全纯截面曲率为

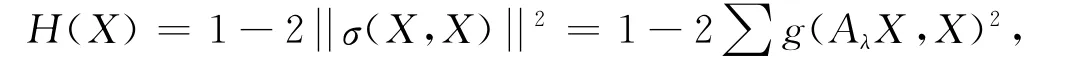
其中X是单位向量.

2 主要结果及其证明

对于定理1，2，3的证明，首先引进如下：

引理1［1］设Mn为浸入到CPn＋1中的完备凯勒超曲面，如果对某些常数δ，H≥δ＞（1－n）/2，则Mn紧致.

引理2［1］设Mn为浸入到CPn＋p中的n维完备凯勒子流形，则

其中Δ表示Laplacian，▽′表示协变微分.

引理3［1］条件同引理2，有

引理4［1］设Mn为浸入到CPn＋p中的完备凯勒子流形，如果

1）K＞0，

2）ρ为常数，

3）p＜n（n＋1）/2，

那么Mn为全测地子流形.

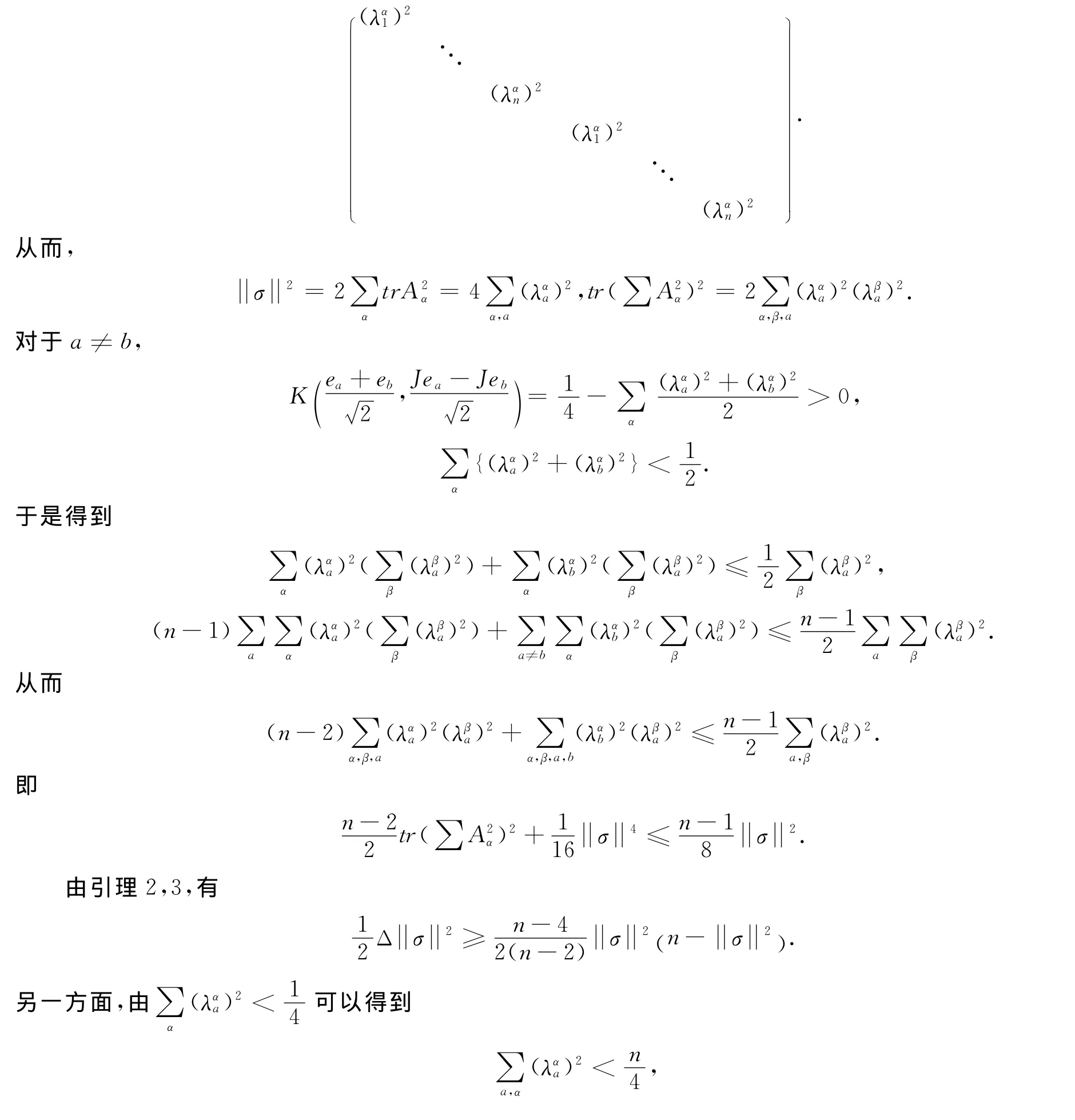
定理1的证明 因为Mn具有平坦法丛，所以在Mn的每一点x处，可以选择Tx（M）的一组正交基e1，…，en，Je1，…，Jen使得矩阵A2α具有以下形式：

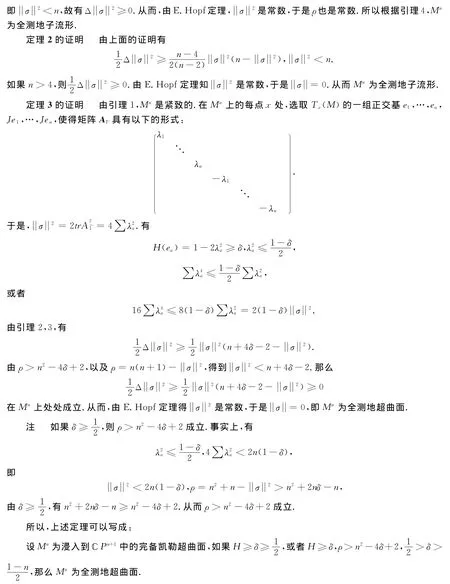
导师许洪伟教授对本文的写作予以了悉心指导，谨致谢意！

［1］Ogiue K.Differential geometry of Kaehler submanifolds［J］.Advance in Math，1974，13：73－114.

［2］Ros A.Positively curved Kaehler submanifolds［J］.Proc Amer Math Soc，1985，93：329－331.

［3］Ogiue K.Positively curved complex submanifolds immersed in a complex projective space［J］.J Differential Geomtry，1976，11：613－615.

［4］Ros A，Verstraelen L.On a conjecture of K.Ogiue［J］.J Differential Geometry，1984，19：561－566.

［5］Sheng Weimin.Kaehler hypersurfaces with positive sectional curvature in a complex projective space［J］.Chinese Ann Math，1994，15B：69－74.

［6］Shen Yibing.On compact Kaehler submanifolds inCPn＋pwith nonegative sectional curvature［J］.Proc Amer Math Soc，1995，123：3507－3512.

［7］杜柏杨，龚永洪.CPn＋p（1）中的完备Kaehler子流形［J］.四川师范大学学报：自然科学版，2001：24（1）：12－14.

Pointwise Pinching Problems of Kaehler Submanifold in Complex Projective Space

XIA Lin1，2

（1.College of Science，Zhejiang University，Hangzhou 310027，China；2.Hangzhou No.14Middle School，Hangzhou 310006，China）

This paper studied the complete Kaehler submanifold in complex projective space，and obtained some pinching results related to Ogiue's conjectures about the totally geodesic submanifold in complex projective space by the moving frame method.

complex projective space；submanifold；pinching problem；Ogiue's conjectures

O186.16 MSC2010：53C20

A

1674－232X（2012）06－0528－06

10.3969/j.issn.1674－232X.2012.06.011

2012－05－20

夏 霖（1982—），女，硕士，主要从事微分几何研究.E－mail：55871088＠qq.com