BMM-ESD 模拟器有源电路的模型构建*
张国红 ,吕红萍,汪金山
(1.金华市教育局教研室,浙江 金华321017;2.金华职业技术学院,浙江 金华321007;3.浙江师范大学数理信息学院,浙江 金华321004)
静电放电是一个复杂多变的过程,为了定量研究静电放电问题,人们建立了相应的多种电路模型,其中以BMM-ESD 模型最为典型[1]。BMM 是Body Machine Model 的缩写,即人体-金属模型,ESD 是英文Electro Statie Discharge 的缩写,即静电放电。
人体-金属模型静电放电(BMM-ESD)模拟器在电子工业领域应用广泛,常被用于电子器件和设备的静电敏感度测试。由于静电放电是一种高电位、强电场和瞬时大电流的脉冲,目前的BMM-ESD模拟器电路主要由电感、电阻、电容等无源器件组成,即为RLC 无源电路,这种电路简单可靠,但由于实际的电感L 在线性和集成方面存在困难等诸多问题,本文尝试用线性放大电路来构建一个能产生与RLC 电路有同样效果的BMM-ESD 模拟器,即构建一个能够产生微分方程解的电路结构,用来解决线性齐次微分方程的电路实现问题。
1 BMM-ESD 模拟器无源电路模型
1.1 一个六阶BMM-ESD 模拟器无源LC 电路
由于人体的等效参量具有复杂性,电路建模须考虑人体及手、前臂等部位的分布参数,综合BMM-ESD的自身特征,需要构建多阶的BMM-ESD 电路模型,以较好地描述BMM-ESD 电流的寄生振荡。本文以一个六阶的BMM-ESD 模拟器无源LC 电路为设计基础,来构建对应的无源电路,如图1 所示。其中,R1,L1,C1分别为人体电阻、人体电感和人体电容,Cp1、Cp、Cp2分别为人体寄生电容、放电气隙寄生电容以及金属物的分布电容,R3、R2分别为放电气隙电阻和金属物(对地)电阻,i(t)为BMM-ESD 电流[2-3]。
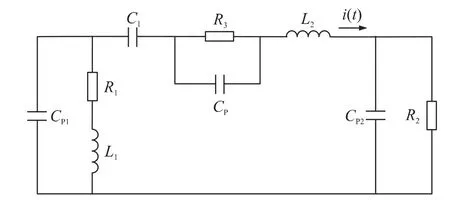
图1 六阶BMM-ESD 模拟器无源LC 电路
给出两组参量,如表1 所示。

表1 六阶BMM-ESD 模拟器无源LC 电路参量
1.2 BMM-ESD 电流波形仿真
假设依据参量组合1 取值,在Multisim 软件作仿真电路,仿真接线图如图2 所示。考虑测量的是输出电流脉冲,所以串接一个1 欧姆的电阻R4,示波器测到的是电阻R4两端的电压。
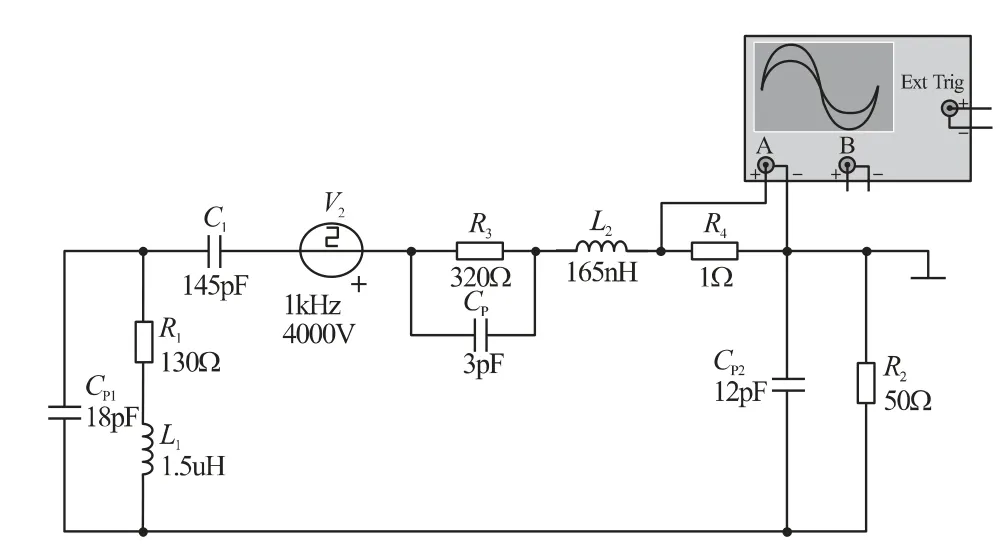
图2 六阶BMM-ESD 模拟器无源LC 电路接线图
其仿真结果如图3 所示。
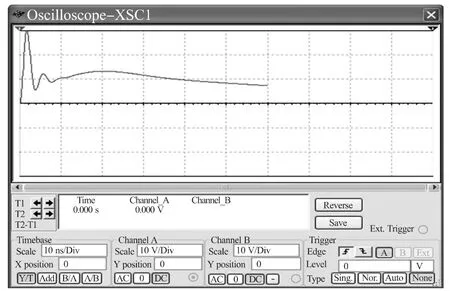
图3 六阶BMM-ESD 模拟器无源LC 电路仿真结果
图3中可以看出,以组合1 为例的电流仿真波形与IEC61000-4-2 标准波形一致性好[4],通过读数,4 个基本指标(上升时间tr、峰值电流Ip、30 ns 时电流值I-30 和60 ns 时电流值I-60)均吻合IEC61000-4-2 标准,通过数学计算也证明,组合1 与组合2 参数对应电流波形的4 个基本指标的计算结果均吻合IEC61000-4-2 标准。
2 BMM-ESD 模拟器有源电路模型的构建
2.1 BMM-ESD 模拟器有源电路设计[5-6]
根据图3 所示的无源BMM-ESD 模拟器电路,通过数学计算的方法,设计形成一个基于微分方程解的有源BMM-ESD 模拟器电路,并在Matlab 软件平台做仿真实验。计算与设计过程如下[7]:
对图3 作拉普拉斯变换,得到复频域电路模型,如图4 所示。
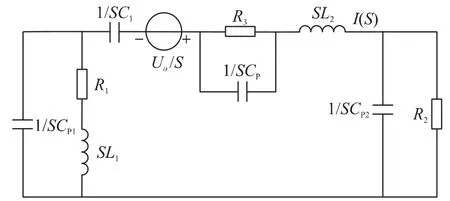
图4 六阶BMM-ESD 模拟器复频域电路
依据Kirchhoff 定律可推导出:
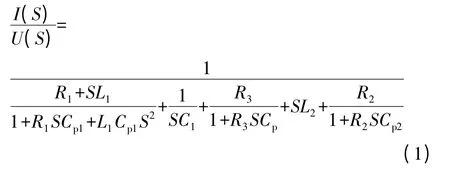
把式(1)转化成标准形式得:
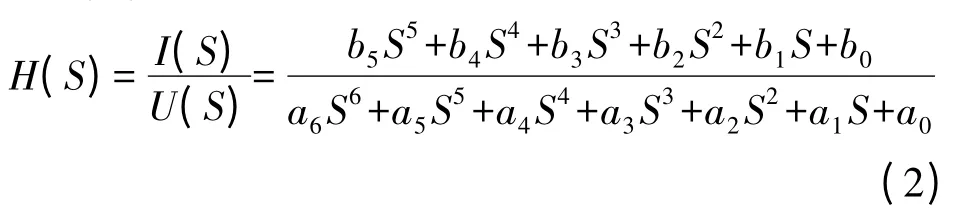
对式(1)作通分与变换后可得到与式(2)相一致的标准形式(由于该标准形式展开后的分子、分母较长,完整的表达式不具体列出)。
通过计算,可解出式(2)的各系数为:
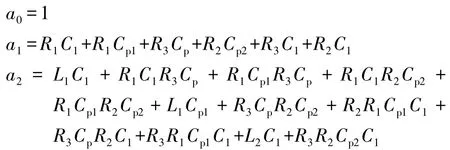

对式(2)作移相,并作拉普拉斯反变换可得到:

对式(3)两边对时间积分6 次可得:

根据表(1)给出的参量组合1 可算出:

根据式(4)积分方程,可形成以积分器为电路主体的有源BMM-ESD 模拟器电路[8-9],在Matlab软件上的仿真接线图如图5 所示。
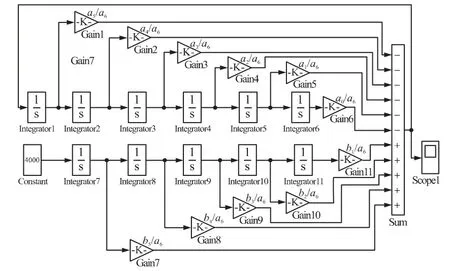
图5 六阶BMM-ESD 模拟器有源电路模型
图5中Integrator1 ~Integrator11 为积分器,共11 个;Gain1 ~Gain11 是线性放大器,共11 个;Sum为加法器;Constant 为固定电源;Scope 为示波器。
式(4)积分方程的各项系数大小由图5 所示对应的线性放大器的放大倍数和积分器系数的乘积决定,假设积分器运用如图6 所示单元电路。
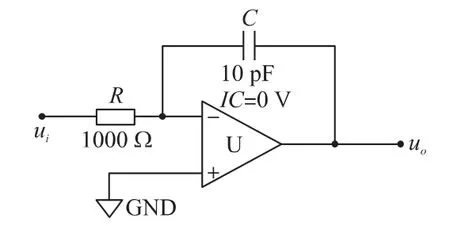
图6 单元积分电路
即取输入电阻R=1 kΩ,反馈电容C=10 pF,则有:
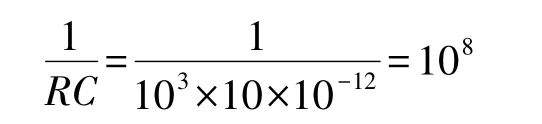
则对应的线性放大电路电压放大倍数为:
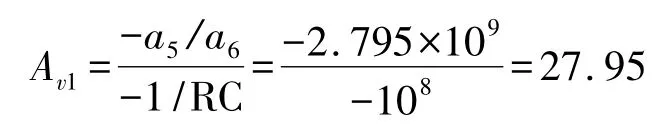
以此类推,可计算各放大器的放大倍数设置值如表2 所示。
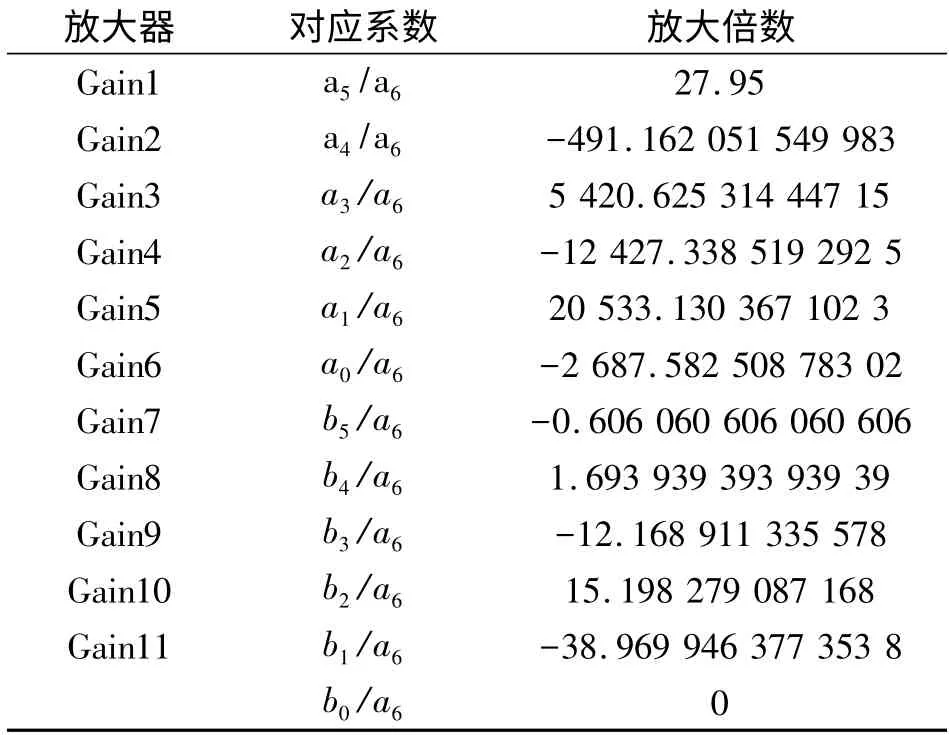
表2 六阶BMM-ESD 模拟器有源电路模型放大器参数
2.2 BMM-ESD 模拟器有源电路电流波形仿真
可以说,图5 所示电路已经给我们建立了一个六阶BMM-ESD 模拟器有源电路模型,在Matlab 软件平台上可以验证电路设计的准确性[10],及相关数据分析。其仿真结果如图7 所示。
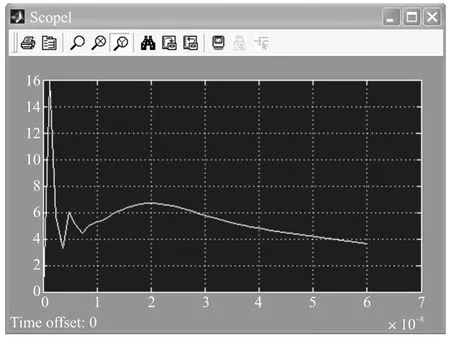
图7 六阶BMM-ESD 模拟器有源电路电流仿真结果
从图7 波形看出,该六阶BMM-ESD 模拟器有源电路的电流仿真波形与图3 所示六阶BMM-ESD模拟器无源LC 电路的仿真结果完全吻合,验证了图5 所示电路模型的正确性与可行性。
3 结束语
以六阶BMM-ESD 模拟器无源LC 电路为例,通过求微分方程解的方法,设计形成了一个以积分器、线性放大器为主体的BMM-ESD 模拟器有源电路模型,这种设计思路具有普遍意义。但是,要真正构建形成实用的BMM-ESD 模拟器有源电路,还需要克服电路延时及对元件参数的高要求等问题。
[1] Bendjamin J,Thottappillil R,Scuka V. Time Varying Magnetic Fields Generated by Human Metal(ESD)Electrostatic Discharges[J].Journal of Electrostatics,1999(46):259-269.
[2] 汪金山.基于4 阶HMM-ESD 电路的电流解析式[J].仪器仪表学报,2009,30(6):590-592.
[3] 周峰,徐丹,黄久生,等.一种新的BMM-ESD 电流解析式计算方法[J].高电压技术,2007,33(5):26-28.
[4] IEC 61000-4-2.Electromagnetic Compatibility(EMC)-Part 4-2:Testing and Measurement Techniques-Electrostatic Discharge Immunity Test[S].2002.
[5] 许永生,陶永刚,洪亮,等.一种带封装及ESD 保护电路的低噪声放大器设计[J].电子器件,2006,29(3):691-696.
[6] 朱志炜,郝跃,马晓华.一种改进的片内ESD 保护电路仿真设计方法[J].电子器件,2007,30(4):1160-1163.
[7] 郑君里,应启珩,杨为理.信号与系统(上册)[M]. 北京:高等教育出版社,2010:28-31.
[8] 吴秀华,赵磊.温室温湿度非线性控制器的设计与MATLAB 仿真研究[J].沈阳农业大学学报,2011,42(1):121-124.
[9] Tanaka H,Fujiwara O,Yamanaka Y,et al. A Circuit Approach to Simulate Discharge Current Injected in Contact wit h an ESD-Gun[C]//Elect Romagnetic Compatibility,2002 3rd International Symposium on 21-24 May 2002,486-489.
[10] 李林,董林玺.基于Matlab 的交流感应电机矢量控制系统研究[J].电子器件,2010,33(5):618-621.

