一种应用于45 nm MOSFET 电学仿真的版图相关的PSP 应力模型*

汪明娟，李 曦，张孟迪，任 铮，，胡少坚，石艳玲*

(1.华东师范大学电子工程系，上海200241;2.上海集成电路研发中心，上海201210)

随着半导体器件特征尺寸日益减小并进入纳米级别，版图面积不断缩小，各种物理效应变得越来越显著，使MOSFET 的阈值电压发生漂移，载流子的迁移率发生变化，进而改变了器件的输出特性［1－4］。

在纳米级的电路中，应力技术已成为提高CMOS性能不可缺少的一部分。通过DSL(Dual Stress Liner)技术和SMT(Stress Memorization Technique)技术获取高的饱和电流［5－6］，采用Embedded SiGe 技术［7－8］增加沟道应力，从而提高载流子的迁移率。以及STI(Shallow Trench Isolation)［9］无意识的引入应力。但是同时这些技术的引入，让版图结构对器件的影响越来越显著，我们从版图布局来考虑各种应力对器件性能的影响，以此建立版图相关的应力模型［10－12］。

至今已经提出了多种版图相关的应力模型，如STI引起的机械应力模型［13］、WPE(Well－Edge Proximity Effect)模型［14］、由于接触孔带来的刻蚀终止层所引起的应力模型［15］等等。在现有文献中的应力模型中，没有单独地分析多晶硅栅极相关应力效应的模型。

本文描述的版图相关的应力模型采用的是45 nm 工艺器件，考虑了栅极PC 相关的版图效应:相邻PC 的间距、dummy PC 个数，并且考虑不同l/w 尺寸的器件下PC 间距作用，有一定的扩展性。根据以上版图效应，绘制不同尺寸的器件，对器件进行测试和计算得到Idlin、Idsat、Vtlin、Vtsat随着版图参数变化的曲线图。根据数据变化趋势，提出一个经验PSP 模型。该应力模型，是在原有的PSP 模型中，引入版图参数和相应的影响系数，并将这些参数和模型公式以子电路的形式引入到PSP SPICE 模型平台中去，重新定义PSP 模型中的两个基本参数μ0和VFB0。该模型得到了实际测量数据的验证，很好地拟合了测量数据的趋势，保证电路的仿真更加准确。

PSP 模型是目前业界对22 nm ～130 nm 标准工艺MOSFET 进行建模时新型模型。PSP 模型是一种表面电势模型(Surface－Potential)。与其他可选模型比较，表面势模型更接近晶体管实际行为，并能够就IC 性能做出更好的预测。因此考虑PSP 模型，显得更加准确，有物理意义。

1 建立模型

研究发现可以用两个主要机制来概括应力对器件性能的影响:一个是和迁移率相关;另一个是和阈值电压相关。通过改变原有PSP 模型的两个基本参数μ0和VFB0，建立一个经验模型。

图1 为本文描述的MOSFET 应力模型的版图示意图。本文考虑了以下版图效应:相邻PC 的间距pc，dummy PC 个数pcdum。

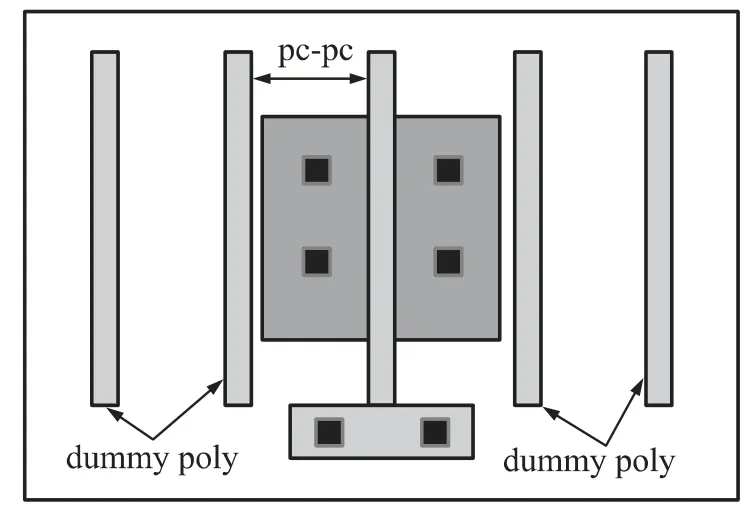
图1 应力模型版图示意图

1.1 迁移率相关方程

模型介绍的第1 种机制是根据不同的版图，调整μ0，下面是对应的方程:

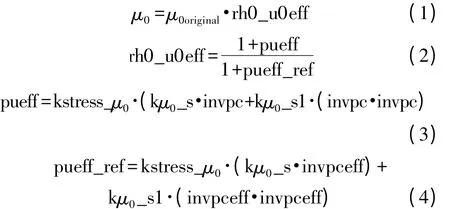
其中，kμ0_s、kμ0_s1 分别表征是pc、pcdum 对迁移率影响程度的一次系数和二次系数，kstress_μ0是表征器件沟道长度l 和沟道宽度w 对迁移率的调制因子的参数。

1.2 阈值电压相关方程

第2 种机制是根据不同的版图，调整Vth0。下面是相应的方程:

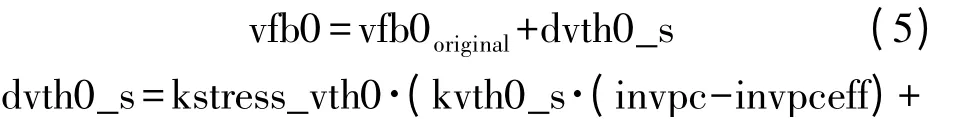
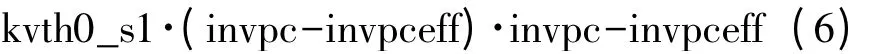
其中，kvth0_s、kvth0_s1 分别表征是pc、pcdum 对阈值电压影响程度的一次系数和二次系数，kstress_vth0 是表征器件沟道长度l 和沟道宽度w 对阈值电压的调制因子的。

1.3 中间变量。

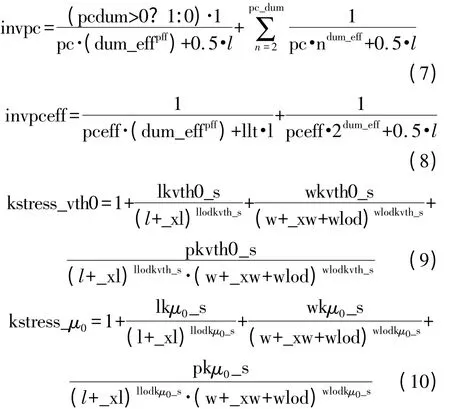
其中，invpc、invpceff、kstress_μ0和kstress_vth0 分别是中间变量。invpc 和invpceff 分别是对实际版图参量和有效值做了倒数运算。其中，pc、pcdum 是模型参数，pceff、dum_eff 是相应的有效值。

2 实验结果及讨论

本文中所采用的目标器件是l=0.04 μm、w=0.5 μm 的nMSOFET。分别在Vds=0.1 V、1.1 V 的情况下，对器件施加扫描电压Vbs、Vgs，得到曲线Id_Vgs_Vbs;以及在Vbs=0、1.1 V 的情况下，对器件施加扫描电压Vds、Vgs，得到曲线Id_Vds_Vgs。然后从四张曲线中，分别计算出Idlin、Idsat、Vtlin、Vtsat的值。根据测量计算得到的结果，分别得到Idlin、Idsat、Vtlin、Vtsat随着版图参数变化的曲线图，如图2 和图3 所示。图中，实线是PSP 模型的仿真值，点是实际测量的值。

图中，x 轴分别是上述版图参数，y 轴分别是Idlin、Idsat、Vtlin、Vtsat。以目标器件为准，器件的Idlin、Idsat取其相对变化量，所以结果是百分比;Vtlin、Vtsat取其变化量，单位是mV。

2.1 多晶硅栅极间距pc

随着pc 的增加，分布在晶体管沟道的应力就会相应的增加，使得载流子的迁移率增加。所以和载流子迁移率相关的电流都会有所增加，阈值电压会相应的有所降低。图2 是Idlin、Idsat、Vtlin、Vtsat随着pc的变化曲线曲线。

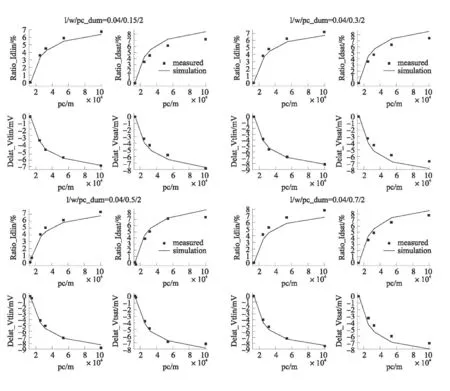
图2 Idlin、Idsat、Vtlin、Vtsat 随着pc 的变化曲线

本文中，分别提供四组l/w，l/w=0.04/0.15、0.04/0.3、0.04/0.5、0.04/0.7。每一组l/w 下，pc分别取0.14、0.25、0.32、0.54、1 等5 个值，并且取pc=0.14 作为目标器件。由图可知:对于相同l/w的器件，随着pc 的增加，器件的Idlin、Idsat的值逐渐增加，Vtlin、Vtsat的值逐渐降低。其中Idlin和Idsat最大相对变化量分别是6.8%、7.17%，Vtlin、Vtsat最大变化量分别是7.88 mV、7.77 mV。并且由图中可以观察到，对于相同的pc 的器件，随着l/w 的增加，器件的Idlin、Idsat的值逐渐降低，Vtlin、Vtsat的值逐渐增加。

2.2 dummy 多晶硅的个数pc_dum

Dummy poly 对于晶体管的影响主要原因是dummy 的个数会改变应力在晶体管中的分布。随着dummy poly 个数的增加，分布在晶体管内部的应力会越来越弱，相当于是应力被多出来的dummy poly 给减弱了，所以晶体管沟道的应力减弱了，载流子的迁移率也减小了。从侧面也可以看出:第一根dummy 对晶体管的影响比较明显，而越远离栅极的dummy 对晶体管的影响会越来越小。

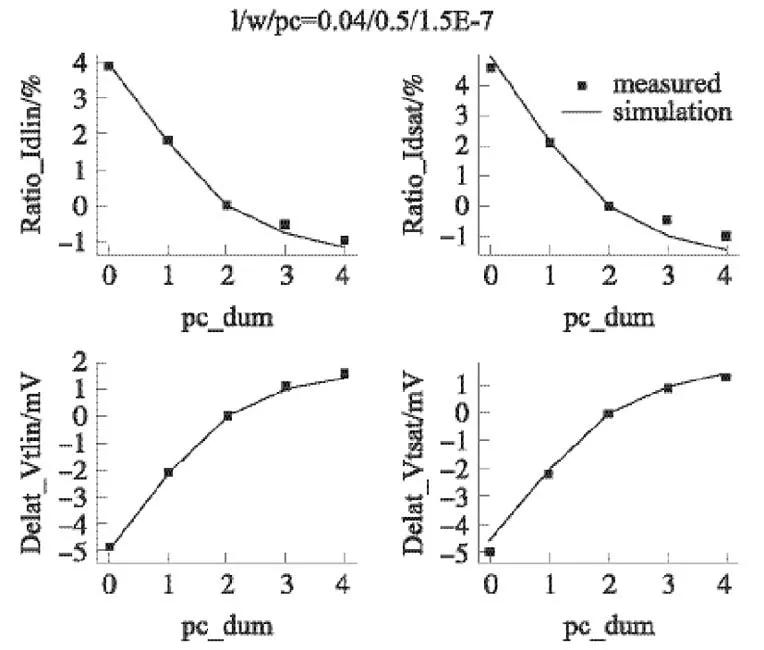
图3 Idlin、Idsat、Vtlin、Vtsat 随着pc_dum 的变化曲线

图3 所示的是Idlin、Idsat、Vtlin、Vtsat随着pc_dum 的变化曲线。器件的l/w=0.04/0.5。pc_dum 分别取0、1、2、3、4 等5 个值，并且取pc_dum=2 作为目标器件。由图可知:随着pc_dum 的增加，Idlin、Idsat的值逐渐降低，Vtlin、Vtsat的值逐渐增加。其中Idlin和Idsat最大相对变化量分别是3.9%、4.6%，Vtlin、Vtsat最大变化量分别是4.9 mV、5 mV。

由以上一组组曲线可以看出，Idlin、Idsat与Vtlin、Vtsat的变化趋势刚好相反，并且随着参数的增加，Idlin、Idsat、Vtlin、Vtsat的变化趋势都趋于平缓，呈水平收敛状。

3 总结

本文提出了一种应用于45nm MOSFET 电学仿真的版图相关的PSP 应力模型。该模型考虑了多晶硅栅极相关的两种版图效应:相邻PC(多晶硅栅)的间距、dummy PC 个数，同时还包括了不同l/w尺寸的器件下PC 间距的影响，有一定的扩展性。该模型很好的拟合了测量数据，得到了测量数据的验证。随着半导体器件尺寸日益减小，器件结构越来越复杂，本文提出的模型对于电路设计来说非常有帮助。

［1］ Bianehi R A，Bouche C，Roux－dit－Buisson O.Accurate Modeling of Trench Isolation Induced Mechanical Stress Effect on MOSFET Electrical Performance［J］.IEDM，2002:117－120.

［2］ Tsuno H，Anzai H，Matsumura M，et al. Advanced Analysis and Modeling of MOSFET Characteristic Fluctuation Caused by Layout Variation［J］.VLSI，2007:204－205.

［3］ Moroz M，Eneman G，Verheyen P，et al. The Impact of Layout on Stress－Enhanced Transistor Performance［J］.SISPAD，2005:143－146.

［4］ Aikawa H，Morifuji E，Sanuki T，et al.Variability Aware Modeling and Characterization in Standard Cell in 45 nm CMOS with Stress Enhancement Technique［J］.IEEE VLSI，2008:90－91.

［5］ Ito S，Namba H，Yamaguchi K，et al. Mechanical Stress Effect of Etch－Stop Nitride and Its Impact on Deep Submicron Transistor Design［J］.IEDM，2000:247－250.

［6］ Grudowski P，Adams V，Xiang－Zheng Bo，et al.1－D and 2－D Geometry Effects in Uniaxially－Strained Dual Etch Stop Layer Stressor Integrations［J］.VLSI，2006:62－63.

［7］ Thompson S E，Armstrong M，Auth M，et al.A 90－nm Logic Technology Featuring Strained－Silicon［J］.IEEE Trans.Electron Devices，2004，51(11):1790－1797.

［8］ Thompson S E，Su G，Choi Y S，et al. Uniaxial－Process－Induced Strained－Si:Extending the CMOS Roadmap［J］.IEEE Trans.Electron Devices，2006，53(5):1010－1020.

［9］ Kahng A B，Sharma P，Topaloglu R O. Exploiting STI Stress for Performance［J］.ICCAD，2007:83－90.

［10］ Tanaka T，Satoh A，Yamaji M，et al.Fully Considered Layout Variation Analysis and Compact Modeling of MOSFETs and Its Application to Circuit Simulation［J］.IEEE Conf.on Microelectronic Test Structures，2008:223－227.

［11］ Wang Chi－Chao，Zhao Wei，Liu F，et al.Modeling of Layout－Dependent Stress Effect in CMOS Design［J］.ICCAD，2009:513－520.

［12］ Aikawa H，Sanuki T，Sakata A，et al. Compact Model for Layout Dependence Variability［J］.IEDM，2009:1－4.

［13］ Su Ke－Wei，Sheu Yi－Ming，Lin Chung－Kai，et al.A Scaleable Model for STI Mechanical Stress Effect on Layout Dependence of MOS Electrical Characteristics［J］.Custom Integrated Circuits Conf.，2003:245－248.

［14］ Sheu Y M，Su K W，Yang S J，et al.Modeling the Well－Edge Proximity Effect in Highly Scaled MOSFETs［J］. IEEE Custom Integrated Circuits Conf，2005:831－834.

［15］ Liebmann R，Nawaz N，Bach K H，et al.Efficient 2D Approximation for Layout－Dependence Relaxation of Etch Stop Liner Stress due to Contact Holes［J］.SISPAD，2006:173－175.