原子电荷计算方法的对比

卢 天 陈飞武

(北京科技大学化学与生物工程学院,北京100083)

原子电荷计算方法的对比

卢 天 陈飞武*

(北京科技大学化学与生物工程学院,北京100083)

原子电荷是对化学体系中电荷分布最简单、最直观的描述形式之一,在理论和实际应用中都有重要意义.本文介绍了12种重要的原子电荷计算方法的原理和特点,通过大量实例从不同角度比较了它们的优缺点.这些方法包括Mulliken、分子环境中的原子轨道(AOIM)、Hirshfeld、原子偶极矩校正的Hirshfeld布居(ADCH)、自然布居分析(NPA)、Merz-Kollmann(MK)、分子中的原子(AIM)、Merck分子力场94(MMFF94)、AM1-BCC、Gasteiger、电荷模型2(CM2)以及电荷均衡(QEq)方法.最后本文对如何在实际应用中选择合适的计算方法给出了建议.

原子电荷;计算化学;布居分析;电负性;静电势

1 引言

原子电荷,即位于原子中心的点电荷,是对化学体系中电荷分布最简单、最直观的描述方式之一.它有很多重要意义,比如帮助化学工作者研究原子在各种化学环境中的状态、1考察分子性质、2,3预测反应位点.4另外原子电荷模型在计算化学中也有很多实用价值,如作为分子描述符用于药物虚拟筛选、5在分子对接和分子动力学/蒙特卡罗模拟中描述静电作用、6在量子力学(QM)与分子力学(MM)结合计算中表现QM区域原子对MM区域原子的静电作用势.7在其它一些理论方法中也需要借助原子电荷,如Pipek-Mezey轨道定域化方法、8电荷自洽的紧束缚密度泛函方法(SCC-DFTB)、9Truhlar课题组开发的一系列溶剂模型(SM)10-13等.

原子电荷并不是可观测量,也没有客观、唯一的定义,因此获得原子电荷的方法多种多样.通过一些实验数据可以间接地考察原子电荷,14如通过分子的多极矩、红外光谱强度和频率、配体场分裂能、核磁共振(NMR)位移等,但是数据的获取相对不便,与原子电荷的对应关系存在较大经验性,也不能分析不稳定的体系和状态.计算化学的发展使原子电荷方便、快速、可靠的获得成为了可能.15-18自从1955年Mulliken电荷19-21被提出以来,迄今已有不下60种原子电荷计算方法被相继提出,近年仍有许多研究者在改进计算方法.

虽然在许多计算方法的原文和部分文献22-25中都对不同类型原子电荷进行了比较和讨论,但是涉及的方法并不全面,测试分子和测试内容缺乏统一性.因此,很有必要对较为重要的、文献中常涉及的原子电荷计算方法进行综合的比较,使它们的特点、优缺点能够清晰地展现,这将有助于在实际问题研究中选择适合的计算方法.我们选取Mulliken、分子环境中的原子轨道(AOIM)、26Hirshfeld、27原子偶极矩校正的Hirshfeld布居(ADCH)、28自然布居分析(NPA)、29Merz-Kollmann(MK)、30分子中的原子(AIM)、31Merck分子力场94(MMFF94)、32,33AM1-BCC、34,35Gasteiger、36电荷模型2(CM2)37和电荷均衡(QEq)38共12种方法.在文中将首先介绍这些方法的基本原理和特点,之后通过实际体系测试和比较它们的各方面性能,最后讨论计算量的大小,并给出方法选择上的建议.

2 各种原子电荷计算方法的原理和特点

2.1 Mulliken方法

Mulliken方法19-21是最古老的原子电荷计算方法.它的算法简单,计算量可忽略不计,几乎出现在所有量子化学软件中.首先考虑分子轨道波函数归一化条件(假设为实函数,后同)

r代表空间坐标.将分子轨道ϕi按以原子为中心的基函数χm展开

这里C代表系数矩阵.将式(2)代入式(1),积分后得

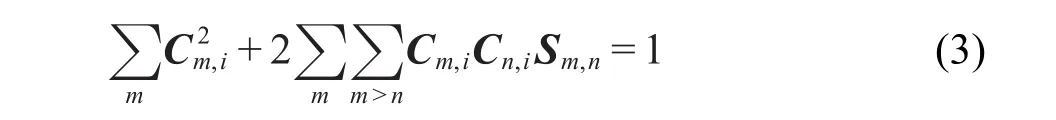
其中Sm,n=∫χm(r)χn(r)dr.上式中第一项可视为各个基函数对轨道独立贡献之和,称定域项;第二项是交叉项,体现了由于每一对基函数之间的耦合对轨道产生的联合贡献.Mulliken将分子轨道i中基函数m所占成分定义为

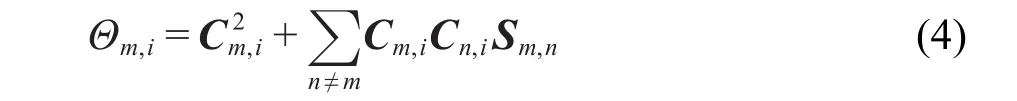
也就是说,定域项被完全划归到相应基函数,而交叉项被平分给对应的两个基函数.将所有轨道中属于相同原子的基函数的占据数加和就得到了原子占据数,并直接得到原子电荷

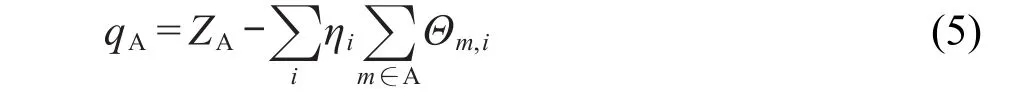
其中Z是原子核电荷数,η是轨道占据数.

Mulliken电荷存在一些严重问题:(1)交叉项平分的做法物理意义不严格,没有考虑到原子间的差异性;(2)基组依赖性非常大.尤其是使用大基组、含弥散函数基组的情况下问题更为明显.这主要是因为弥散函数延展范围大,容易破坏基组的平衡性,后有一些研究者提出了不同方法试图改进交叉项划分的不合理性,39-43其中也包括使用相对较多的Löwdin方法,39但是严重的基组依赖性却并没消除,也并未普及开来.

2.2 NPA方法

自然布居分析(NPA)29的关键是将带有随意性的原始基组(一般为扩展基)描述的波函数转化到物理意义清晰的正交极小基下描述,使基函数与原子轨道有明确对应关系,很大程度避免了基组不平衡性问题对结果的影响,也避免了划分交叉项的困难.

NPA的原理如下.首先根据原始基函数与原子的对应关系将单粒子密度矩阵中对应于各个原子的对角块依次提取并对角化,所得本征向量就是初自然原子轨道(PNAO),其本征值就是PNAO的占据数.根据占据数可将PNAO分为两类:(1)极小集轨道.它们拥有较高占据数,是对原子上的电子密度最主要、最紧凑的描述,与基态原子的内层和价层原子轨道一一对应.(2)里德堡集轨道.这是指PNAO中除极小集轨道之外的、电子占据数很少的轨道,它们对原子的电子密度的描述不起主要作用.随后对这些PNAO进行占据数权重的对称正交化(OWSO),使它们不仅在原子内正交也在原子间正交.相对于其它正交化方法,OWSO方法可以使有意义的极小集轨道变形尽量小,而允许意义不大的里德堡集轨道自由变化,物理意义更明确.PNAO在正交化后被称为自然原子轨道(NAO).以NAO为基重新构建体系单粒子密度矩阵,将对应于相应原子的矩阵对角元加和就得到了原子占据数.

值得一提的是,由于NPA是自然键轨道(NBO)方法44框架内的一个组成部分,而且NPA电荷通常由Weinhold等开发的NBO程序45计算,所以NPA电荷经常在文献中被称为NBO电荷.

2.3 AOIM方法

和NPA的出发点相近,黎乐民等26,46提出的分子环境中的原子轨道(AOIM)方法也是将原始扩展基下的波函数转化为极小基描述后再做布居分析. AOIM有两种不同的具体实现方法:

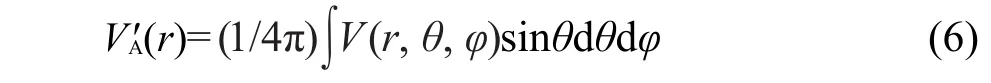
第一种方法46认为分子环境会使得原子轨道相对于原子在自由状态时收缩或扩张,分子环境的影响通过平均化的球对称有效外势来表达其中r,θ和φ是球坐标,球坐标系以原子A的原子核为中心,V是分子势场.在这样的有效势下解原子的径向薛定谔方程,所得波函数结合角度波函数就是分子环境下的原子轨道.实际求解时使用变分法,将计算分子时用的扩展基的径向函数作为变分函数,就得到了原先扩展基与新的极小基之间的变换关系.

第二种方法26利用Sanchez-Portal投影方法47,48将扩展基波函数投影到Slater极小基轨道(STO).设Löwdin正交化后的扩展基为φortho,系数矩阵为Cʹ;所期望的极小基在Löwdin正交化后为χortho,系数矩阵为Cʹ(mini),则变换关系为基函数的约化会导致基组完备性下降,从而使波函数信息丢失,衡量丢失量的参数为.它是STO的指数与方向的函数.为了最大程度避免因约化带来的基组不完备性增加,通过有限内存大尺度限制性优化(L-BFGS-B)方法最小化Δ就得到在分子环境下膨胀、收缩和旋转后的原子轨道.通过上述过程得到极小基下的系数矩阵后,就可以照常按照Mulliken方法计算原子电荷.下文中涉及的AOIM方法都特指第二种AOIM方法.

2.4 AIM方法

Bader的分子中的原子(AIM)方法31,49是典型的基于实空间划分的计算原子电荷的方法.AIM方法将电子密度零通量面定义为原子间的分界面,划分出的每个原子独立的空间被称为原子盆.在分界面上没有电子密度梯度线穿过,即满足Δρ(rʹ)·n(rʹ)=0,这里rʹ为原子界面上的任意点,n为界面上的单位法矢量,ρ是电子密度函数.这样的空间划分从量子力学角度来看理论意义明确,在每个原子盆内维里定理得到满足.对原子盆内电子密度积分并与核电荷求差值即得到原子电荷这里ΩA代表A原子盆.注意以AIM的划分,在特殊条件下可能会出现不含原子核的原子盆,被称为赝原子.例如锂金属的两个锂原子间就存在赝原子,这是由金属键所导致的.另外还可能出现一个盆内包含不止一个原子核的情况,如KrH+体系中Kr由于电子分布范围过广而淹没了氢.这些情况都无法使用AIM方法来计算原子电荷.

2.5 Hirshfeld方法

Hirshfeld电荷写为

其中

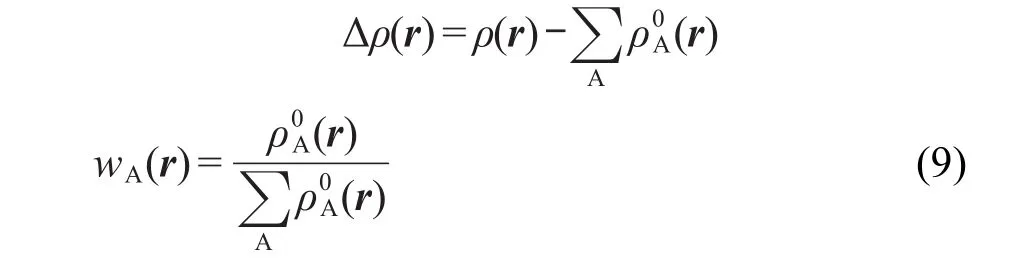
2.6 ADCH方法

Hirshfeld电荷数值普遍偏小,51而且偶极矩、静电势重现性比较差,25我们认为这主要是忽略了原子偶极矩所引起的.原子偶极矩可定义为

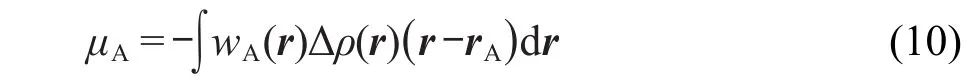
其中rA代表A原子核坐标.原子偶极矩是对原子空间内电子密度各向异性分布最重要的描述,它对分子可观测性质有直接贡献.然而式(8)的积分却相当于把原子空间内电子密度的分布球对称化了,完全掩盖了原子偶极矩的效应.因此提出了原子偶极矩校正的Hirshfeld布居(ADCH).28在这个方法中首先计算各个原子的Hirshfeld电荷及原子偶极矩,然后将每个原子偶极矩按下式展开成为周围原子的校正电荷

其中ΔqAB代表展开A原子偶极矩后对B原子产生的校正电荷.把所有原子偶极矩展开成校正电荷后,将校正电荷累加到原始Hirshfeld电荷上就得到了ADCH电荷.为了保证分子净电荷在校正过程中不变,展开任一原子A的偶极矩时需满足这个条件

同时,为了让原子偶极矩只展开到离当前原子较近的原子上,在实际计算时令式(11)和式(12)以拉格朗日乘子方式作为限制条件,使下式最小化来获得A原子对其它原子产生的校正电荷

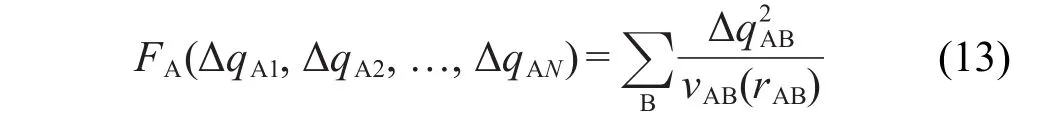
其中rAB是A、B原子间距离,N是总原子数,ν是依赖于原子间距离的函数.它呈倒S形状,当rAB由0变化到A、B原子范德华半径之和的过程中νAB由1变化为0.因此,在原子偶极矩展开时,离当前原子越近的原子越容易获得校正电荷,与当前原子无相互作用的原子(距离超过范德华半径和)的电荷不会受到影响.

2.7 MK方法

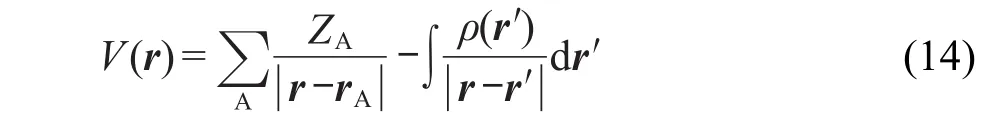
在化学体系中,静电势(ESP)由原子核电荷和电子密度两部分贡献构成对于离原子核较近的区域,总是由第一项主导,静电势数值为正,这是化学上不感兴趣的.而体系范德华表面以外的区域静电势可正可负,具有显著的化学意义,对于研究受体-配体结合方式、晶体堆叠方式,预测亲核/亲电反应位点,通过比较场分析(CoMFA)进行药物筛选等问题至关重要.若在分子范德华表面外侧一定范围内选取一批格点,通过最小二乘法令原子电荷在这些点产生的静电势

对式(14)计算的静电势拟合,就得到了拟合静电势电荷.拟合静电势电荷计算方法很多,主要差异在于格点位置的选取和拟合过程的细节.最常见的方法有Merz-Kollman(MK)方法、30静电势获得的电荷(CHELP)方法52和基于格点的CHELP(CHELPG)方法.53CHELPG电荷在三者中旋转不变性最好,而通过多极矩重现性分析发现MK电荷质量比CHELP和CHELPG略好,54因此本文选取MK电荷作为拟合静电势电荷的代表在后文中与其它类型电荷进行比较.

2.8 AM1-BCC方法

传统拟合静电势方法存在一些弊端,例如:(1)电荷对构象依赖性较大;(2)单一构象拟合的原子电荷不能体现原子的等价性,例如一氯丙烷中甲基的三个氢是化学等价的,但任何构象下拟合出来的这三个氢的电荷都不是全同的;(3)内部被包埋的原子电荷拟合不准确,这是由于这些原子距离拟合点过远所导致的.这三个问题使得拟合静电势电荷用于分子动力学模拟等问题中可能导致错误的结果.限制性静电势拟合(RESP)方法55可以很大程度解决这些弊端,它对内部原子在拟合时施加限制势以降低数值不稳定性,对等价原子在拟合时强制相等,并且将拟合分为两步或者多步以提高拟合质量.然而计算RESP电荷过程相对复杂,而且需要较为准确的量子化学方法计算静电势,用于大批量或者较大分子体系较为耗时.

AM1-BCC34,35是一种简单的近似计算RESP电荷的方法,其电荷是在AM1电荷(即AM1半经验方法56获得的波函数产生的Mulliken电荷)基础上进行键电荷校正(BCC)得到的.校正过程只依赖于原子类型和原子间连接关系.校正参数拟合自2755个种类多样的有机分子的HF/6-31G*下的RESP电荷.例如甲醇中的碳原子形成三个“Csp3-single-H”键和一个“Csp3-single-Osp3”键,根据查寻事先拟合的BCC参数就可得知校正电荷应为3×0.0274+1×0.0835= 0.1657(本文电荷单位均为原子单位),加到碳的AM1电荷上就是AM1-BCC电荷.

2.9 MMFF94方法

Merck分子力场94(MMFF94)32,33获得电荷的方式在形式上与AM1-BCC十分相似,同样使用键电荷校正过程,即考虑到每个原子形成的化学键的极性来对初始电荷校正.与AM1-BCC不同之处是MMFF94的初始电荷由原子类型直接确定,且参数来自于拟合HF/6-31G*下计算的分子偶极矩及相互作用能.

2.10 CM2方法

电荷模型(CM)系列方法目前包括CM1、57CM2、37,58CM359-61和CM4,62,63它们都是对低级别方法下的Mulliken或Löwdin电荷39进行简单校正的方法,目的是使原子电荷计算出的偶极矩尽可能精确地重现气相实验值或者高精度量子化学计算值.这一类电荷也被用于不同版本的SM系列溶剂模型中.

CM2校正的公式与AM1-BCC和MMFF94的相比略为复杂,CM2电荷可写为

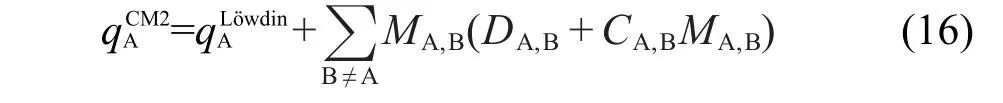
其中M是原子间Mayer键级.64C与D是对实验气相偶极矩拟合的参数,它们取决于化学键的种类,而键的种类仅由它相连的两个原子的元素决定.CM2方法对使用AM1、PM3、HF/MIDI!、HF/6-31G*等级别计算Löwdin电荷的情况分别拟合了校正参数.

2.11 Gasteiger方法

Gasteiger电荷36也被称为轨道电负性部分均衡(PEOE)电荷,这种方法利用了电负性均衡概念,65即电负性不同的原子成键时,电负性较小的原子附近电子密度会流向电负性较大的原子.在这个过程中原先电负性小的原子电负性会增大.当所有原子间电负性相等时,电子密度的分布就是平衡状态分布.

PEOE将原子电负性与原子电荷关系表达为

其中a、b和c为预设参数,对于相同元素但价层轨道处于不同杂化状态的情况参数不同.参数通过实验测定的相应元素的基态和电离态在相应杂化状态下的电离势与电子亲合势来计算.PEOE的迭代过程如同电荷不断在原子间转移的过程,当迭代收敛时电荷分布也就平衡了.在每一步中按照下式计算每一对相连原子间电荷转移量

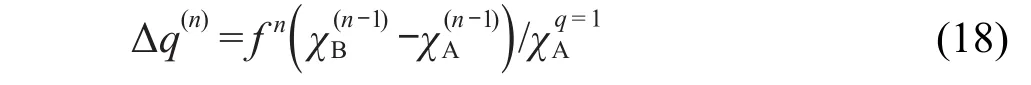
2.12 QEq方法

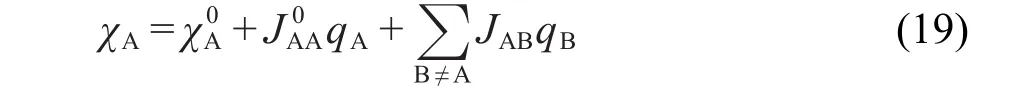
电荷均衡方法(QEq)38得到的是在电负性完全均衡下的原子电荷.电负性表达式为电负性均衡条件要求χ1=χ2=…=χN,它提供了N-1个条件,再将所有原子电荷总和等于分子净电荷作为剩余条件,通过解线性方程即可到得全部原子电荷.式(19)中是广义化的Mulliken电负性为自库仑积分,是原子电离势与电子亲和势的差值.JAB描述了原子间静电作用,若两原子距离较远,则JAB= 1/rAB;若原子间距离较近,电子云静电屏蔽作用不能忽视,此时JAB被定义为两原子间库仑积分.每个原子用单个Slater函数描述电子密度分布,其中指数通过拟合碱金属卤化物实验偶极矩数据确定,对所有原子都相同.普适型力场UFF66使用的正是QEq电荷模型.

值得一提的是QEq方法可以视为另一种使用广泛的方法电负性均衡方法(EEM)67的变体.然而EEM的经验性较大,不同研究者以不同的目标数据拟合了参数,结果有很大差异,因此不纳入本文的比较.

除了上面涉及的方法外,广义原子极化张量(GAPT)电荷68,69也常出现在文献当中.然而GAPT电荷计算过于耗时(和振动分析耗时相近),实际应用意义很有限,因此并不在本文进行介绍和比较.读者可参看文献25对它的测试和讨论.

3 计算细节和测试体系

下文将对前面介绍的12种方法得到的原子电荷与化学经验相符程度、对偶极矩和静电势的重现性以及基组依赖性进行检验,最后讨论计算耗时以及计算方法的选择.测试体系以研究得最为普遍的有机小分子为主,晶体以及包含重元素的体系不在本文讨论范围内.测试分子皆处于稳定构型,过渡态、激发态、受外场作用等状态也不属于本文涉及范围.实际上,Gasteiger、CM2等包含经验参数的方法也不适用于这些特殊问题.本文所测试的方法分为两组,第一组不依赖于任何参数,包括Mulliken、AOIM、Hirshfeld、ADCH、NPA、MK和AIM,第二组依赖于拟合的参数,包括MMFF94、AM1-BCC、CM2、Gasteiger和QEq.

除了理论方法和基组依赖性部分的讨论外,下文的中性分子、阳离子的结构优化和波函数计算均在HF/6-31G*70-72级别下进行,阴离子的结构优化和波函数计算在HF/6-31+G*73级别下进行.波函数的计算和结构优化,以及Mulliken、NPA、MK、CM2、QEq电荷的计算都通过Gaussian 03程序74完成.计算CM2电荷时的初始电荷由HF/6-31G*级别获得.为了使拟合质量较好,计算MK电荷时通过IOp(6/ 42=6)选项将每单位面积的拟合点由默认的1个增加到6个.Hirshfeld和ADCH电荷通过我们开发的Multiwfn 2.1.2程序75计算.AIM电荷通过AIMALL 10.05.04程序76计算.AOIM电荷由AOIM 1.1程序77计算(目前没有其它公开的程序可以计算AOIM电荷).MMFF94电荷通过Avogadro 1.0.3程序78获得. AM1-BCC和Gasteiger电荷由AmberTools 1.5程序79计算.由于计算AM1-BCC电荷前AmberTools会自动在AM1下进行结构优化,我们通过修改代码将此步骤取消.

4 普通小分子的原子电荷

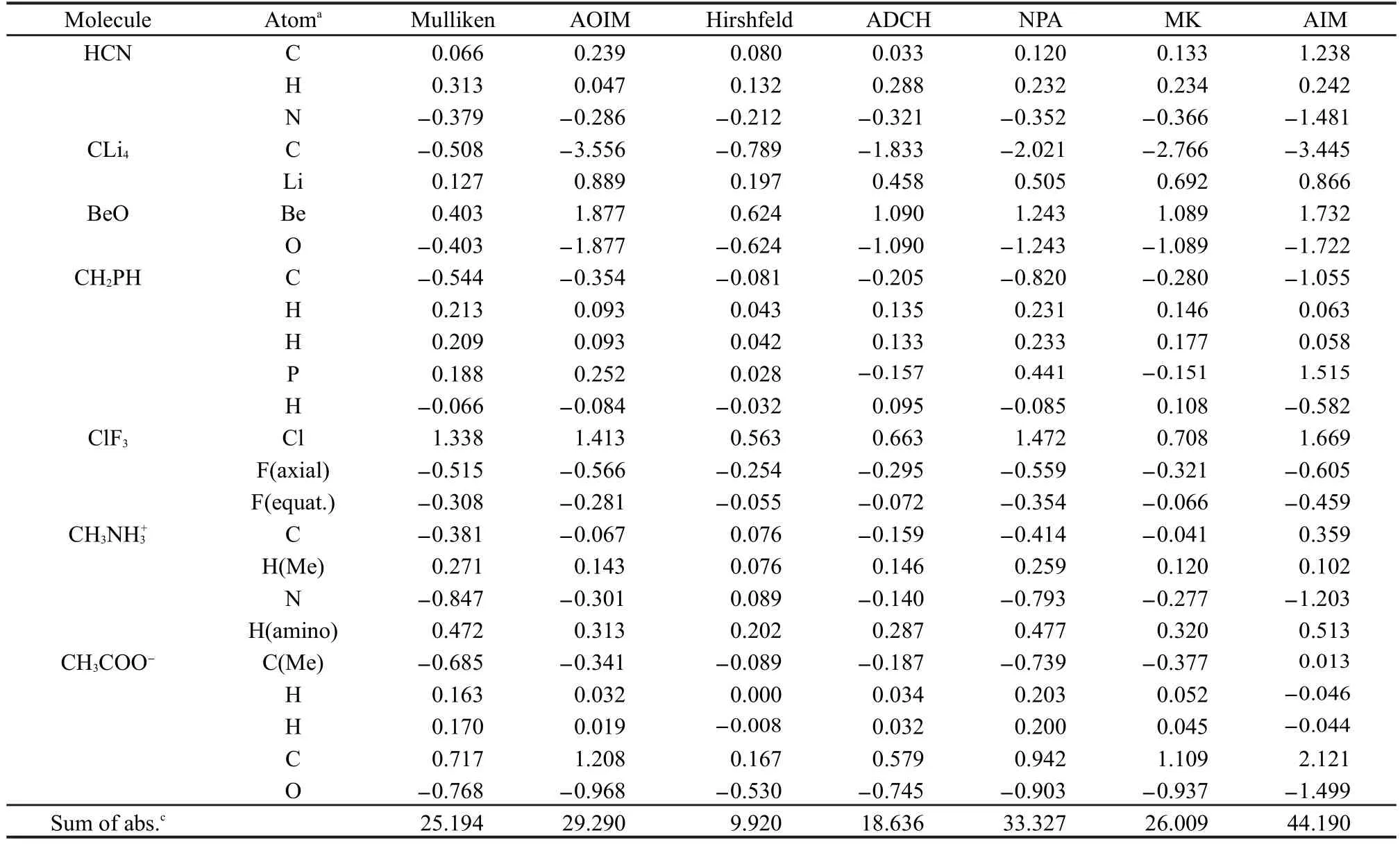
我们首先检验不同方法计算的种类各异的小分子电荷,表1列出了第一组方法计算的结果.容易看出,不同方法得到的原子电荷的数值大小在整体上有所不同.Hirshfeld电荷整体偏小,许多原子电荷的大小都不足0.1.ADCH是对Hirshfeld方法的校正,校正后原子电荷普遍增大,电荷绝对值加和比校正前增加了一倍.对于碳、氢、氮、氧构成的中性有机分子,Mulliken、AOIM、MK和NPA电荷在数量级上比较接近,对于个别分子它们也存在着明显差异,例如ClF3中氯的MK电荷仅为Mulliken、AOIM和NPA方法计算的约一半.很多原子的AIM电荷明显大于其它方法所得电荷,例如丙酮的氧的电荷达到-1.35,氰化氢的氮的电荷高达-1.48.从电荷绝对值加和来看,AIM计算的电荷值(44.19)达到了Hirshfeld计算的电荷值(9.92)的将近5倍.

表1 第一组方法计算的一些小分子的原子电荷Table 1 Atomic charges of some small molecules calculated by the first group of methods

continued Table 1

Mulliken电荷对于CLi4和BeO这样高离子性的体系明显偏小,甚至小于Hirshfeld方法.这和交叉项的平分处理有直接关系,它导致了本应属于阴离子的电子被过多地划归到了阳离子上.而对这样的体系AOIM电荷则比较大,这是由于在分子环境中优化STO的指数后,阴离子的STO较为弥散,一定程度侵入到阳离子空间内,而阳离子的STO较为紧缩,因此在新的基函数下做Mulliken分析时阴离子能够获得更多的电子.

电荷的大小与其合理性并没有绝对关系,考察原子电荷的合理性关键之一是看它能否与一般化学经验、化学观念相吻合.磺酸基是间位定位基,因此苯磺酸的间位碳的原子电荷应当比邻对位更负,第一组方法中除了AIM以外都正确地给出了预期的结果,而AIM方法却认为间位碳的电荷大于对位的.可见AIM电荷对于研究反应位点并不适合.对于偏二甲肼,由于碳的电负性大于氢,因此氨基氮的电荷应当比中间的氮原子的电荷更负,而只有AIM方法给出的结论是相反的.磷的Pauling电负性比碳略小,因此在CH2PH中磷的Mulliken、AOIM、NPA、Hirshfeld电荷为不很大的正值并不意外.而ADCH和MK电荷更侧重于等效描述电子密度的实际分布,由于磷的孤对电子产生的极化效应,使得磷的ADCH和MK电荷都为不大的负值,这也是合理的.而AIM给出的磷的电荷高达1.51,明显缺乏合理性.

在HF/6-31G*波函数级别下计算乙炔的AIM电荷时出现了前文谈到的“赝原子”,它位于两个碳原子之间.由于乙炔的对称性,我们将赝原子盆内电荷积分值平分给两个碳原子来获得碳的AIM电荷,但是当体系缺乏这样的对称性时就不能这样计算AIM电荷了.很多含有炔基的分子也都存在这样的赝原子,这使得AIM方法的适用性受到一定限制.值得一提的是,将基组替换为与6-31G*级别较为相似的SVP基组80后赝原子随即消失,并变为碳-碳间的键临界点,这显示出在特殊情况下AIM的适用性明显受基组影响.

表2列出了第二组方法计算的小分子的原子电荷,由于缺少参数,其中删去了表1中的BeO和CLi4.很明显Gasteiger电荷相对其它电荷明显整体偏小,而MMFF94和AM1-BCC电荷通常比CM2和QEq电荷稍大.从所列分子上看,AM1-BCC和CM2电荷都与经验观念基本一致.由于MMFF94电荷计算方法过于简单,没有考虑电子效应的影响,所得苯磺酸的邻、间、对碳原子电荷相同,均为-0.15,是不合理的.Gasteiger和QEq方法计算的苯磺酸的硫原子电荷都不合理,数值接近0.由于硫原子与三个电负性明显比它更大的氧原子相连,故硫原子电荷理应为较大的正值,其它电荷计算方法的结果也验证了这一点.另外Gasteiger电荷并没有正确预测出苯磺酸的间位碳具有比对位的碳更负的电荷,对这种体系有必要改用明确考虑共轭效应的Gasteiger电荷改进方法,即PEPE方法.81,82

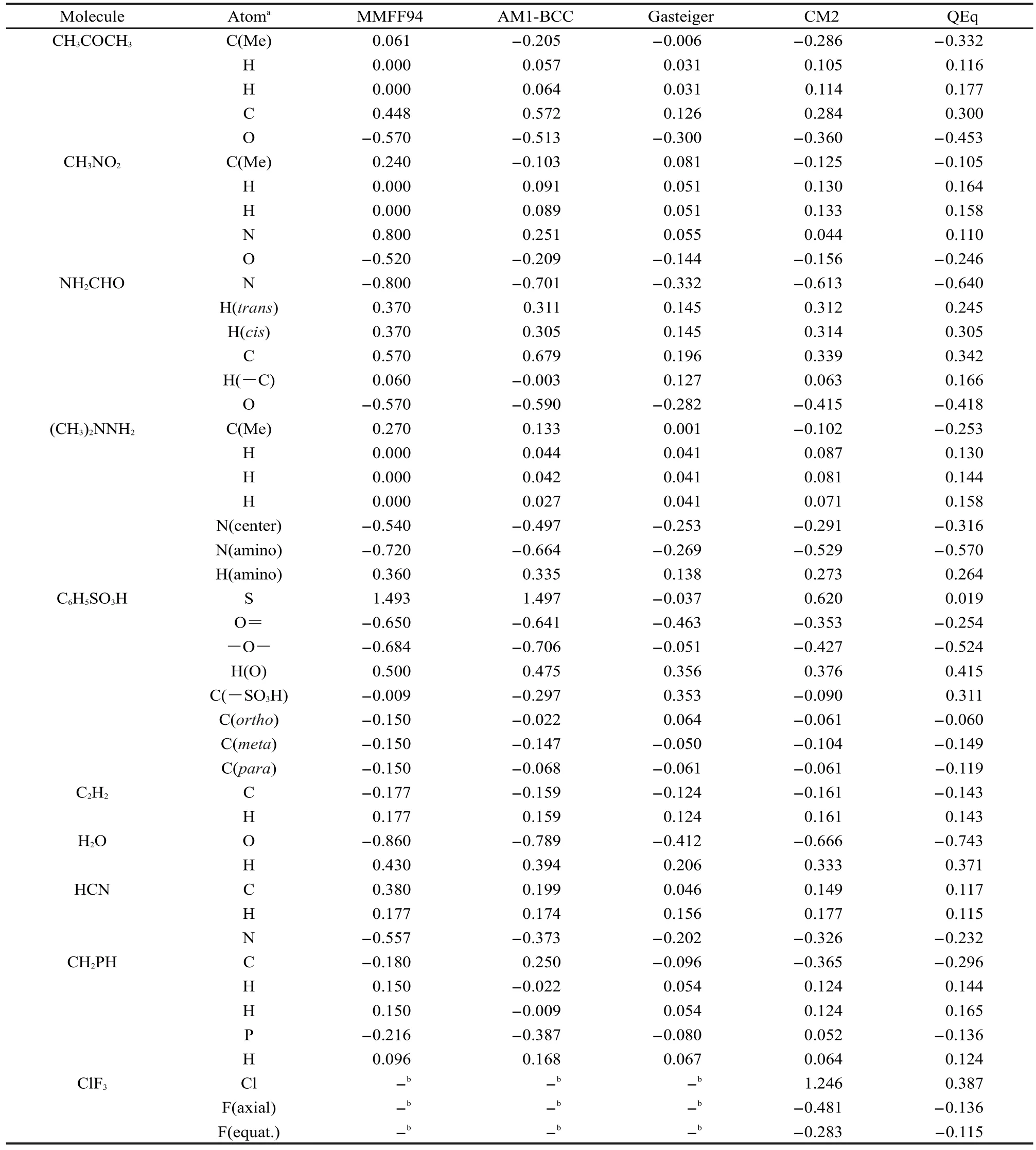
表2 第二组方法计算的一些小分子的原子电荷Table 2 Atomic charges of some small molecules calculated by the second group of methods

continued Table 2

图1 第一组方法计算的甲烷的甲基电荷与取代原子电负性的关系Fig.1 Relationship between methyl charges calculated by the first group of methods and electronegativity of substituent atoms of methane

5 原子电荷与电负性的相关性

对于由σ键构成的典型分子,合理的原子电荷计算方法应当能够与电负性规则基本吻合.对甲烷以不同电负性原子进行取代,各种方法计算的甲基的电荷(甲基各原子电荷的加和)如图1和图2所示. Mulliken、AOIM、NPA、Hirshfeld、ADCH、Gasteiger、CM2和QEq虽然在曲线整体斜率以及曲线形状上有别,但是都正确显示出甲基电荷随着取代基原子电负性增大而逐渐增加.MMFF94和AIM方法计算的甲烷中甲基电荷基本为0,然而从碳、氢的电负性上来看此时甲基电荷理应为负值.MK方法对于氮、氧、氟取代甲烷体系给出的结果与电负性关系不相符,随着取代原子电负性的增加甲基的MK电荷不增反降.出现这种情况主要原因在于在这三种甲烷取代物中氮、氧、氟的电子极化程度依次减小,如果用原子偶极矩,即式(10)来表示极化程度,则数值分别为0.296、0.237和0.143 a.u..原子核附近电子极化对分子外侧静电势产生的影响会等价地体现在拟合静电势方法获得的电荷中,并且由于在这三种体系中电子极化效应对MK电荷的影响超过了电负性差异的影响,因此MK电荷表现出与电负性规则相反的变化趋势.由于AM1-BCC是对拟合静电势电荷的近似,故它对于氮、氧取代甲烷体系给出的结果与电负性关系相违背也是预料之中的.由于ADCH对Hirshfeld电荷的校正过程中使电子密度极化效应得以等效体现,与拟合静电势方法有一定共通之处,这导致对于氮、氧、氟取代时ADCH的甲基电荷的变化曲线的斜率略小于Hirshfeld的斜率.然而ADCH并没有像MK电荷那样违背电负性规律,因此在这一点上比MK具有更强的合理性.

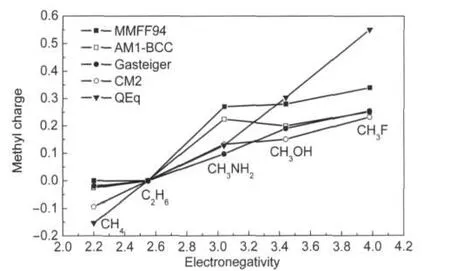
图2 第二组方法计算的甲烷的甲基电荷与取代原子电负性的关系Fig.2 Relationship between methyl charges calculated by the second group of methods and electronegativity of substituent atoms of methane

对甲烷以不同数目的氟进行取代时每个氟原子的电荷应有所不同.1至4取代时每个氟原子所连基团分别相当于―CH3、―CH2F、―CHF2和―CF3,基团电负性依次增加,因此合理的方法计算出的氟原子电荷应当依次减小.由图3、图4可见,Mulliken、Hirshfeld、ADCH、CM2、Gasteiger、QEq方法计算的结果都完全符合这个趋势,而且氟原子电荷的减小是接近线性的.而其它几种方法则表现出不同程度的不合理性.AOIM电荷与期望的趋势不符,1取代时氟原子的电荷值比2、3、4取代时的都要小,这说明AOIM在理论上,或者计算程序的数值算法上有待修正.从1取代变为2取代时,MK电荷仅减小了0.09,而NPA电荷则基本没有变化.AIM电荷在1至4取代过程中几乎都没有发生变化,甚至1取代变为2取代过程中电荷甚至还增大了0.002(可能由于数值积分误差导致).MMFF94的氟原子电荷始终为-0.340,这是因为MMFF94原子电荷只能考虑相邻原子对它的影响,很明显,这种过于简单的计算电荷的方式并不能准确描述原子在分子中的状态. AM1-BCC也未能很好表现氟原子电荷应有的变化趋势,虽然随取代数目增加氟原子电荷确实依次减小,但是曲线却过于平坦.

图3 第一组方法计算的不同取代数目的氟代甲烷的氟原子电荷Fig.3 Atomic charge of fluorine atom calculated by the first group of methods of fluomethane with different numbers of substitutionsTheAIM charge of fluorine atom is too large to be shown on the graph,the values are-0.742,-0.744,-0.744,and-0.737 respectively for 1 to 4 substitutions.

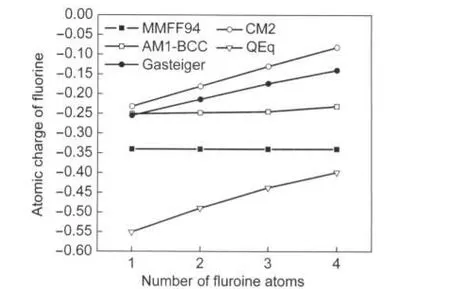
图4 第二组方法计算的不同取代数目的氟代甲烷的氟原子电荷Fig.4 Atomic charge of fluorine atom calculated by the second group of methods for fluomethane with different numbers of substitutions

6 偶极矩的重现性

偶极矩是小分子电荷分布的最简单也是最重要的描述,分子偶极矩重现性的好坏是判断原子电荷合理性重要的客观标准.我们选取了20种具有结构特征不同、有代表性,并且已知实验偶极矩的小分子,对各种方法所得电荷的偶极矩重现性进行了测试,结果列于表3和表4.注意对于第一类电荷计算方法,只有将原子电荷计算的偶极矩与计算电荷时所用的波函数的偶极矩期望值相互比较才是有意义的,直接与实验值相比较是没有意义的,表4显示当前所用的HF/6-31G*波函数偶极矩期望值普遍大于实验值(平均大0.26 Debye(1 Debye=3.338× 10-30C·m)),这主要是由于忽略了相关作用导致的. ADCH是偶极矩保守的方法,因此ADCH电荷计算的偶极矩与偶极矩期望值完全相符.由于静电势、偶极矩都是分子实际电荷分布的客观反映,因此以重现静电势为目的的MK电荷也显示出很好的偶极矩重现性.有人提出在拟合静电势的过程中将偶极矩能够精确重现作为限制条件,85但实际上这么做已没有必要.Mulliken方法的偶极矩重现性从统计结果上看并不理想,对个别分子其偶极矩误差很大,例如噻吩偶极矩期望值为0.90 Debye,而Mulliken方法却认为这是一个几乎无极性的分子.需要指出的是Mulliken电荷的基组依赖性很大,因此Mulliken电荷的偶极矩重现性也可能会随基组的不同而有一定变化.AOIM的偶极矩重现性比Mulliken稍有提高.Hirshfeld方法计算的偶极矩从平均无符号误差(MUE)上看比Mulliken方法更差,而平均含符号误差(MSE)显示Hirshfeld的偶极矩是显著偏低的,这与Hirshfeld电荷偏小有直接关系.NPA电荷的偶极矩重现性很不理想,有高估偶极矩的倾向,尤其是对PF3的偶极矩高估了4.2倍,而对二甲硫醚的偶极矩却低估了10倍以上.AIM电荷对分子偶极矩基本没有重现能力,MUE高达3.00 Debye,这个值已经大于大多数小分子偶极矩.AIM的偶极矩误差主要来自于高估,这很大程度上是由于AIM电荷数值过大所导致的.

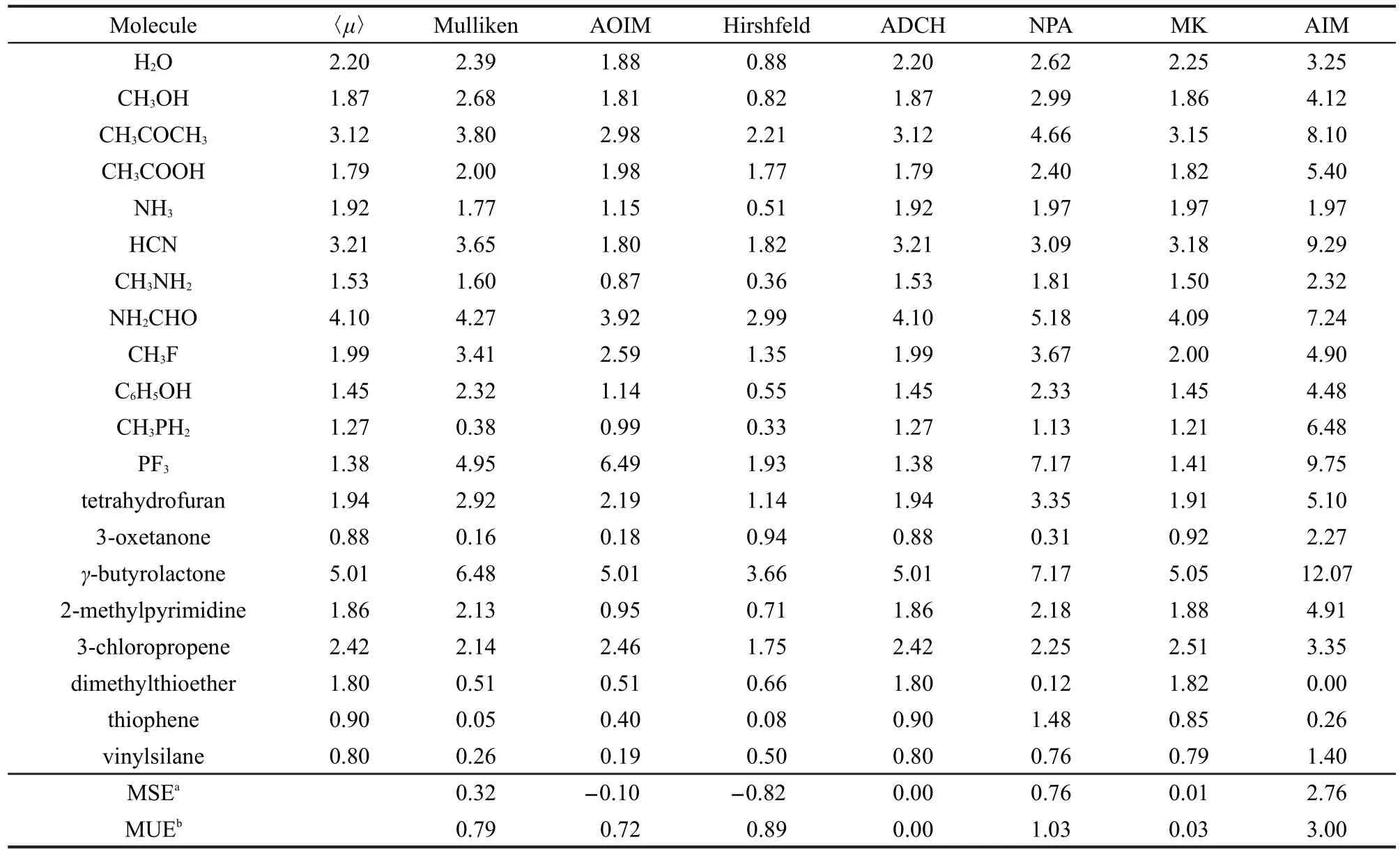
表3 第一组方法计算的20种小分子的分子偶极矩(单位为Debye)以及与HF/6-31G＊级别下偶极矩算符期望值(〈μ〉)的比较Table 3 Molecular dipole moment(unit in Debye)of twenty small molecules calculated by the first group of methods,compared to the expected value of dipole moment(〈μ〉)operator at the HF/6-31G＊level

在拟合参数过程中,MMFF94的参数主要来自于使MMFF94电荷产生的偶极矩逼近HF/6-31G*密度产生的分子偶极矩,AM1-BCC的参数来自于使AM1电荷在校正后逼近HF/6-31G*级别下计算的RESP电荷.它们都使用HF/6-31G*下的数据作为目标数据是因为这个波函数级别对偶极矩的高估被认为可以等效反映出分子在凝聚相中存在的极化效应,因此MMFF94和AM1-BCC的偶极矩应当与HF/6-31G*下的偶极矩期望值相比较.从表4可见这两种电荷的偶极矩重现性对大部分分子基本可以令人满意,MMFF94的MUE为0.36 Debye,虽然AM1-BCC和MMFF94在键电荷校正过程中很相似,但AM1-BCC的MUE更小,为0.25 Debye,其改善在一定程度上可能是由于AM1-BCC使用了更有意义的初始电荷.Gasteiger的偶极矩重现性无论以气相实验值为参考还是以HF/6-31G*偶极矩为参考都显得一般,并且对多数分子有低估偶极矩的倾向.CM2电荷能够很好地重现气相实验偶极矩, MUE仅为0.15 Debye,对所有分子都没有出现过大误差,这与CM2提出的目标完全相一致.QEq对实验偶极矩和HF/6-31G*下的偶极矩重现性都很不理想,对许多分子偶极矩高估了近一倍甚至一倍以上,严重低估偶极矩的情况同样存在,如2-甲基嘧啶.

表4 第二组方法计算的20种小分子的分子偶极矩(单位为Debye)以及与HF/6-31G＊级别下偶极矩算符期望值和气相实验值的比较Table 4 Molecular dipole moment(unit in Debye)of twenty small molecules calculated by the second group of methods, compared to the expected value of dipole moment operator at the HF/6-31G＊level and gas-phase experimental value

综上所述,Mulliken、AOIM、Hirshfeld、NPA、Gasteiger、QEq电荷,尤其是AIM电荷,对偶极矩重现性都不好.ADCH和MK都能很准确重现波函数的偶极矩期望值,若波函数完全精确,则这两种电荷计算的偶极矩将与气相的实际值相一致,而利用CM2方法则可以在较低波函数级别下很准确地预测气相偶极矩.MMFF94和AM1-BCC能够较好地重现HF/6-31G*的偶极矩.

7 静电势的重现性

当研究的问题涉及分子间较近距离的静电相互作用时偶极模型显得过于简单,只有分子范德华表面外侧精确静电势也能被较好重现时,才说明这种原子电荷适合研究分子间近距离静电作用.又由于静电势是可观测量,因此静电势的重现性与偶极矩一样也是检验原子电荷合理性的重要、客观的指标.其重现性常以原子电荷在分子范德华表面外侧所取的格点位置上产生的静电势VModel与波函数计算的精确静电势VReal之间的相对均方根偏差(RRMSE)来反映,计算公式为

我们选取了21种中性分子和4种离子用于测试不同原子电荷计算方法的静电势重现性,见表5和表6.其中既包含一部分测试偶极矩重现性所用的小分子,也包含结构更复杂的生物、药物分子.计算RRMSE所用格点设定与计算MK电荷时的一致,参考静电势在HF/6-31G*级别下获得.

由于MK电荷正是通过最小化静电势重现性误差得到的,因此它的RRMSE拥有理论最低值.从RRMSE的平均值上看,其余11种方法的静电势重现能力可以大致分为四个档次:(1)重现性很好,平均RRMSE在0.25上下.这一类包括ADCH、MMFF94、AM1-BCC和CM2.如果改用能够比较准确地重现气相偶极矩的波函数,即使用B3LYP/ cc-pVTZ波函数代替HF/6-31G*去计算参考静电势,则CM2的平均RRMSE值会从0.268降低到0.228.(2)重现性不错.AOIM属于此类,平均RRMSE为0.337.(3)重现性一般,RRMSE平均值在0.4-0.6.包括Mulliken、Hirshfeld、NPA、Gasteiger和QEq.(4)重现性很差,这一类只包括AIM,平均RRMSE高达1.53.

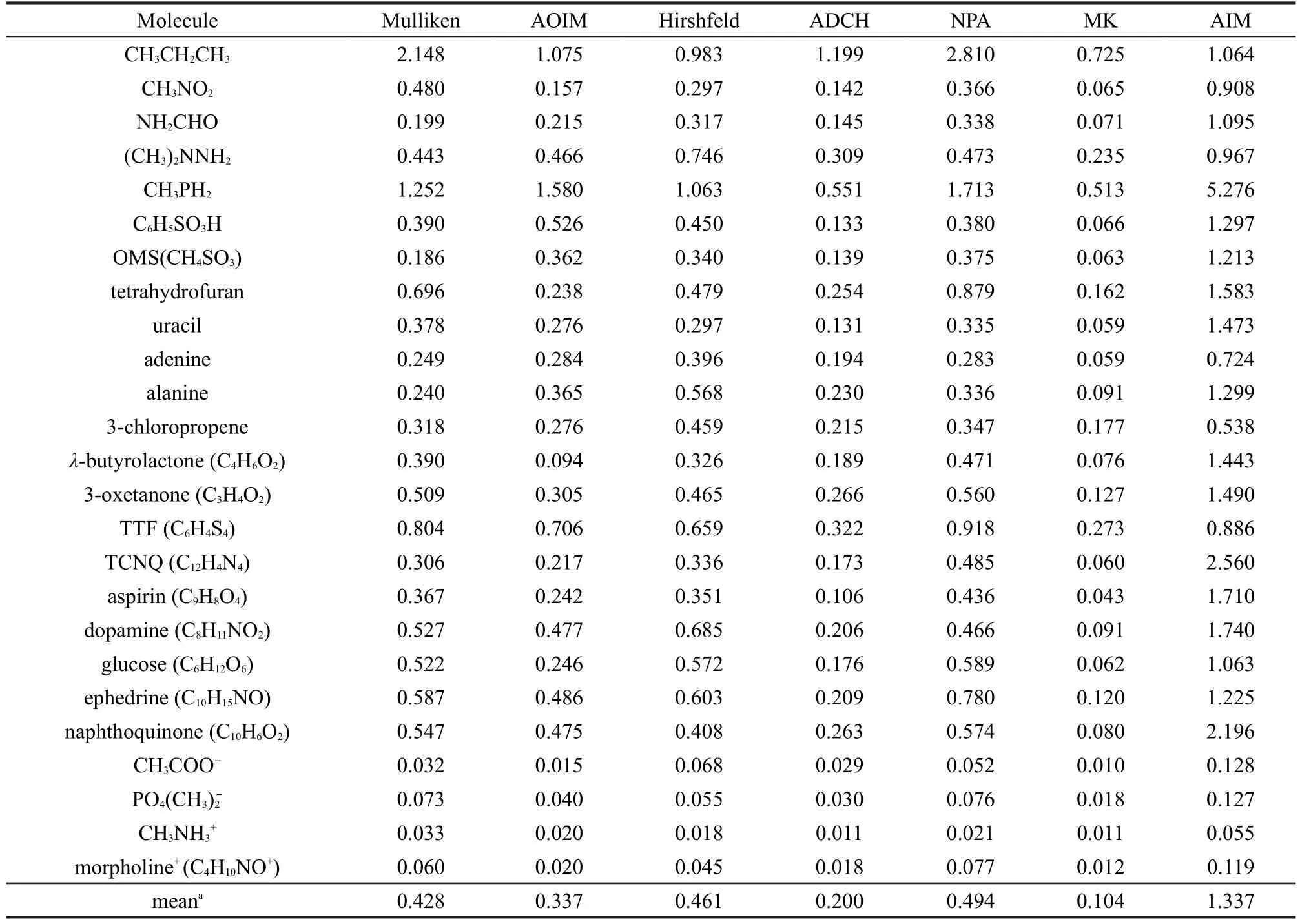
表5 第一组方法产生的静电势相对于HF/6-31G＊级别下精确静电势的相对均方根偏差Table 5 Relative root mean square error(RRMSE)of the ESPproduced by the first group of methods relative to the exact ESPat the HF/6-31G＊level

通过检验MK电荷的数据,可以看出原子电荷模型本身对于一些体系存在明显局限性.对于丙烷和CH3PH2分子,即便是MK电荷,其RRMSE也分别高达0.72和0.51,因此我们未将这两个分子纳入RRMSE平均值的统计中.若想更准确地描述静电相互作用,即降低RRMSE,就必须增加一些非原子中心的点电荷,或者在原子中心引入点多极矩.25若在计算MK电荷时在每个原子中心都引入一个点偶极矩(点偶极矩向量与原子电荷一起被拟合),则丙烷和CH3PH2分子的RRMSE会分别降至0.22和 0.13,静电势重现性大大提高.而对于一些体系用原子电荷模型表现静电势是足够准确的,如MK电荷对Aspirin的RRMSE仅有0.043.

从表中可见所有方法对离子的静电势重现性都显著好于中性分子,RRMSE降低了约一个数量级.出现这种情况是由于带电分子外围静电势主要由分子单极矩所主导,而所测试的所有原子电荷计算方法都是单极矩保守的,即原子电荷加和等于分子净电荷.不同方法对带电分子静电势重现性的优劣关系和中性分子情况是相似的.

8 波函数质量的依赖性

图5比较了第一类方法计算的乙酸的甲基碳原子电荷的基组依赖性,从左到右基组完备性逐渐增加.从STO-3G86提升至3-21G87的过程中各种方法计算的结果都有不同程度的变化,通常被认为具有很好基组稳定性的NPA电荷的变化值甚至大于公认基组稳定性差的Mulliken电荷.注意由于极小基的完备性很低,所以提升至分裂价基后结果的明显变化并不能说明方法的合理性差.从6-311G**88开始除了Mulliken方法外所有方法的结果都已经收敛,提升至aug-cc-pVTZ89,90的过程中结果变化都不显著.其中Hirshfeld和ADCH电荷收敛得最早,从3-21G开始就基本不发生变化.同时也说明ADCH对Hirshfeld电荷的校正并没有破坏Hirshfeld电荷良好的基组稳定性.MK和AOIM从6-31G*开始收敛,而NPA和AIM收敛得相对稍迟.唯一不能随基组增加而收敛的方法是Mulliken,曲线在基组增大过程中始终强烈波动,对6-311G**基组下重原子增加弥散函数成为6-311+G**73后,其它方法得到的甲基碳电荷变化均不超过0.01,而Mulliken电荷数值则降低了0.15,这是因为碳的弥散函数严重侵入到了氢的原子空间内,原本在6-311G**基组下属于氢的电子密度现在有一部分被碳的基函数所描述,因此氢的电子占据数一部分被归属到了碳.而进一步提升到6-311++G(2df,2p)73后,由于氢的弥散函数也明显侵入到了碳的原子空间内,碳的电子占据数有不少被划归给了氢,因此碳的Mulliken电荷又增加了许多.6-311++G(2df,2p)已经是完备性很高的基组,继续提升质量后原子电荷应当不出现明显改变,然而提升至aug-cc-pVTZ后Mulliken电荷变化却仍高达0.43.因此从基组依赖性的角度上讲, Mulliken方法是存在严重缺陷的,没有办法“唯一”地获得Mulliken电荷,基组的轻微改变就可能使结果有定性的变化.同时也说明提升基组质量并不会提升Mulliken电荷的合理性,用大基组计算Mulliken电荷是没有意义的.实际上大基组,尤其是包含弥散函数的情况,基函数的化学意义往往比较差,与原子轨道缺乏对应性,而极小基则能够与原子轨道相互对应,会使Mulliken方法的计算过程更有物理意义.以上的讨论对于乙酸的其它原子的电荷也同样适用.

表6 第二组方法产生的静电势相对于HF/6-31G＊级别下精确静电势的相对均方根偏差Table 6 RRMSE of the ESPproduced by the second group of methods relative to the exact ESPat the HF/6-31G＊level

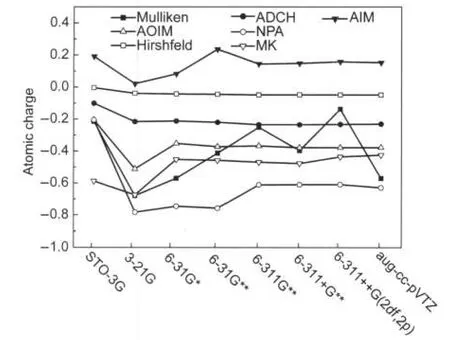
图5 不同方法结合不同基组在Hartree-Fock级别下获得的乙酸的甲基碳原子电荷Fig.5 Atomic charge of methyl carbon of acetic acid calculated by different methods under various basis-sets at the Hartree-Fock level

第一类方法对计算波函数所用理论方法的依赖性如图6所示,其中包括不含相关效应的Hartree-Fock方法、广义梯度近似(GGA)泛函BP86、91,92杂化泛函B3LYP,93以及MP2和CCSD70方法,基组均使用cc-pVDZ.89由于相关效应对多重键影响较大,所以这里选取乙酸的羰基氧原子用于测试.由于AOIM 1.1程序只能读取SCF波函数,因此MP2和CCSD的结果未在图中显示,但实际上利用自然轨道形式不难将AOIM的应用范围扩展到后HF波函数上.从图6可见对于任何一种计算原子电荷的方法,无论通过何种方式引入相关效应,所得结果都很相近,数值差异最大不超过0.05.而Hartree-Fock波函数和各种相关波函数下的计算结果却差异明显,引入相关效应后所有方法给出的羰基氧原子电荷均明显减小,这反映出相关效应会减小化学键的极性这一普遍现象.通过检验乙酸各个原子的电荷会发现Hirshfeld和ADCH电荷受电子相关效应影响相对于其它方法更弱,比如BP86下Hirshfeld和ADCH的羰基氧原子电荷相对于Hartree-Fock下的结果差异分别为0.07、0.09,而Mulliken、AOIM、NPA、MK和AIM电荷变化分别为0.16、0.13、0.13、0.12和0.18.

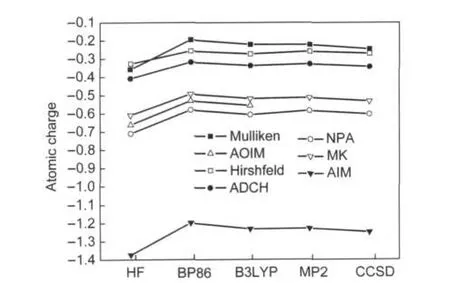
图6 不同方法结合cc-pVDZ基组和不同哈密顿得到的乙酸的羰基氧原子电荷Fig.6 Atomic charge of carbonyl oxygen of acetic acid calculated by different methods in combination with cc-pVDZ basis-set and various Hamiltonians

由上可见,至少对于普通有机分子,获得原子电荷并不需要高级别后HF方法计算波函数,选择适当的密度泛函方法计算的波函数就可以满足要求.对于NPA、MK、AIM,尤其是Hirshfeld和ADCH方法,只需要中等质量的基组就已经足够.在此之上继续提高波函数质量意义不大.

9 计算的耗时

计算方法的耗时大小直接关系到它的适用领域.计算耗时不仅取决于方法本身的复杂度,也明显依赖于计算程序的代码效率、数值方法和编译、运行时的软硬件环境.另外,很多方法的可变参数也会影响耗时,比如AIM、Hirshfeld方法中对积分的期望精度、AOIM的L-BFGS-B步骤中的收敛阈值、静电势拟合时拟合点的密度等.本节对各种方法计算耗时的讨论只是定性的,计算耗时以当前普通实验室的计算能力作为参照.

MMFF94、Gasteiger和QEq方法由于不依赖于波函数,方法本身也比较简单,所以计算这三种电荷总耗时极小,即使对于几千个原子的体系也可以在数秒内给出结果,它们也能够用于需要高效计算大批量小分子电荷的情况,比如药物高通量筛选.由于QEq计算量小,而且是依赖于几何结构的,能反映出原子电荷对周围环境变化的响应,因此QEq可以作为浮动电荷力场94的电荷模型,即在动力学/蒙特卡罗模拟过程中每隔一定步数或构象改变一定程度后自动更新原子电荷.

AM1-BCC电荷的计算总耗时完全来自于AM1单点计算,BCC校正过程几乎不需要耗时.对于几十个原子体系的AM1计算,通常在数秒内能够完成.对于数百个原子的体系,AM1计算就较为耗时,而上千个原子的体系则十分困难.但是如果使用线性标度方法,如MOZYME方法95来加速AM1步骤,则AM1-BCC电荷的适用范围可以被大大扩展.

得到波函数后,计算Mulliken电荷不需要额外耗时,而计算NPA、MK、Hirshfeld和ADCH电荷的计算耗时也只占波函数计算耗时的很小比例.因此可以近似认为计算这几种电荷的总耗时就是计算波函数的耗时.

使用AOIM 1.1程序计算基组较大或原子数稍多体系的AOIM电荷比较慢.例如在HF/6-31G*下计算Ephedrine(C10H15NO)分子的AOIM电荷耗费约8 min,而使用默认参数、单线程下使用Gaussian 03计算这个分子波函数耗时40 s.我们认为计算速度缓慢不是AOIM理论本身的原因,而是因为AOIM 1.1代码中的L-BFGS-B最小化模块效率有待改善.对代码和算法进行优化和并行化后有望使AOIM电荷计算速度显著加快.

AIM电荷计算耗时极长.我们使用计算效率较高的AIM程序AIMALL,并采用默认的积分精度和积分算法时,计算Ephedrine分子全部AIM电荷总耗时为10.5 min,是计算波函数时间的近16倍.AIM电荷计算费时是因为AIM的原子边界复杂,导致原子盆不容易被准确积分,尽管已有不少研究者探索出更有效的原子盆积分方法,96-98但AIM电荷计算缓慢的问题始终没有被彻底解决.

CM2的校正步骤几乎不需要额外时间,总耗时取决于使用何种理论级别计算初始电荷.如果要求计算快速,可以用半经验方法,如果要求对实际气相偶极矩有更好的重现能力,则可以用从头算方法.实际上从原文献的统计数据来看,半经验与从头算方法所得CM2电荷的偶极矩重现能力对于多数体系差距并不很大.

10 计算方法的选择

结合上文对各种原子电荷计算方法的对比结果、方法特点以及目前应用的现状,我们对原子电荷计算方法的选择给出以下建议.

对于分子体系的量子化学研究,建议使用NPA和ADCH电荷.NPA电荷目前应用十分广泛,合理性总体表现较好.但注意不宜使用NPA电荷分析静电相互作用,同时注意NPA用于过渡金属、镧系锕系金属时存在一定问题.23,99问题主要是由于这些元素的极小集/里德堡集划分标准比较含糊,而不同的划分又会影响OWSO过程,进而影响电荷数值.最近提出的ADCH方法无论在电荷合理性、基组依赖性、偶极矩重现性和静电势的重现性上都表现不错,电荷计算时间也远小于波函数计算时间,是十分有前景的原子电荷计算方法,其普适性、稳定性有待在更多的实际应用中进行检验.

基于原子电荷的分子模拟任务需要原子电荷能够较好地描述静电相互作用.通常来说以MK为代表的拟合静电势电荷是最适合用于分子模拟的.但如果模拟的是有机分子,更适宜使用RESP电荷,因为它解决了普通拟合静电势方法存在的构象依赖性、内部原子电荷数值不稳定性和原子等价性问题,若这些问题存留则可能会影响模拟过程的合理性.注意由于在拟合力场参数时范德华作用、1-4位相互作用和静电作用是相互耦合的,故范德华参数和二面角参数对电荷模型有依赖性,因此若模拟任务依赖于已有力场参数,则原子电荷的计算方法应当尽量与力场原文中的方法一致.

对于较大分子体系或者大量有机小分子体系的原子电荷的计算建议使用AM1-BCC方法,此方法表现静电作用较好且计算速度较快.如果需要进一步降低计算耗时,可以改用MMFF94方法.另外,如果所研究的大分子体系结构具有规律性,如蛋白质、多糖、核酸、高分子,也可以使用能够更好重现静电势的MK方法获得每个片段的电荷再进行拼接.

估算气相分子偶极矩最适合使用CM2方法,可以以较低的计算花费获得很精确的气相偶极矩.

最后,本文对目前使用广泛的Mulliken、AIM和Gasteiger电荷进行简要评述.

Mulliken方法尽管存在原理不严格、低估离子性化合物的键的极性、基组依赖性大、偶极矩和静电势重现性差等诸多缺陷,但是从本文的测试看到,Mulliken电荷对于多数小分子并没有出现过于明显的不合理性,又由于Mulliken电荷几乎被所有量子化学软件支持,不耗费额外计算时间,因此Mulliken电荷虽然不推荐使用,但仍可以作为定性的参考.在极小基下产生的Mulliken电荷比在更高级别基组下产生结果在原理上更合理.如果所用基组包含弥散函数,则应当舍弃Mulliken电荷.另外,由于Mulliken电荷受基组影响明显,比较Mulliken电荷时应注意必须处于在相同基组下,否则结果没有意义.

AIM方法一般不建议使用.尽管它拥有严格的物理解释,但是在测试中它的结果往往明显违背化学观念,对偶极矩和静电势重现性都很差,当体系存在赝原子时无法使用,而且计算耗时极长.

Gasteiger电荷由于具有计算方便、快速的特点,被很多药物设计、分子对接软件所采用,常被用于描述受体-配体静电相互作用、生成CoMFA任务所需要的静电势场.然而从前文的对比结果可见它的静电势重现性并不理想,因此并不推荐Gasteiger电荷用于这些场合.相比之下使用AM1-BCC和MMFF94电荷更为合适.

11 总 结

原子电荷是十分古老、简单的模型,可以追溯到化合价概念的提出.随着理论化学的发展以及人们对电子结构认识的加深,原子电荷模型不仅没有被遗弃,新的计算方法还在不断涌现,这是由于它有着重要的理论和实用意义.本文介绍了目前使用最为广泛的12种计算原子电荷的方法,通过大量分析对它们的特点进行了全面的比较和评述.对比分析中显示,许多计算方法的结果间存在很大差异,错误地选用计算方法可能得到不可靠甚至没有意义的原子电荷.只有充分掌握了众多计算方法各自的原理和特点,才能根据实际问题选择最为适用的一种.

(1)Qian,B.H.;Ma,W.X.;Lu,L.D.;Yang,X.J.;Wang,X.Acta Phys.-Chim.Sin.2010,26,610.[钱保华,马卫兴,陆路德,杨绪杰,汪 信.物理化学学报,2010,26,610.]

(2) Zheng,W.R.;Xu,J.L.;Xiong,R.Acta Phys.-Chim.Sin.2010, 26,2535.[郑文锐,徐菁利,熊 瑞.物理化学学报,2010,26, 2535.]

(3)Shen,T.;Du,F.P.;Liu,T.;Yao,G.W.;Wu,Z.;Fang,M.M.; Xu,X.J.;Lu,H.Z.Acta Phys.-Chim.Sin.2011,27,1831. [申 涛,杜凤沛,刘 婷,姚广伟,吴 峥,方萌萌,徐筱杰,路慧哲.物理化学学报,2011,27,1831.]

(4) Zhou,J.J.;Chen,H.M.;Xie,G.R.;Ren,T.R.;Xu,Z.H.Prog. Chem.1998,10,55.[周家驹,陈红明,谢桂荣,任天瑞,许志宏.化学进展,1998,10,55.]

(5) Ji,G.D.;Zhao,Y.H.;Yuan,X.J.Northeast Normal Univ. (Natural Science Edition)1998,47. [籍国东,赵元慧,袁 星.东北师范大学学报(自然科学版),1998,47.]

(6) Ding,Y.F.;Zhang,Y.;Zhang,D.H.;Li,Z.P.Acta Phys.-Chim. Sin.2010,26,1651.[丁元法,张 跃,张大海,李仲平.物理化学学报,2010,26,1651.]

(7) Laio,A.;VandeVondele,J.;Rothlisberger,U.J.Phys.Chem.B 2002,106,7300.

(8) Pipek,J.;Mezey,P.G.J.Chem.Phys.1989,90,4916.

(9) Elstner,M.;Porezag,D.;Jungnickel,G.;Elsner,J.;Haugk,M.; Frauenheim,T.;Suhai,S.;Seifert,G.Phys.Rev.B 1998,58, 7260.

(10) Giesen,D.J.;Cramer,C.J.;Truhlar,D.G.J.Phys.Chem.1995, 99,7137.

(11) Giesen,D.J.;Hawkins,G.D.;Liotard,D.A.;Cramer,C.J.; Truhlar,D.G.Theor.Chem.Acc.1997,98,85.

(12) Li,J.B.;Hawkins,G.D.;Cramer,C.J.;Truhlar,D.G.Chem. Phys.Lett.1998,288,293.

(13) Thompson,J.D.;Cramer,C.J.;Truhlar,D.G.J.Phys.Chem.A 2004,108,6532.

(14) Meister,J.;Schwarz,W.H.E.J.Phys.Chem.1994,98,8245.

(15) Cramer,C.J.Essentials of Computational Chemistry,2nd ed.; John Wiley&Sons:West Sussex,2004;pp 309-324.

(16) Jensen,F.Introduction to Computational Chemistry,2nd ed.; John Wiley&Sons:West Sussex,2007;pp 293-304.

(17)Young,D.C.Computational Chemistry;John Wiley&Sons: New York,2001;pp 99-105.

(18) Cioslowski,J.Electronic WavefunctionAnalysis.In Encyclopedia of Computational Chemistry;Schleyer,P.v.R. Ed.;John Wiley&Sons:West Sussex,1998;Vol.2,pp 892-905.

(19) Mulliken,R.S.J.Chem.Phys.1955,23,1841.

(20) Mulliken,R.S.J.Chem.Phys.1955,23,1833.

(21) Mulliken,R.S.J.Chem.Phys.1955,23,2338.

(22) Bachrach,S.M.PopulationAnalysis and Electron Densities from Quantum Mechanics.In Reviews in Computational Chemistry;Lipkowitz,K.B.,Boyd,D.B.Eds.;VCH Publishers:New York,1994;Vol.5,pp 171-227.

(23) Clark,A.E.;Sonnenberg,J.L.;Hay,P.J.;Martin,R.L. J.Chem.Phys.2004,121,2563.

(24) Martin,F.;Zipse,H.J.Comput.Chem.2005,26,97.

(25) Wiberg,K.B.;Rablen,P.R.J.Comput.Chem.1993,14,1504.

(26)Lu,H.G.;Dai,D.D.;Yang,P.;Li,L.M.Phys.Chem.Chem. Phys.2006,8,340.

(27) Hirshfeld,F.L.Theor.Chem.Acc.1977,44,129.

(28)Lu,T.;Chen,F.W.J.Theor.Comput.Chem.accepted.

(29) Reed,A.E.;Weinstock,R.B.;Weinhold,F.J.Chem.Phys. 1985,83,735.

(30)Besler,B.H.;Merz,K.M.,Jr.;Kollman,P.A.J.Comput.Chem. 1990,11,431.

(31)Bader,R.F.W.;Beddall,P.M.J.Chem.Phys.1972,56,3320.

(32)Halgren,T.A.J.Comput.Chem.1996,17,520.

(33) Halgren,T.A.J.Comput.Chem.1996,17,616.

(34) Jakalian,A.;Bush,B.L.;Jack,D.B.;Bayly,C.I.J.Comput. Chem.2000,21,132.

(35) Jakalian,A.;Jack,D.B.;Bayly,C.I.J.Comput.Chem.2002, 23,1623.

(36) Gasteiger,J.;Marsili,M.Tetrahedron 1980,36,3219.

(37) Li,J.B.;Zhu,T.H.;Cramer,C.J.;Truhlar,D.G.J.Phys. Chem.A 1998,102,1820.

(38)Rappe,A.K.;Goddard,W.A.J.Phys.Chem.1991,95,3358.

(39) Cusachs,L.C.;Politzer,P.Chem.Phys.Lett.1968,1,529.

(40) Stout,E.W.;Politzer,P.Theor.Chem.Acc.1968,12,379.

(41) Doggett,G.J.Chem.Soc.A 1969,229.

(42) Christoffersena,R.E.;Baker,K.A.Chem.Phys.Lett.1971,8,4.

(43) Bickelhaupt,F.M.;van Eikema Hommes,N.J.R.;Fonseca Guerra,C.;Baerends,E.J.Organometallics 1996,15,2923.

(44) Weinhold,F.Natural Bond Orbital Methods.In Encyclopedia of Computational Chemistry;Schleyer,P.v.R.Ed.;John Wiley& Sons:West Sussex,1998;Vol.2,pp 1792-1811.

(45) Glendening,E.D.;Badenhoop,J.K.;Reed,A.E.;Carpenter,J. E.;Bohmann,J.A.;Morales,C.M.;Weinhold,F.NBO,Version 5.0,2001.http://www.chem.wisc.edu/～nbo5/.

(46) Liu,W.;Li,L.Theor.Chem.Acc.1997,95,81.

(47) Sanchez-Portal,D.;Artacho,E.;Soler,J.M.Solid State Commun.1995,95,685.

(48) Sanchez-Portal,D.;Artacho,E.;Soler,J.M.J.Phys.:Condens. Matter 1996,8,3859.

(49) Bader,F.W.Atoms in Molecules:A Quantum Theory;Oxford University Press:New York,1994.

(50) Nalewajski,R.F.;Parr,R.G.Proc.Natl.Acad.Sci.U.S.A. 2000,97,8879.

(51) Davidson,E.R.;Chakravorty,S.Theor.Chem.Acc.1992,83, 319.

(52) Chirlian,L.E.;Francl,M.M.J.Comput.Chem.1987,8,894.

(53)Breneman,C.M.;Wiberg,K.B.J.Comput.Chem.1990,11, 361.

(54) Sigfridsson,E.;Ryde,U.J.Comput.Chem.1998,19,377.

(55) Bayly,C.I.;Cieplak,P.;Cornell,W.;Kollman,P.A.J.Phys. Chem.1993,97,10269.

(56) Dewar,M.J.S.;Zoebisch,E.G.;Healy,E.F.;Stewart,J.J.P. J.Am.Chem.Soc.1985,107,3902.

(57) Storer,J.W.;Giesen,D.J.;Cramer,C.J.;Truhlar,D.G. J.Comput.-Aided Mol.Des.1995,9,87.

(58) Li,J.B.;Williams,B.;Cramer,C.J.;Truhlar,D.G.J.Chem. Phys.1999,110,724.

(59) Thompson,J.D.;Cramer,C.J.;Truhlar,D.G.J.Comput. Chem.2003,24,1291.

(60) Winget,P.;Thompson,J.D.;Xidos,J.D.;Cramer,C.J.; Truhlar,D.G.J.Phys.Chem.A 2002,106,10707.

(61) Kalinowski,J.A.;Lesyng,B.;Thompson,J.D.;Cramer,C.J.; Truhlar,D.G.J.Phys.Chem.A 2004,108,2545.

(62) Olson,R.M.;Marenich,A.V.;Cramer,C.J.;Truhlar,D.G. J.Chem.Theory Comput.2007,3,2046.

(63) Kelly,C.P.;Cramer,C.J.;Truhlar,D.G.J.Chem.Theory Comput.2005,1,1133.

(64) Mayer,I.Chem.Phys.Lett.1983,97,270.

(65) Sanderson,R.T.Science 1951,114,670.

(66) Rappe,A.K.;Casewit,C.J.;Colwell,K.S.;Goddard,W.A.; Skiff,W.M.J.Am.Chem.Soc.1992,114,10024.

(67)Mortier,W.J.;Ghosh,S.K.;Shankar,S.J.Am.Chem.Soc. 1986,108,4315.

(68) Cioslowski,J.Phys.Rev.Lett.1989,62,1469.

(69) Cioslowski,J.J.Am.Chem.Soc.1989,111,8333.

(70) Szabo,A.;Ostlund,N.S.Modern Quantum Chemistry,1st rev ed.;Dover Publications:New York,1989.

(71) Hariharan,P.C.;Pople,J.A.Theor.Chem.Acc.1973,28,213.

(72) Hehre,W.J.;Ditchfield,R.;Pople,J.A.J.Chem.Phys.1972, 56,2257.

(73) Frisch,M.J.;Pople,J.A.;Binkley,J.S.J.Chem.Phys.1984, 80,3265.

(74) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03, Revison E.01;Gaussian Inc.:Wallingford,CT,2004.

(75) Lu,T.Multiwfn,Version 2.1.2;2011.http://Multiwfn.codeplex. com.

(76) Keith,T.A.AIMALL,Version 10.05.04,2010.

(77) Lu,H.G.AOIM,Version 1.1,2006;http://faculty.sxu.cn/luhg/ aoim.html.

(78)Avogadro:an Open-Source Molecular Builder and Visualization Tool,Version 1.0.3,2011.

(79) Case,D.A.;Darden,T.A.;Cheatham,T.E.C.,III;et al. AmberTools,Version 1.5;2011.

(80) Schäfer,A.;Horn,H.;Ahlrichs,R.J.Chem.Phys.1992,97, 2571.

(81) PETRA Manual.http://www2.ccc.uni-erlangen.de/software/ petra/manual(accessed Sep 12,2011).

(82) Marsili,M.;Gasteiger,J.Croat.Chem.Acta 1980,53,601.

(83) The Open Babel Package,Version 2.3.0;2010;http://openbabel. sourceforge.net.

(84) Sanner,M.F.J.Mol.Graph.Model.1999,17,57.

(85)Woods,R.J.;Khalil,M.;Pell,W.;Moffat,S.H.;Smith,V.H. J.Comput.Chem.1990,11,297.

(86) Hehre,W.J.;Stewart,R.F.;Pople,J.A.J.Chem.Phys.1969, 51,2657.

(87) Binkley,J.S.;Pople,J.A.;Hehre,W.J.J.Am.Chem.Soc.1980, 102,939.

(88) Krishnan,R.;Binkley,J.S.;Seeger,R.;Pople,J.A.J.Chern. Phys.1980,72,650.

(89) Dunning,J.T.H.J.Chem.Phys.1989,90,1007.

(90) Kendall,R.A.;Dunning,T.H.;Harrison,R.J.J.Chem.Phys. 1992,96,6796.

(91) Becke,A.D.Phys.Rev.A 1988,38,3098.

(92) Perdew,J.P.Phys.Rev.B 1986,33,8822.

(93) Becke,A.D.J.Chem.Phys.1993,98,1372.

(94) Patel,S.;Brooks,C.L.Mol.Simul.2006,32,231.

(95) Stewart,J.J.P.Int.J.Quantum Chem.1996,58,133.

(96) Biegler-König,F.W.J.Comput.Chem.2000,21,1040.

(97) Biegler-König,F.W.;Bader,R.F.W.;Tang,T.H.J.Comput. Chem.1982,3,317.

(98)Sanville,E.;Kenny,S.D.;Smith,R.;Henkelman,G.J.Comput. Chem.2007,28,899.

(99) Maseras,F.;Morokuma,K.Chem.Phys.Lett.1992,195,500.

September 13,2011;Revised:October 25,2011;Published on Web:October 31,2011.*

.Email:chenfeiwu@ustb.edu.cn;Tel:+86-10-62332689.

Comparison of Computational Methods for Atomic Charges

LU Tian CHEN Fei-Wu*
(School of Chemical and Biological Engineering,University of Science and Technology Beijing,Beijing 100083,P.R.China)

Atomic charge is one of the simplest and the most intuitive description of charge distribution in chemical systems.It has great significance in theory and in practical applications.In this article we introduce the basic principles and special characteristics of twelve important computational methods for the determination of atomic charges and compare their pros and cons from various aspects by considering a large number of instances.These methods include Mulliken,atomic orbitals in molecules(AOIM), Hirshfeld,atomic dipole moment corrected Hirshfeld population(ADCH),natural population analysis(NPA), Merz-Kollmann(MK),atom in molecules(AIM),Merck molecular force field 94(MMFF94),AM1-BCC, Gasteiger,charge model 2(CM2),and charge equilibration(QEq).Finally some general suggestions on how to choose a proper method for practical applications are given.

Atomic charge;Computational chemistry;Population analysis;Electronegativity; Electrostatic potential

10.3866/PKU.WHXB2012281

The project was supported by the National Natural Science Foundation of China(20773011).

国家自然科学基金(20773011)资助项目

O641