基于神经网络的变位储油罐罐容表标定

李 彬，周 斌，李国平

（湖南工学院，湖南 衡阳421002）

通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进／出油量与罐内油位高度等数据.通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，可得到罐内油位高度和储油量的变化情况.

但许多储油罐在使用一段时间后，由于地基变形等原因，罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变.因此，加油站需要定期对罐容表进行重新标定［1］.

1 问题的提出

本文将针对文献［1］所提供的实际储油罐尺寸及形状，以及相关检测数据等，对该储油罐罐容表进行重新标定.储油罐尺寸及形状如图1所示，该储油罐总容量V总＝32 332L.

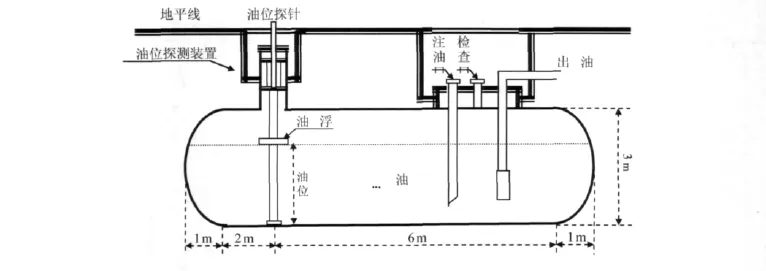
图1 储油罐示意图

到目前为止，对该问题的研究已经很多.大多数的研究是通过一定的近似处理手段，建立储油量V与显 示油高h以及变位角度之间的近似函数关系，最终转化为最优化问题来求解变位参数，从而得以修正罐容表［2－6］.

但现实中的储油罐罐体可能不是标准的几何体，而且储油罐内部还有很多小的仪器设备等，再加上储油罐横向、纵向倾斜，这几个方面都将导致计算储油量V与显示油高h之间的函数关系V＝V（h）比较困难；若要通过近似手段简化它们之间的函数关系，又会产生截断误差，从而导致结果不够精确.由于以上原因，本文将避免计算它们的函数关系，而采用径向基神经网络对函数V＝V（h）进行逼近，以修正罐容表.

2 问题的求解

2.1 径向基神经网络Ⅰ

建立径向基神经网络Ⅰ逼近函数V′＝V′（h），其中h为显示油高，V′为累积出油量.本步骤仅对文献［1］中一次性补充进油前的部分数据（流水号1≤i≤302）进行操作.

2.1.1 径向基神经网络Ⅰ训练集

文献［1］提供的实验数据有显示油高hi、出油量di（其中i为流水号，hi为显示油高第i个数据，di为出油量第i个数据，以下同）.显示油高与出油量尚不构成函数关系，可适当进行转换.根据，计算出累积出油量数据Vi′，如表1所示.

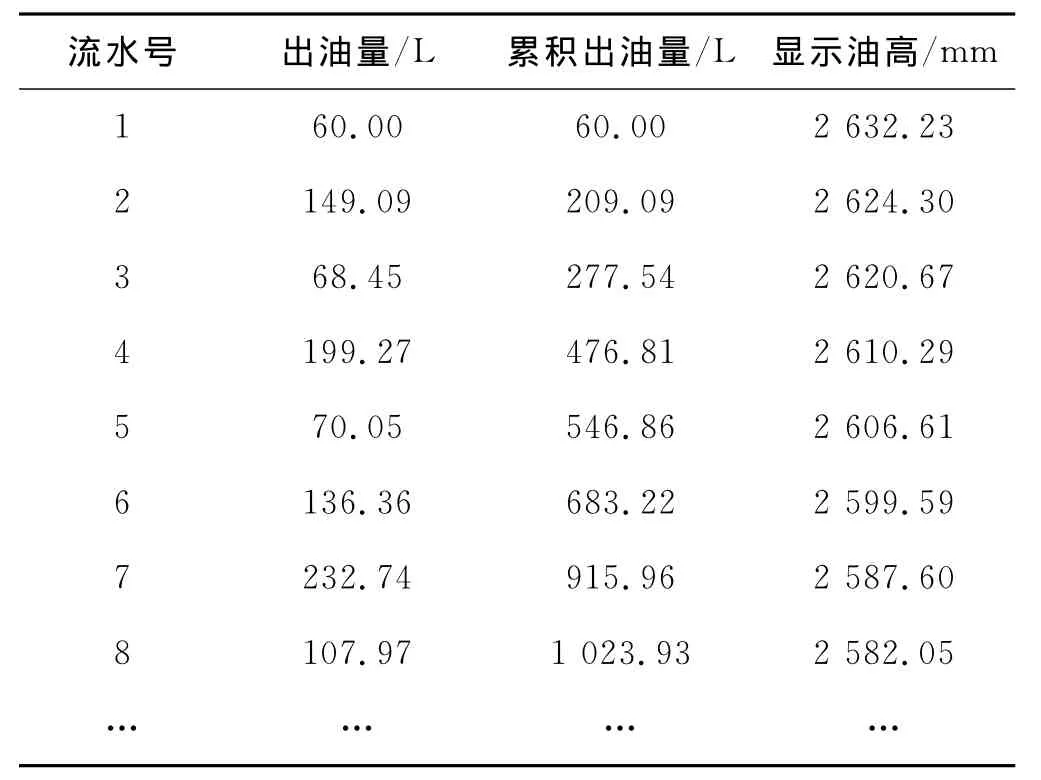
表1 显示油高与累积出油量对应表

2.1.2 径向基神经网络Ⅰ训练与仿真

利用以上所得训练集对径向基神经网络Ⅰ进行训练.用训练好的径向基神经网络Ⅰ进行仿真，取0.5m≤h≤2.5m，步长0.1mm，得出其对应累积出油量数据.

2.1.3 第一组累积出油量、储油量对应数据的获取

由于实验数据中无储油量数据，该数据的获取对问题的解决比较关键.通过获取第一组累积出油量、储油量对应数据，再利用公式计算出其他储油量数据.

第一组累积出油量、储油量对应数据通过以下步骤获得：

第二步：此时h＝1 575.65mm，V＝16 166L.取h＝1 575.65mm，对径向基神经网络Ⅰ仿真，得到V′＝26 625.46L，从而得到第一组累积出油量、储油量对应数据.

2.2 径向基神经网络Ⅱ

建立径向基神经网络Ⅱ逼近函数V＝V（h），其中V为储油量.

2.2.1 径向基神经网络Ⅱ训练集

根据以上所得第一组累积出油量、储油量对应数据，以及公式Vi＝Vi＋1－di＋1＝Vi＋1－（Vi＋1′－Vi′），计算出所有与Vi′对应之Vi，结果如表2所示.其中Vi为储油量第i个数据.

表2 显示油高与储油量对应表

2.2.2 径向基神经网络Ⅱ训练仿真与误差检验

首先利用以上所得神经网络Ⅱ训练集对神经网络Ⅱ进行训练，再利用文献［1］中一次性补充进油后的部分数据（流水号305≤i≤588），对径向基神经网络Ⅱ进行仿真，得出理论出油量、理论累积出油量等，并与实际值进行比较，结果如表3所示.出油量误差的标准值为1.001 8L，累积出油量误差的标准值为0.769 4 L，可见大批量采油误差更小.

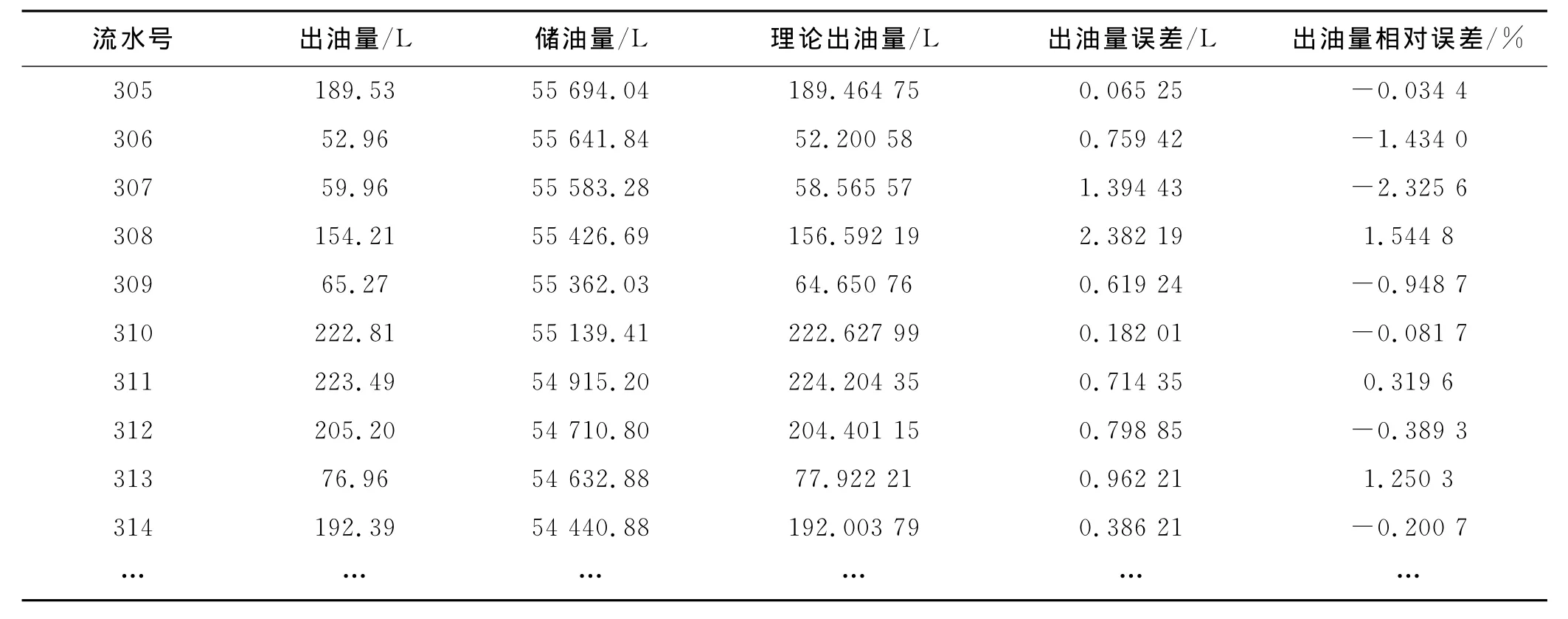
表3 出油量误差表

3 灵敏度分析及罐容表的重新标定

3.1 灵敏度分析

由于文献［1］中出油量、显示油高等实验数据可能存在误差，通过对出油量、显示油高等数据进行随机扰动来模拟实验数据中可能存在的误差，检验其结果是否稳定.

假设单次出油量误差在1L以内，显示油高误差在1mm以内（实际储油罐刻度精确到0.1mm），出油量、显示油高等数据误差符合正态分布.根据“3σ原则”，可取显示油高误差Δh～N（0，0.332），出油量误差Δd～N（0，0.332）.随机扰动后，重新进行神经网络训练与仿真，得到其误差，如表4所示.出油量误差的标准值为1.001 7L，累积出油量误差的标准值为0.766 9L，模型结果很稳定，和扰动前几乎无差异，甚至扰动后比扰动前误差更小了，这也正好从一个侧面说明了实验数据确实是有误差的.

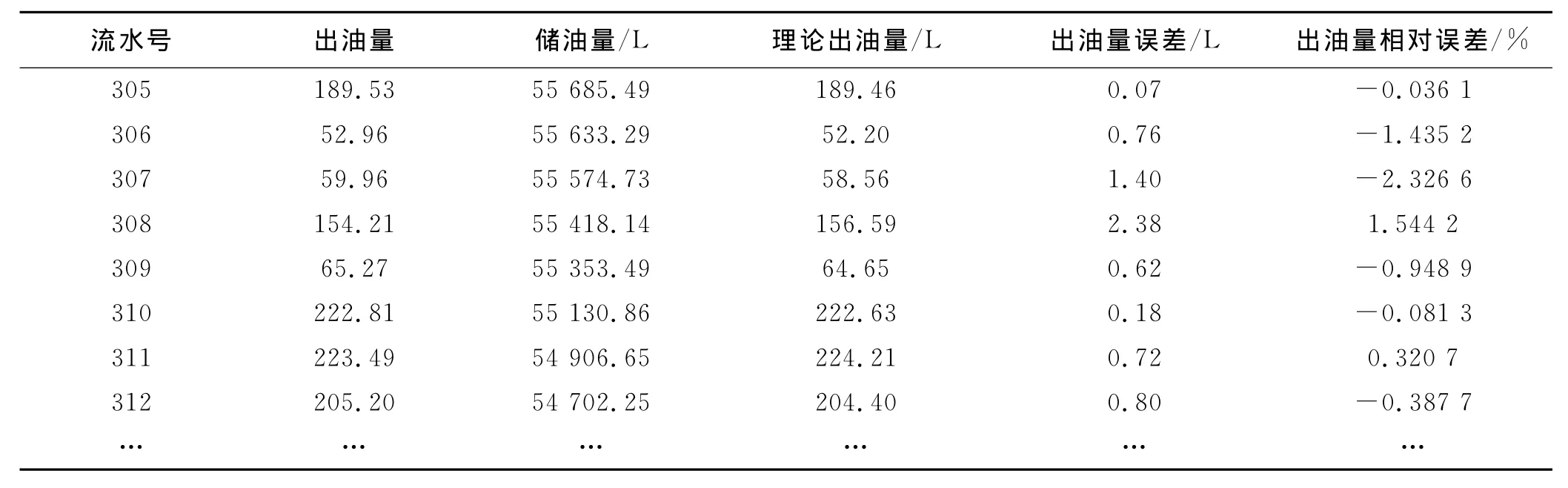
表4 扰动后出油量误差表

3.2 罐容表的重新标定

取0.5m≤h≤2.5m，步长0.1mm，对径向基神经网络Ⅱ进行仿真，得到修正后的罐容表，结果如表5所示.

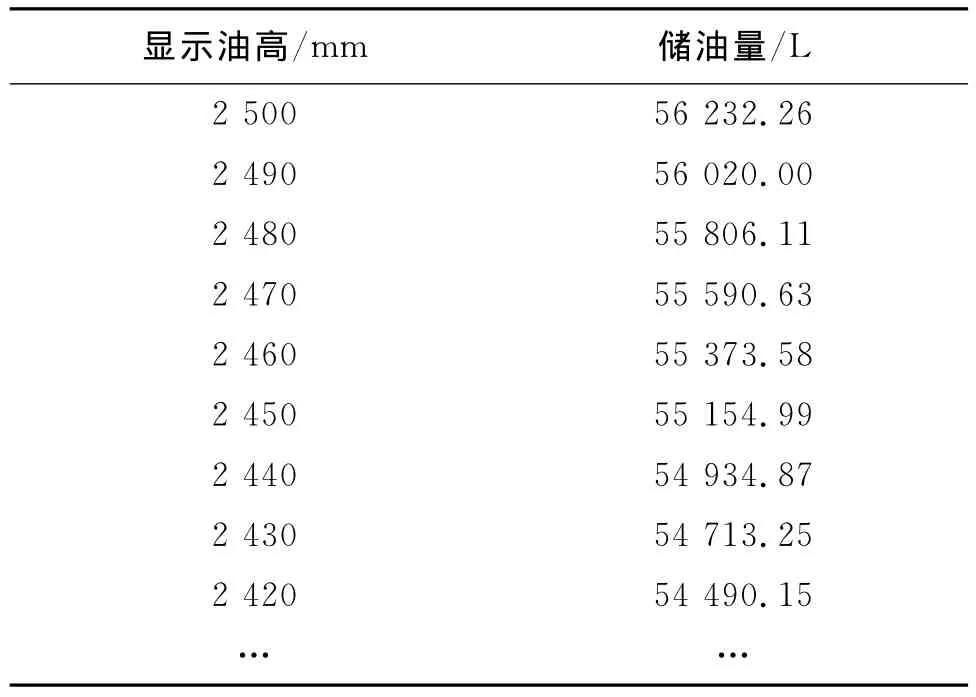
表5 修正后的罐容表

4 结 语

利用径向基神经网络数学模型，修正了变位储油罐罐容表；通过实验数据随机扰动，对模型灵敏性进行了检验，检验效果较理想，模型结果稳定.

［1］中国工业与应用数学学会.2010年全国大学生数学建模竞赛［EB／0L］.（2010－09－17）.http：／／www.mcm.edu.cn／html／cn／block／8579f5fce999cdc896f78bca5d4f8237.html.

［2］窦霁虹，梅钰，陈振勋，等.储油罐的变位识别与罐容表标定模型［J］.纯粹数学与应用数学，2011（6）：829－840.

［3］李玥姮，折波，惠宝军，等.基于修正积分模型的油量表重新标定与储油罐变位识别的研究［J］.纯粹数学与应用数学，2011（8）：562－568.

［4］朱毅鑫，裴静文，陈磊.储油罐变位识别与罐容表标定问题的研究［J］.纯粹数学与应用数学，2011（8）：556－561.

［5］王国领，刘扬，肖法沛，等.储油罐变位识别与罐容表标定方法［J］.武汉理工大学学报（信息与管理工程版），2011（8）：594－597.

［6］葛立，张玉洁，王磊，等.储油罐变位识别与罐容表标定问题的探索［J］.河南科技学院学报，2011（12）：58－64.

［7］李彬，周斌，李国平.储油罐的变位识别与罐容表标定［J］.湖南工学院学报，2011（12）：51－55.