电磁线圈的动态电磁关系分析及应用

程 敏，白会涛，潘 勇

（1.中原工学院信息商务学院，郑州451191；2.郑州宇通重工有限公司，郑州450051；3.河南机电职业学院，郑州451191）

电磁线圈的动态电磁关系一方面可以保证磁力机械产品顺利工作，另一方面又影响该类机械产品的工作性能［1］.郑水英等在研究电磁阻尼器被动减振时，考虑了动态电磁关系产生的波动电流对阻尼器减振特性的影响，得出理论值与实验值吻合良好的结论［2］.李慧敏等在研究电磁辅助支撑的支撑特性时，将电磁线圈的动态电磁关系引起的感应电流引入到理论模型中，较好地解释了实验中支撑参数理论值与实验值之间存在误差的现象［3］.以上研究表明，电磁线圈的动态电磁关系对机械产品工作性能的影响不容忽视.但是，目前对电磁线圈的动态电磁关系的研究仅是针对某一机械产品，研究内容相对分散，很少有人对其进行系统的分析.

本文通过对不同情况下电磁线圈的感应电动势和动态阻抗的分析，得到了因励磁电流和间隙变化而产生的感应电流表达式，并对其合理性进行了分析与讨论.最后将动态电磁关系应用到机械系统变刚度电磁支撑装置中，得到了不同情况下电磁支撑装置的附加支撑刚度参数和附加阻尼参数的表达式，合理解释了电磁支撑装置在实验中存在附加刚度和阻尼参数的现象.

1 电磁线圈中的感应电动势

从结构和工作原理上来讲，磁力机械产品都可以看成电磁铁或按一定空间布置的电磁铁对.电磁铁是一种利用电磁感应原理，使通电铁心线圈中产生电磁力，从而吸引衔铁进行工作的一种执行器.事实上，电磁线圈是一个非线性电感元器件，当磁路的磁通发生变化时，电磁线圈中会产生感应电动势.对于组成闭合电路的电磁线圈而言，同时会产生感应电流，这符合法拉第电磁感应定律的要求［4］.当电磁铁线圈中的磁通Ф0随时间t发生变化时，在线圈中产生的感应电动势为：

式中：N为电磁铁线圈的总匝数.假定电磁铁铁芯、衔铁和间隙中的磁场是分段均匀的，在忽略漏磁和磁滞影响的情况下，根据磁路安培环路定律，线圈中的磁通势为［5］：

式中：μ0为空气磁导率，μ0＝4π×10－7H／m；S为磁场的有效面积；I为电磁铁线圈的电流（A）；G为电磁铁磁极与衔铁的间隙（m）.

由式（2）可知，对于结构参数一定的电磁铁来说，影响线圈磁通变化的因素主要有2个：一是励磁电流I；二是间隙G.因此可从以下3种情况来考虑线圈的感应电动势：

（1）第一种情况：励磁电流为交变电流，间隙为静态间隙.此时

将式（3）代入式（1），可得

其中，dI／dt称为电流变化率，表征电流变化的速度，与电流的变化频率有关.

（2）第二种情况：励磁电流为稳恒电流，间隙为动态间隙.此时

同理，将式（5）代入式（1），可得

其中，dG／dt称为位移变化率，反映了电磁铁间隙变化的速度.

（3）第三种情况：励磁电流为交变电流，间隙为动态间隙.此时

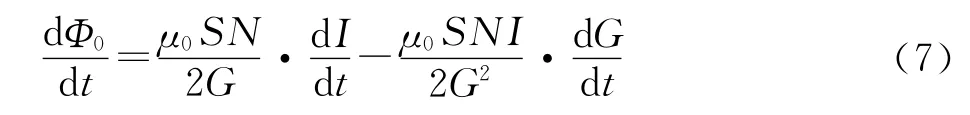
同理，将式（7）代入式（1），可得

2 电磁线圈的动态阻抗

电磁线圈的等效电路图如图1所示.

图1 电磁线圈等效电路图

图1中Rr为电磁线圈的电阻；L为电磁线圈的电感.在电路中，对于直流励磁电流来说，电感不起阻抗作用；对于交变电流来说，电感起到阻止电流变化的作用.下面分2种情况加以说明：

（1）当线圈中的电流为交变电流时，电磁铁的磁阻为［5］：

则电磁线圈的电感系数为：

式（10）表明：当电磁铁结构参数一定时，线圈的电感系数是一个常数；而当电磁铁的间隙发生变化时，线圈的电感系数将随之发生变化.

线圈中因交变励磁电流而产生的感抗为：

式中：ω为交变电流变化的频率（Hz）.此时线圈中的阻抗为：

（2）当线圈中的励磁电流为稳恒电流时，电磁线圈相当于一条导线，而非电感元件.此时，线圈中的阻抗为

3 电路中的感应电流

线圈中产生感应电流的条件是：①闭合回路；②磁通发生变化.对于电磁线圈来说，其满足产生感应电流的这2个基本条件.在计算感应电流时，特作如下假设：①忽略感应电动势和阻抗的相位差，即认为二者同相位；②忽略感应电流再次引起的电磁感应现象.

下面根据磁通发生变化的不同情况来讨论线圈中的感应电流：

（1）第一种情况：电流为交变电流，间隙为静态间隙.根据式（4）和式（12）可得

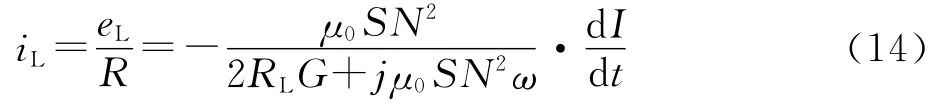
（2）第二种情况：电流为稳恒电流，间隙为动态间隙.根据式（6）和式（13）可得

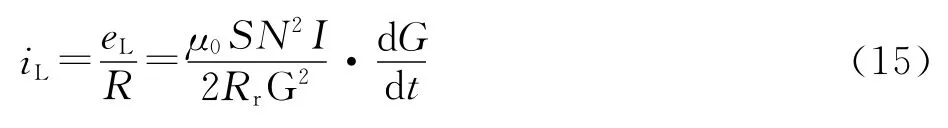
（3）第三种情况：电流为交变电流，间隙为动态间隙.根据式（8）和式（12）可得

4 分析与讨论

下面分析各种情况下所得感应电流表达式的合理性［6］：

（1）在第一种情况下，电磁线圈中只有因交变电流而产生的感应电动势，称为电磁线圈的自感现象.自感现象是电磁感应的特例，所以自感现象遵循所有的电磁感应规律.自感电动势仅能减缓原电流的变化，不会阻止原电流的变化或逆转原电流的变化趋势；原电流最终还是要增加到稳定值或减小到零［4］.由此可知，感应电流在数值上应小于原电流，即∣iL∣＜∣I∣.假设交变电流I＝I0ejωt，I0为电流幅值.将该交变电流对时间t进行求导，带入式（14），再进行取模运算，发现∣iL∣＜∣I∣恒成立.

（2）第二种情况反映了动态间隙对稳恒电流的影响.但此时存在这样一个问题，即对于稳恒励磁电流来说，电感将不起作用，仅相当于一条导线.因此，有人认为直流电磁铁的励磁电流仅与线圈电阻有关，不因间隙的大小而改变.但是，由式（6）可知，随着间隙的变化，磁路的磁通也发生变化，进而在闭合电路中产生感应电流，即间隙的变化将影响励磁电流的大小，这样就产生了矛盾.事实上，由对电磁辅助支撑和电磁阻尼器的相关研究可知，间隙的变化将导致励磁电流发生变化.为解决这一矛盾，可做一个关于动态间隙影响稳恒励磁电流的实验.通过实验可发现，此种情况下线圈中的确存在感应电流.

（3）在第三种情况下，感应电流表达式并不是前两种情况的线性叠加，而是受到交变电流和动态间隙两因素的交叉影响.这是因为线圈中存在的动态阻抗影响因动态间隙而产生的感应电流.事实上，电磁线圈的电磁关系是一种反复变化的动态关系.例如，由交变电流和动态间隙引起的感应电流又会反过来影响感应电动势，从而再次影响感应电流，并依次进行下去.但由于再次引起的感应电流与励磁电流相比非常小，可忽略不计.另外，在第二种情况下，由动态间隙引起的感应电流会在线圈中产生一个动态感抗，但是这个动态感抗远远小于由动态励磁电流引起的感抗.因此，在计算电磁线圈的阻抗时忽略了它的影响.其他两种情况也存在类似问题.

5 应用实例

利用电磁能进行工作的机械产品有很多.第一作者基于电、磁、力三者之间的依存关系设计了一种用于机械系统变刚度支撑的电磁支撑装置［7］，主要由电流源、电磁铁、衔铁和机械弹性元件组成，其结构示意图如图2所示.电流源是电磁支撑的控制源，控制电磁铁的磁场强度和电磁力，进而控制电磁支撑装置的支撑刚度参数.电磁铁由2块铁芯共用1块衔铁，呈对称分布，是整个支撑系统的执行部件.铁芯与机架的初始间隙均为g，并通入相同的励磁电流I，以保证电磁支撑的电磁力与动态间隙呈线性关系.机械弹性元件与机座相连，组成机械支撑装置，可以保证整个支撑系统在稳定区域内工作.衔铁为铁磁性材料，由机械支撑装置和电磁支撑装置并联组成的支撑系统支撑.

图2 机械系统变刚度电磁支撑装置的结构示意图

由图2可知，当衔铁沿X方向的位移为x时，上下电磁铁的间隙由g 变为（g＋x）和（g－x），且0≤x≤g.其中，g为静态间隙；x为动态间隙.此时电磁支撑装置的稳定悬浮状态被打破，电磁铁将沿X方向表现出吸力特性.

如果考虑动态电磁关系对磁路磁通的影响，电磁线圈中会产生感应电流，分别记为iL1和iL2.此时，电磁支撑的电磁力为：其中，λ是当考虑间隙处磁通不均匀分布而产生误差时加上的修正系数［8］，λ＝（1＋0.1ag）－1，a＝3～5.

将式（17）在x＝0，iL1＝0，iL2＝0处进行泰勒展开，略去高阶小项可得

由式（18）可知，如果忽略感应电流的影响，电磁力仅仅是位移x的一次函数.此时可得电磁支撑装置的支撑刚度参数为：

当电磁支撑装置的励磁电流为稳恒电流时，根据式（15）可得

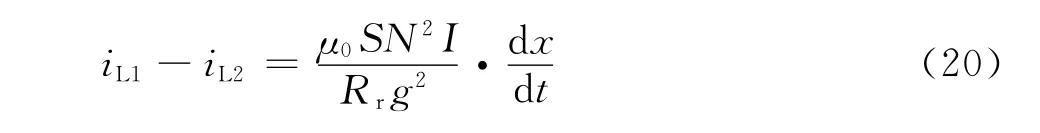
把式（20）代入式（18），可得

式中：

由此可知，当考虑动态间隙对电磁支撑装置支撑特性的影响时，电磁支撑装置在提供支撑刚度参数K的同时，还提供一个附加阻尼参数C′，这有利于整个机械系统的稳定.

同理，当励磁电流为交变电流时，根据式（16）可得

将式（23）代入式（18），可得此种情况下电磁支撑的电磁力表达式：

其中：

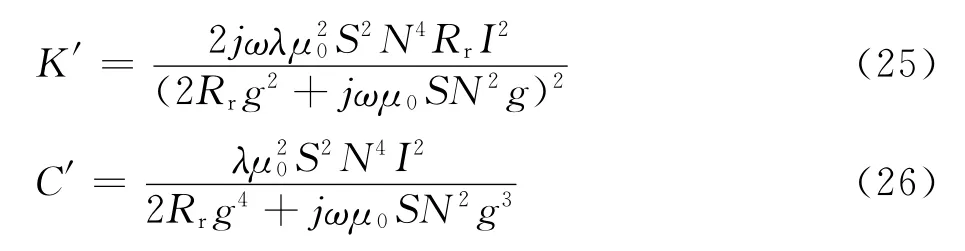
由上可知，当同时考虑交变电流和动态间隙产生的电磁感应时，电磁支撑装置的支撑特性将发生明显变化，同时产生附加支撑刚度和阻尼参数.附加支撑刚度和阻尼参数有利于整个支撑系统的稳定，这也在某种程度上使得电磁类机械产品具有一定的稳定性.

另外，通过搭建悬臂梁实验装置对电磁支撑装置的支撑参数进行实验识别，结果表明，当考虑动态间隙对电磁支撑装置支撑特性的影响时，支撑系统中的确存在附加阻尼参数，从而解释了电磁支撑装置支撑参数理论识别值与实验识别值之间存在差异的现象［7］，进而有力地证明了电磁线圈的动态关系对电磁类机械产品工作性能的影响是不容忽视的.

6 结 语

动态电磁关系是磁力机械产品顺利工作的前提和基础.本文通过研究影响动态电磁关系的电流和间隙参数，得到了表征动态电磁特性的感应电动势和动态阻抗.忽略二者的相位差，即认为二者同相位，同时忽略感应电流再次引起的电磁感应现象，得到了不同情况下感应电流的表达式，并对其合理性进行了分析.最后将动态电磁关系应用到机械系统变刚度电磁支撑装置中，得到了不同情况下电磁支撑装置存在的附加支撑刚度参数和附加阻尼参数的表达式，合理解释了电磁支撑装置在实验中存在附加阻尼参数的现象，从而也为磁力机械产品的结构设计和工作参数的合理确定提供了理论依据.

［1］赵韩，田杰.磁力机械学［M］.北京：高等教育出版社，2009.

［2］郑水英，马振飞.被动式电磁阻尼器的原理与实验研究［J］.振动工程学报，2005，18（1）：75－78.

［3］李慧敏，曾胜，汪希萱.电磁辅助支承的被动式减振研究［J］.中国机械工程，2003，14（24）：2087－2089.

［4］赵凯华，陈熙谋.电磁学（第二版）［M］.北京：高等教育出版社，1985.

［5］邹继武，刘宝廷，崔淑梅，等.磁路与磁场［M］.哈尔滨：哈尔滨工业大学出版社，1998.

［6］程敏.旋转机械随机支撑刚度参数模拟试验装置的设计研究［D］.郑州：河南工业大学，2010.

［7］程敏，潘勇，刘保国，等.用于机械系统变刚度支撑的电磁支撑研究［J］.中国机械工程，2011，22（15）：1862－1866.

［8］杨祚新.电磁铁应用设计计算方法［J］.机床电器，1996（1）：44－46.