基于二维云模型的复杂电磁环境下雷达作战能力仿真评估
池建军,罗小明,王伟中,郭钰
(1.装备学院,北京101416;2.96211部队,云南 建水654308;3.91329部队,山东 威海264200)
1 引言
目前,雷达作战能力评价方法很少考虑指标之间的相关性,并伴有较多的主观判断因素,例如:层次分析法、综合评判法,不能体现指标间的关联性,导致所反映的装备整体状况并不准确。由于复杂电磁环境下雷达作战能力发挥存在很大的不确定性,所以从微观角度着手已很难把握宏观的整体涌现效果。为了解决这一问题,本文引入云理论将定量的数值与定性的语言判断结合起来界定复杂电磁环境与雷达作战能力之间的对应关系,并实现对复杂电磁环境下雷达作战能力的评估。
2 云理论
2.1 云的基本概念和数值特征
云是用语言值表示的某个定性概念与其定量值概念之间的不确定性转换模型,云的整体特性可用云的数字特征来反映,用期望值Ex、熵En和超熵He三个数值来表示,它把模糊性和随机性集成到一起,构成定性和定量相互间的映射。其中Ex是云的重心位置,标定了相应的定性概念的中心值,En是定性概念不确定性的度量,它的大小反映了在论域中可被定性概念接受的元素数,即亦此亦彼性的阈度。He是熵的不确定性的度量,即熵的熵,它反映了云的离散程度[1]。
例如,用云的概念来描述“雷达中等作战能力”这一定性的语言值。那么可以设Ex=0.5,En=0.1(根据概率论与数理统计学知识,Ex的左右各3En的范围内应覆盖99%的可被概念接受的元素),而He可大约赋值为0.03,通过正态云发生器可得到“雷达中等作战能力”的描述。
二维云的数字特征用期望值(Ex1,Ex2)、熵(En1,En2)、超熵(He1,He2)[2]表示。
(1)期望值(Ex1,Ex2):二维云覆盖范围下的X1OX2平面上投影面积的形心G(x1=Ex1,x2=Ex2),它反映了相应的由两个定性概念原子组合成的定性概念的信息中心值。
(2)熵(En1,En2):二维云在X1OY平面和X2OY平面上投影后的边缘曲线——期望曲线的熵。它反映了定性概念在坐标轴方向上的亦此亦彼性的阈度。由Ex1,En1和Ex2,En2的数字特征值,分别确定了X1OY和X2OY平面上具有正态分布形式的云期望曲线方程:
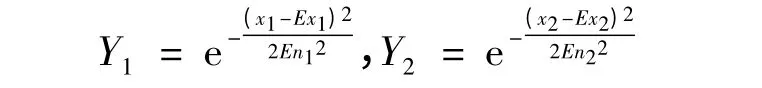
(3)超熵(He1,He2):He1或He2间接反映了二维云在这一平面上投影(一维云)的厚度,即其离散程度。
2.2 二维云发生器和二维云推理规则模型
云发生器是指被软件模块化或硬件固化了的云模型的生成算法模型。云发生器建立起定性和定量之间相互联系、相互依存,定性中有定量、定量中有定性的映射关系。由定性概念到定量表示的过程,是由云的数字特征产生云滴的具体实现,称为正向云发生器;由定量表示到定性概念的过程,是由云滴群得到云的数字特征的具体实现,称为逆向云发生器[3]。
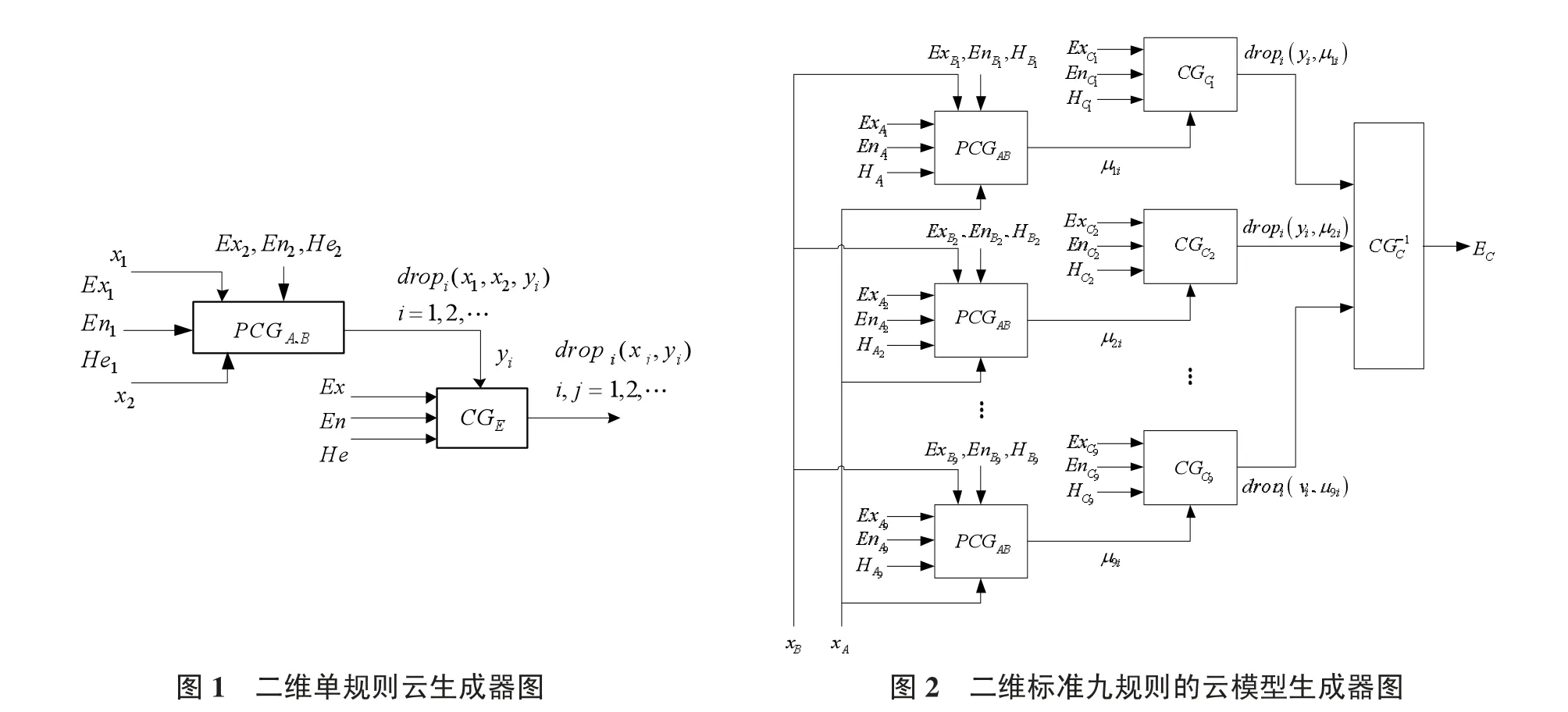
由各种云发生器可以组合起来构造规则生成器,可实现从一个定性概念到另一个定性概念的推理。利用二维X条件云发生器和一维Y条件云发生器可以构造一条复杂的定性规则生成器。比如规则IF A and B THEN C的云发生器,当确定了输入值,就将知道一个规律性的结果,如图1所示。
当多个这样的二维云单规则生成器组合起来作用时,就构成了二维多规则生成器,而且规则条件也可以是多个,如此就形成了复杂的推理机制,如图2所示。利用多规则生成器,就可以进行较高层次、较高难度的知识预测。
3 复杂电磁环境下雷达作战能力的云推理规则及云发生器
由于复杂电磁环境下雷达作战能力Cf取决于电磁环境空间的电磁干扰强度Pf和雷达抗电磁干扰能力Df两个基本因素。本文重点论述基于Pf和Df的复杂电磁环境下雷达作战能力云推理规则及云发生器。
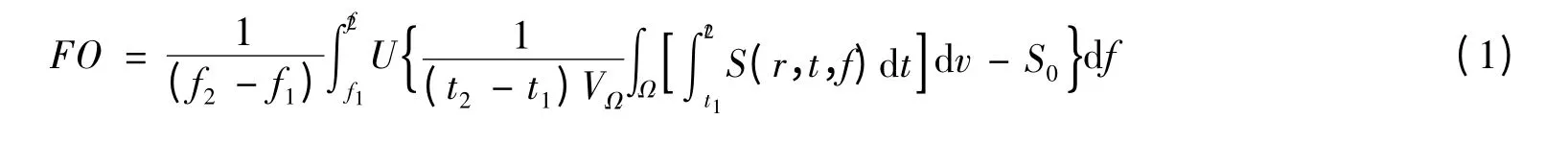
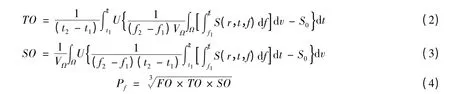
式中,FO为频谱占用度,TO为时间占有度,SO为空间覆盖率,f2-f1为用频范围,t2-t1为用频装备工作时间段,Ω为战场空间,U为单位阶跃函数,S(r,t,f)为功率密度谱,r为空间位置坐标,VΩ为作战空间体积,S0为电磁环境门限。
雷达的抗电磁干扰能力包括两部分:雷达的固有抗干扰能力和雷达作战使用的动态抗干扰能力。其中,固有抗干扰能力主要由雷达的战技性能、工作体制、抗干扰技术等构成;动态抗干扰能力主要由操控人员操控水平和经验、指挥员的指挥决策能力和电磁态势识别能力、各种战法的正确运用能力等组成。本文将如何定性分析雷达的抗电磁干扰能力这个问题进行专家咨询,设雷达抗电磁干扰能力Df可按表2中的等级规则描述。

表1 电磁干扰强度等级表

表2 雷达抗电磁干扰能力等级表

图3 电磁干扰强度等级云图
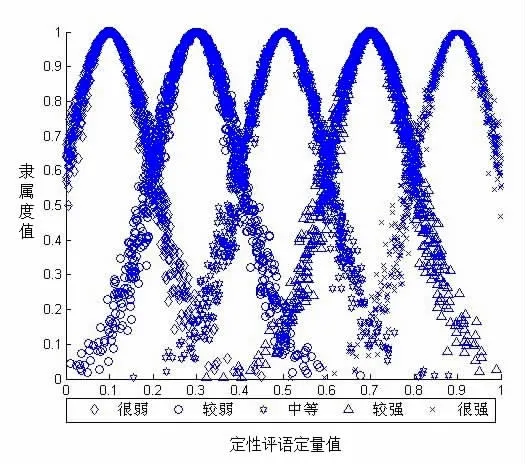
图4 雷达抗电磁干扰能力等级云图
将Pf、Df的等级用云来描述,如图3、图4所示。Pf和Df的每一个等级的定性描述都可以用一个正态云来拟合,横坐标表示定性评语对应的定量值,纵坐标表示每一个云滴对云的隶属度值。显然,云的最高点对应的横坐标值,即定性评语的期望值。
由此,如分析复杂电磁环境条件下雷达作战能力Cf=f(Pf,Df)就需要将表1和表2中的知识信息结合起来考虑。将表1和表2中的所有知识信息结合起来,会有5×5种关于复杂电磁环境条件下雷达作战能力推测的结果。但大多都具有随机性和模糊性,可以根据实际情况,利用能够掌握的历史资料信息,给出部分作战能力的推测结果,利用规则推理器的方法对其他情况下复杂电磁环境条件对雷达作战能力影响情况进行推理或预测。
本文总结出九条关于电磁干扰强度Pf和雷达抗电磁干扰能力Df共同作用体现的复杂电磁环境下雷达作战能力Cf之间的定性规则。将这九条规则列在表3中。

表3 复杂电磁环境下雷达作战能力定性评估九规则表
规则1:If E(电磁干扰强度很高)and等级3(抗干扰能力中等),then雷达作战能力很弱。
规则2:If C(电磁干扰强度中等)and等级5(抗干扰能力很弱),then雷达作战能力很弱。
规则3:If D(电磁干扰强度较高)and等级4(抗干扰能力较弱),then雷达作战能力弱。
规则4:If D(电磁干扰强度较高)and等级2(抗干扰能力较强),then雷达作战能力较弱。
规则5:If C(电磁干扰强度中等)and等级3(抗干扰能力中等),then雷达作战能力中等。
规则6:If B(电磁干扰强度较低)and等级4(抗干扰能力较弱),then雷达作战能力较强。
规则7:If B(电磁干扰强度较低)and等级2(抗干扰能力较强),then雷达作战能力强。
规则8:If A(电磁干扰强度很低)and等级3(抗干扰能力中等),then雷达作战能力很强。
规则9:If C(电磁干扰强度中等)and等级1(抗干扰能力很强),then雷达作战能力很强。
上述用于复杂电磁环境下雷达作战能力评估的9条定性规则,可通过图4所示的标准多规则控制器对象简单地映射过来,将一个定性分析问题以云模型为工具来进行定量分析。图4中,A表示电磁环境干扰强度;B表示雷达抗电磁干扰能力;C表示复杂电磁环境下雷达作战能力;xA表示电磁环境干扰强度值;xB表示雷达抗电磁干扰能力值;EC表示电磁环境对雷达作战能力的影响作用结果[2]。
完成这项工作还需要给出规则前件云(二维云)和规则后件云(一维云)的数字特征。数字特征可以根据历史数据以及数理统计原理综合确定,本文设数值特征如表4所列。
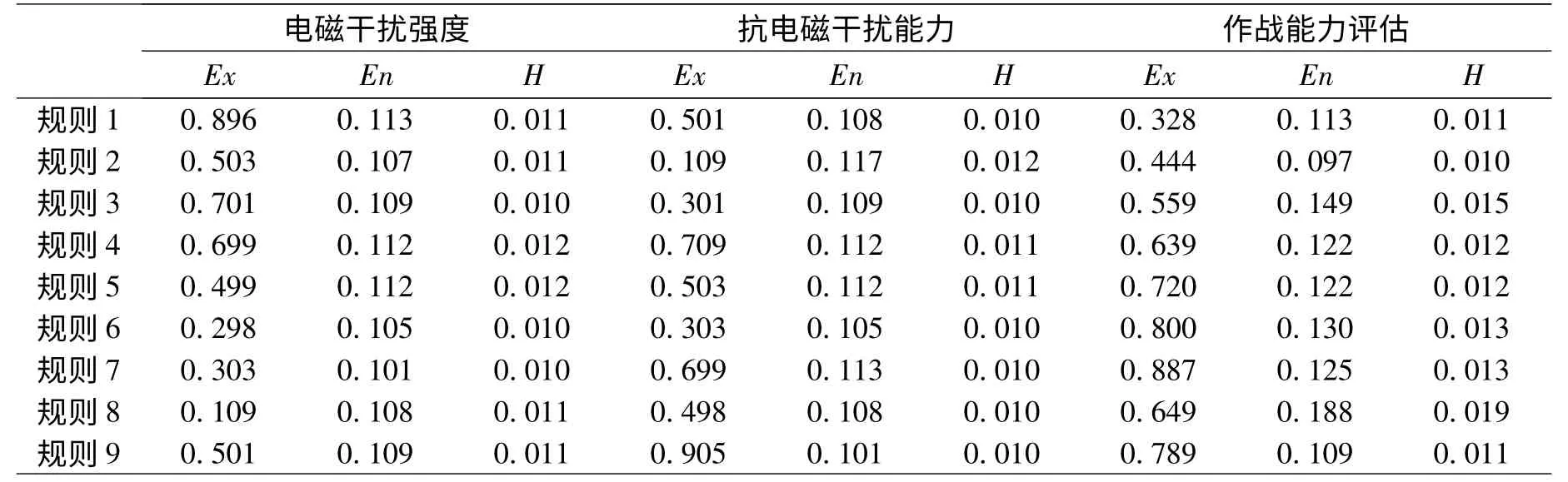
表4 复杂电磁环境下雷达作战能力评估云模型的数字特征参数表
4 复杂电磁环境下雷达作战能力评估的云模型算法
构造了复杂电磁环境下雷达作战能力评估的云规则发生器后,任意一条环境复杂性因素的相关信息都可以经过云规则发生器的处理,输出该条复杂性因素对雷达作战能力带来影响的评价。具体算法如下[3]:
(1)对每一条单规则,以(EnA,EnB)为期望、(HA,HB)为方差,生成符合二维正态分布的一个二维随机值(EnAj,EnBj)。式中:j=1,2,…,9。
(2)根据给定的输入:雷达所处电磁环境干扰强度Pf及作战能力Cf的数学期望值(xA,xB),由步骤(1)中的(EnAj,EnBj)求出由各个单规则生成器前件中输入(xA,xB)值所得到的激活强度,即隶属度μj:

(3)取μj中最大μj1和次大的μj2,则其相应的两条单规则被激活。分别根据这两条规则给定后件的(EnCk,HCk)随机生成以EnCk为期望,HCk为方差的一维正态随机值EnCk1、EnCk2,k取1~9中的某个值。
(4)根据公式(6),反计算求得在(μj1,EnCk1)条件下的两个yC1值和(μj2,EnCk2)条件下的两个yC2值(因为反计算中涉及开方,所以yC1、yC2值各有两个)。
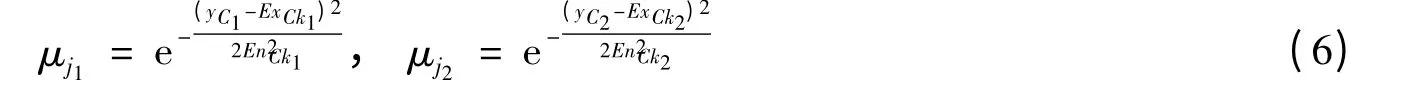
(5)各取两个yC1和yC2中的一个,它们的距离较之另外的yC1和yC2的距离要小。根据所取的两点(μj1,yC1)和(μj2,yC2),运用下面的方程,反计算出经过此两点的正态曲线的期望值ExC,亦可返回步骤(2),循环若干次,最终以所有期望值的平均值输出。

这个输出结果即是复杂电磁环境下的雷达作战能力评估值。通过该模型,可定量分析复杂电磁环境对雷达作战能力的影响。
(6)求取该值代表的定性语言结论。例如,给定用云模型实现复杂电磁环境下雷达作战能力评测的评语集:V=(v1,v2,…,v7)={很弱、弱、较弱、中等、较强、强、很强}。
设雷达常态下的作战能力为1,把7个评语置于连续的语言标尺上,并且每个评语值都用云模型来实现,就构成一个定性测评的云发生器,评语的数字特征如表5所列,云标尺中的云簇形成定性评语的激活区间,如图5所示。
将求得的作战能力定量值α输入测评云发生器中,同时制定阈值γ,如γ=0.1,则:激活某个评语云对象的程度远大于其他评语值(二者激活程度差值的绝对值大于给定的阈值γ)时,该评语即可作为对雷达作战能力的定性测评结果输出;若激活了两个评语值的云对象,且激活的程度相差不是很大(二者激活程度差值的绝对值小于某给定的阈值γ),则结果输出为该两个评语值。此时雷达作战能力的定性评估应介于这两个评语值之间,由用户再定义。

表5 定性评语集的云数字特征值表
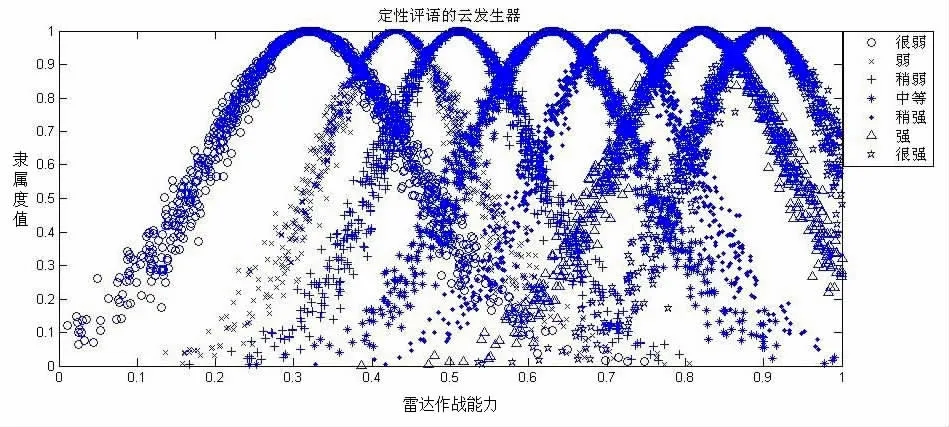
图5 作战能力大小定性语言值分布图
5 复杂电磁环境下雷达作战能力仿真评估实例
按照(1)~(6)步骤进行仿真计算,将电磁干扰强度Pf=0.5886和雷达抗干扰能力Df=0.7510输入模型,前件云和后件云的数字特征见表4。进行1000次仿真计算,得到云滴(yC1,μj1)、(yC2,μj2)和雷达作战能力生成的云滴各1000个。如图6所示,云滴相对集中在三个部分。通过计算雷达作战能力所有点横坐标的平均值,可得到雷达作战能力ExC,如图6中“☆”所示位置。将求得的作战能力定量值ExC=0.7017输入测评云发生器中,激活稍强评语云对象的程度大于其他评语值,即认为此时复杂电磁环境下雷达作战能力为稍强。
利用本文模型,对复杂电磁环境下不同电磁干扰强度下雷达作战能力进行仿真计算,数值如表6所列。得到雷达作战能力随复杂电磁环境干扰强度变化情况如图7所示。
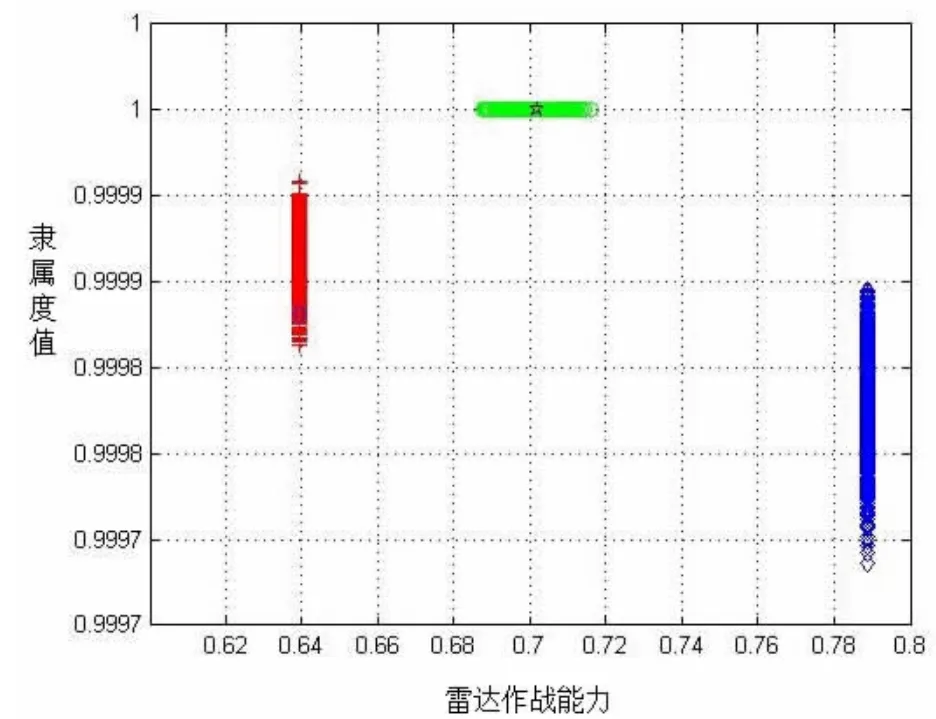
图6 (μj1,yC1)、(μj2,yC2)及雷达作战能力分布图
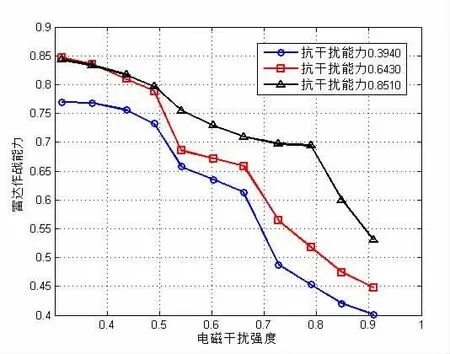
图7 雷达不同抗干扰能力下作战能力变化曲线图

表6 不同抗干扰能力下雷达作战能力值
从图9可以看出,随着电磁干扰强度的增加,雷达作战能力呈现不断下降的趋势,在同等电磁干扰强度下抗干扰能力强的雷达,其作战能力相对较高。图中雷达作战能力变化可分为三个态势:①干扰强度0.3~0.5:作战能力下降较平缓,②干扰强度0.5~0.7:作战能力下降幅度较大,③干扰强度0.7~0.9:作战能力急速下降,三种态势基本反映了雷达在不同电磁环境复杂等级中的工作状态。
1 李德毅.不确定性人工智能[M].北京:国防工业出版社,2005.
2 杨朝晖,李德毅.二维云模型及其在预测中的应用[J].计算机学报,1998,21(11):961-968.
3 吕彬.装备采办风险辨识与评估研究[D].北京:装备指挥技术学院,2006:57-66.
4 尹成友.战场电磁环境分类与分级方法研究[J].现代军事通信,2008,16(2):33-37.
5 古小明,周克胜,朱居莹.战场复杂电磁环境[J].四川兵工学报,2009,30(8):78-80.

