部队铁路输送路径选择算法研究

汪建伟，宋一丁，董立峰，贾斌

(1.军事交通学院，天津300161;2.总后后勤科学研究所，北京100071)

1 引言

目前，铁路输送仍是我军陆地防御和作战的一种主要远程机动方式，部队铁路输送方案编制的核心内容之一是确定输送路径。快速有效地选取最优路径对编制部队铁路输送方案具有重要意义。本文设计了以输送时间最短为目标的基于辅助的双向A*路径搜索算法，通过综合优化设计，使得算法中的路网数据减少，存储结构清晰，搜索范围缩小，计算速度加快，更符合快速编制部队铁路输送方案要求。

2 路网数据模型

路网是搜索最优路径的基础和对象，而要能够在路网上进行最优路径的搜索，必须将其转换为算法能够识别的信息，并以合理的结构组织和存储。

2.1 路网的表示方法

道路网络的经典表示方法是赋权有向图。通常是分别存储点状实体——节点、线状实体——两节点间的路段、节点和路段的属性信息，以及实体间的拓扑关系［1］(主要是连通性和方向性)。道路网的规模是影响最短路径搜索时间的主要因素，当在大规模路网上进行最优路径搜索时，如果将路网中的所有路段和结点平等对待，其计算量的庞大、搜索效率的低下是可想而知的。铁路路网的站点与一般网络中的节点不同，其中绝大部分站点只和2个站点关联，连接3个站点及更多站点的车站只不过占百分之十几。针对这种情况，本文采用了二次读入边数据的方法［2］来表示铁路路网。

(1)支点到支点的网络表示。首先忽略全部中间站点(连接两个边的站点)，形成一个简单的只有支点(连接三个及三个以上的站点)的网络。如图1(a)的网络可以简化为图1(b)所示的网络。如果要求计算从支点到支点的最短路径，那么在这个简化的网络上进行即可。

(2)中间站点到发的网络表示.如果出发站点是中间点，可以查询该站点至所在边两端站点的距离，暂时从网络中删除这条边，并增加1个站点Vk及2条边(Vk，Vi)和(Vk，Vj)，其边长分别等于从数据库读出的该站点距这2个支点的距离。

如果到达站点是中间点，那么处理方法同上。通过对铁路网络作了如上处理，全国路网即可表示成一个简化的网络，在这个网络上进行最短路径搜索其效率将得到明显的提高。

2.2 路网的存储结构

在确定了路网的表示方法之后，下一步的工作就是利用合理的数据结构将路网存储起来，使得路径选择算法能够识别路网，并在路网上进行最优路径的计算。衡量数据结构优劣的标准有两个:一是存储量小，冗余度小;二是便于路径选择算法操作。

铁路路网作为大型稀疏网络，具有很多特点。针对路网特点，由Dial等人提出目前公认的一种特别适合道路网络特点的存储结构——前向关联边结构［3］。该结构的核心在于将由同一个节点出发的所有弧存放在一起，在选择路径时可以避免一些不必要的判断。采用前向关联边存储结构，可以利用节点关联的弧段数目来控制循环次数，避开了大量不必要的循环运算。本文在此基础上结合实际需求对弧段权重进行了重排。

这种存储结构的一个明显好处在于使得路网数据结构更加清晰。前向关联边存储结构占用的存储空间少，还能方便地对某一给定节点发出的所有弧段进行操作，提高了算法的搜索效率。此外，通过对权重数组中各弧段的权值按大小进行排列，使得在路径搜索时不再需要比较弧段权重值，进一步提高了搜索速度。

3 路径选择算法的设计

3.1 基于辅助信息的双向A*搜索算法

图2所示为Dijkstra［4］、A*［5］及双向A* 三种最短路径算法搜索范围的比较，从图中可以看出双向A*搜索算法在搜索空间上较前两个算法减少了很多。双向A*搜索算法的时间复杂度为O)，其中b为网络结点的平均度数，d为从起点到终点最短路径搜索深度。由此可见，双向A*搜索算法无论从空间复杂度还是时间复杂度上都明显优于前两个算法。该算法的缺点在于复杂度较大，一般仅用于复杂的图形，而铁路路网就属于复杂的大型稀疏网络。

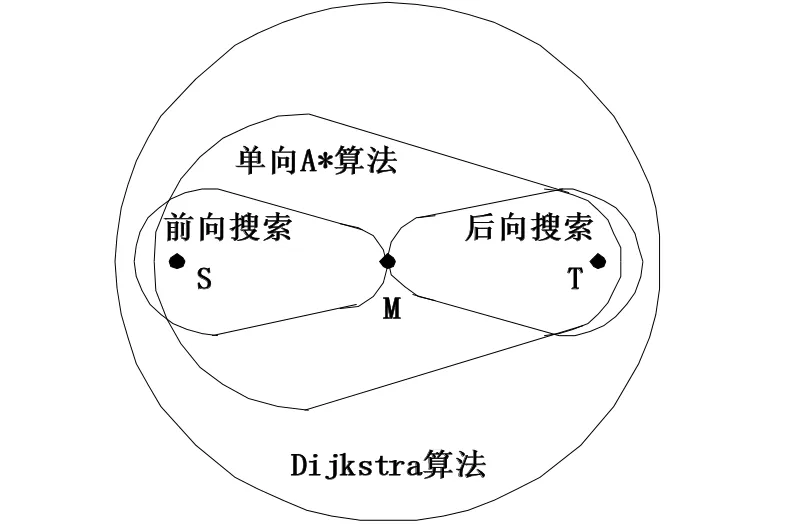
图2 算法搜索范围比较

在铁路运输中，当给定始发站和到达站后，列车可能通过路径的行政区域就确定了。例如列车从贵阳站开行至石家庄站，一般可能通过的行政区域包括贵州、重庆、陕西、山西、河南、湖南、湖北、山东和河北。根据铁路运输的这个特点，本文设计了用于限定搜索区域的辅助信息数据库。在扩展某一节点前，首先要判定该节点是否在限制的搜索区域之内。如果该节点在限制的搜索区域内则扩展之，否则，认为该节点不在最短路径上，不予考虑。算法利用知识来限定搜索区域，不仅缩小了算法的搜索范围，而且因为限制区域是给定的，不需要进行计算，也没有增加算法的复杂度。为了便于描述算法搜索过程，本文定义以下相关符号:x表示起始结点s或目标结点t，若x=s，则¯X=t，若x=t，则¯X=s;gx(n)是在状态空间中从结点x到当前节点n的实际代价;hx(n)从当前节点n到目标节点¯X最佳路径的估计代价;f=gx(n)+hx(n)是从初始点x经由节点n到目标点¯X的估价函数;x-OPEN由算法所扩展的结点集，等待进一步扩展;x-CLOSED由算法所扩展的且不在x-OPEN中的结点集。

改进后的双向A*搜索算法具体步骤如图3所示。

图3 改进的双向A*算法流程图

3.2 估值函数t(n)的设计

估值函数能否正确选取将直接关系到算法成功与否，而函数的确定却与实际情形密切相关。算法使用者可以依据实际情况，选择f(n)的具体形式。估值函数的估价值应与实际值尽量接近，这就要求启发函数h(n)的启发信息越多越好，即h(n)的值尽可能大，提高算法搜索效率。另一方面，为了保证算法的正确性，我们又需要适当地降低估价函数的值，扩大搜索范围。因而可以根据实际对求解速度和正确性的要求而设计出不同的估值函数，使之更具弹性。

对于路网中路径选择问题，已经确定输送时间最短为最优目标。输送时间一般由单梯队运行时间和部队输送进度两部分组成，故可定义部队从起始站点经过站点n到达终点输送时间的估值函数为:

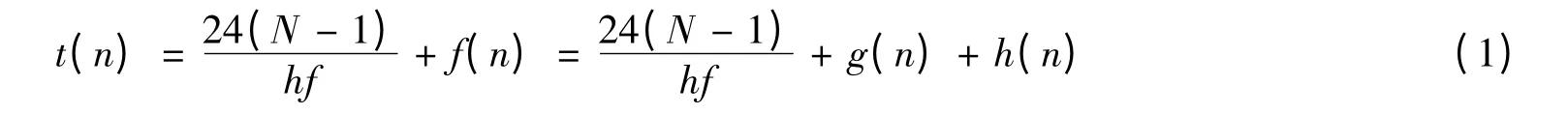
式(1)中，N为列车梯队数，h为当前已选路径中第一限制区段的通过能力，f为铁路线路军用占用率，g(n)为从起始站点到达当前站点n的输送时间实际代价函数，h(n)为当前站点n到达终点的输送时间启发函数。

式(2)中，wi为两车站之间区段长度，vi为列车在区段i上的运行速度。

式(3)中，D为两点间的直线距离计算公式，vmax为已选路径的区段中列车最大运行速度，β为常量系数，由辅助信息数据库提供。β值是这样确定的:假设某行政区域内相邻两站点实际距离为S实，直线距离为S直，行政区域内任意相邻站点实际距离与直线距离比值最小值就是该区域的常量系数，即βi=min

4 实验及结果分析

为验证改进的算法，本文绘制了部分铁路线路图(图4)，共包含87个站点和124条铁路区段，利用Java 6.0、Oracle 9i和Myeclipse 8.0作为实验环境，分别采用Dijkstra算法、A*算法、双向A*搜索算法和本文设计的基于辅助信息的双向A*搜索算法求解四对站点的最优路径。

各算法运行情况比较见表1。运行结果显示各算法都能找到最优路径，但各算法在搜索时间和遍历节点次数上存在着一定的差异。从表中可以看出，Dijkstra算法搜索时间是最长的，遍历节点次数也是最多的，因为该算法的搜索基本上是以起点为圆心以圆的方式向外拓展;A*算法从所搜时间和遍历节点次数两个方面都优于Dijkstra算法，但优势不是很明显，主要是给定的铁路线路图站点和线路区段数较少，没有充分发挥A*算法的特点;双向A*搜索算法在时间上优于前两个算法，但遍历节点次数却多于A*算法，这一方面是因为给定的铁路线路图相对简单，双向选择算法难以发挥优势，另一方面是因为我们在程序中凡有节点放入源点或目标点的OPEN表时算法计数均加1，一些点在实际搜索过程中并没有使用;本文设计的基于辅助信息的双向A*搜索算法，从搜索时间和遍历节点次数上相对前面的算法都是最少的，这充分证明了改进算法的先进性。

表1 四种算法的运行情况比较(时间单位:ms)

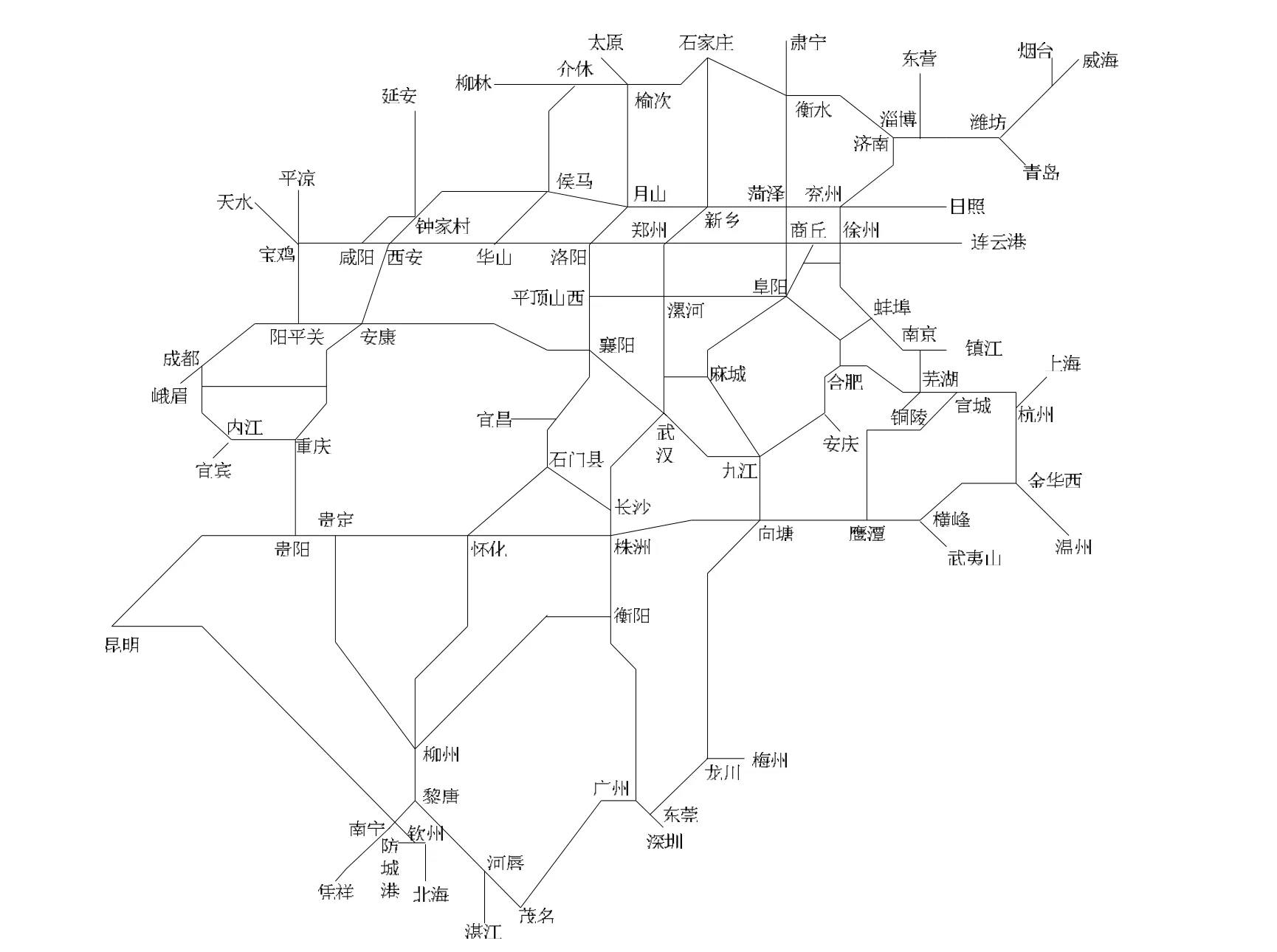
图4 铁路输送路径选择流程图

5 结语

本文从部队快速选择铁路输送最优路径的需求出发，根据铁路路网特点，从路网表示、存储结构、搜索区域、估值函数四个方面对双向A*路径搜索算法进行了优化，提高了搜索效率，具有较好的实用性，可以应用于路径选择相关的决策信息系统中。

1 夏立民.交通系统中最优路径选择算法的研究［D］.北京:首都大学，2007.

2 杨斌，魏佳.铁路超限货物最短运输径路查询系统的研究［J］.铁道运营技术，2010，16(2):1-7.

3 万玮，刘晔，李立宏，等.采用联合优化方式的最佳路径算法研究［J］.计算机工程与应用，2007，43(30):97-100.

4 DIJKSTRA E W.A Note on two Problems in Connexion with Graphs［J］.Numerische Math-ematik，1959(1):269-271.

5 HART E P，NILSSON N J，RAPHAEL B.A Formal basis for the Heuristic Dtermination of Minimum Cost Paths［C］.IEEE Trans.Sci.Cyhern，1968，SCC-4(2):100-107.