Application of the SWT Method to Scattering from Water-filled Elastic Spherical Shells

FAN Wei,FAN Jun,WANG Xin-ning

(School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

1 Introduction

The Sommerfeld-Watson Transformation method(SWT)is widely used in the field of acoustic or electromagnetic scattering computation,it can convert the slow convergence partial wave series to a fast convergent residue series.Many researchers have done a lot of research work on this subject.Nussenzveig gave a complete discussion about this topic and derived the relevant mathematical equations to acoustic scattering from impenetrable[1]and transparent[2-3]sphere.The use of SWT to the scattering of elastic cylinder was implemented by Doolittle[4]et al.Rumerman[5-6]applied the SWT to the scattering of acoustic waves obliquely incident upon cylindrical shells.Gaunaurd[7]analyzed the scattering from a submerged air-filled cylindrical steel shell coated with a viscoelastic layer through SWT.Moreover,a ray synthesis theory was developed from the SWT implement for the case of elastic sphere by Marston[8].In the process of carrying out the SWT,the numerical evaluation of Bessel and Hankel functions of complex order and real argument is inevitable.Paknys and Jackson[9]studied a variety of asymptotic expansions of cylindrical functions and used the SWT to explain the behaviors of complex waves.

Scattering of sound waves by evacuated elastic spherical shell has been studied by many authors over the years.Gaunaurd[10-11]analyzed the connection between internal resonances and the Lamb waves in a spherical shell when it is fluid-loaded.Überall[12]explained the feature of the dispersion curves of various of circumferential waves which take place on the evacuated spherical shells.Sammelmann and Hackman[13-15]used the resonance scattering theory[16]to study the scattering from a evacuated elastic spherical shell,and analyze the poles structure of the scattering amplitude in the complex frequency plane.They concluded that outer fluid loading has a profound effect on the vacuum dynamical characteristics of the shell.However,the water-filled elastic shells present more complicated backscattered echoes when compared to evacuated shells and are less well understood.The central objective of this paper is to apply the Sommerfeld-Watson transformation method to scattering from a water-filled spherical shell,and present resonance structure of the various types of circumferential waves on the frequency domain and wave-number domain,respectively.In order to give a comprehensive understanding of scattering mechanism for the water-filled spherical shell,the dispersion and attenuation curves are also discussed in this paper.

2 Modal solution and Sommerfeld-Watson Transformation

Fig.1 illustrates the scattering geometry.An elastic spherical shell of outer radius a and thickness h,respectively,is placed in an acoustic medium.The interior of the spherical shell is taken to be filled with water.The plane sound pressure field incident upon the shell can be expressed as Eq.(1).The wave number k of the incident plane wave is defined by k=ω/c,where ω is the angular frequency and c is the speed of sound in water.The harmonic time dependence exp（-jωt）has been suppressed.Pn（x）and jn（x）are the standard Legendre functions and spherical Bessel functions,respectively.

Fig.1 Geometry and notation for the spherical shell

The expansion of Eq.(1)is based upon the origin of the coordinate system being at the centre of the spherical shell.The variable r is the three-dimensional range,the variable θ is the polar angle measured off the vertical axis.According to the classical elastic theory,the steady-state scattering pressure in the backscattered direction has exact partial wave series representation:

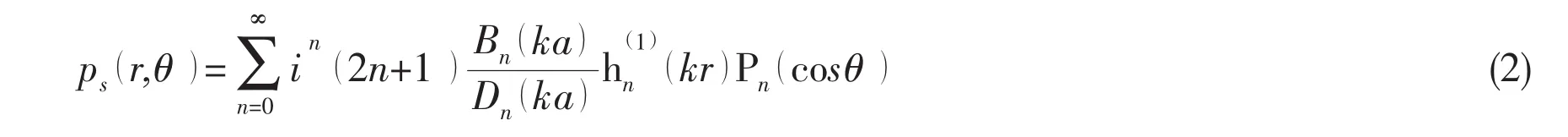
The continuity of displacements and stresses at the interfaces yields the necessary equations to determine all the 6×6 determinants Bn（ka）and Dn（ka）at each order n in Eq.(2).The elements of these determinants,which are complicated expressions of spherical Bessel functions and spherical Hankel functions of the first kind,can be found in Ref.[10].

It is well known that resonance frequencies are generated by the phase matching during circumferential propagation of surface waves around elastic shells.In other words,the circumferential wave can arrive at the receiver point only when the phase matching condition is satisfied,and it leads to a resonant build-up of circumferential waves.The complex resonance frequencies of submerged elastic body such as elastic cylinders,spheres and evacuated spherical shells are well studied in the Ref.[17].However,to the best of the author’s knowledge,the pole pattern of the water-filled elastic shell in the complex resonance frequency plane has not yet been given.To obtain that,the following dispersion eigenequation should be solved for each mode number n.

The zeros x=kla of Dn（x）define the discrete eigenfrequencies of water-filled spherical shell,which can be used to obtain individual points on the dispersion curves.However,the full property of circumferential waves around the shell can be acquired only in the wavenumber domain,in which various type of waves for each frequency point are discussed.Then continuous dispersion curves can be calculated for all frequency point,not only in the situation of resonance occurred.An effect method for solving the problem in wave number domain is SWT.The SWT begins with the transformation of the partial wave series into an integral.In order to perform this transformation,an analytical extension is made on the partial wave number n,which is replaced by the complex variable v,and the following relation[1]is used:

Substituting Eq.(2)into Eq.(4),and then deforming the integration contour so that the partial wave series in Eq.(2)is transformed into an integral on a contour that encloses physical singularities,and this integral can be evaluated by the residue method.As a result,the SWT synthesis of the scattering form function f which is defined by ps=（aeikr/2r）f may be written as the sum of two terms,as shown in Eq.(5):

where the specular reflection part fgeois evaluated by saddle-point methods,and the residue sum part fwavecorresponds to circumferential waves contribution.Their detailed derivation has been omitted here to save space,only the final expression is given:

The variables in Eq.(6)are defined as follows:xt=ωa/ct,βs=arccos（vs/ka）.The saddle point is vs=kacos（θ/2）.The dimension of determinantsandare all five,and they are minors of matrix Dn（x）.In Eq.(7),the singularities denoted by vlare solutions of the characteristic equation

where Dvis the analytic extension of the determinant Dn,and ka plays the role of the frequency parameter.The physical meaning of vlis wave number poles of circumferential waves.The phase velocity cphof circumferential waves are related to scattering resonance frequency and wave number by Eq.(9)and Eq.(10),respectively.

3 Solving transcendental equations on frequency and wave-number domain

The dispersion equations of Eq.(3)on the frequency domain and Eq.(8)on the complex wave-number domain are all transcendental equations on the complex plane.It is difficult to use ordinary root finding algorithms such as Newton-Raphson iteration method and secant approach to this equations.Both these approaches seem to have been devised primarily for finding the real roots.When non-real roots are needed,the more complex roots move out into the complex plane,the more the results are inaccurate.To solve this difficulty for the current issue,the winding number integral method[18]is carried out,and it is very effective to determinate all the roots of the complex dispersion equations.The present paper uses the winding number integral method to solve Eq.(3)and Eq.(8),and here summarize its basic principles as follows.

Assume f（z）is an analytic function over the region Ω on the complex z plane and suppose that f（z）has no poles inside the boundary∂Ω of Ω,and all the zeros ak,k=1,2,…,p are simple.Under this hypothesis,the winding number integral will lead to the following linear equations according the argument principle.

The dimension of Eq.(11)is integer p which is the number of roots in the region Ω,and it can be calculated using the relationship:

The problem of finding the roots akof analytic function f（z）has now reduced to that of finding p zeros of a p order polynomial.In practice,the first step of the winding number integral algorithm is carrying out at initial splitting of the searching region into rectangle sub-regions such that each sub-region contains no more than three roots.The performance of the winding number integral algorithm to the specific problem of acoustic scattering from a waterfilled elastic spherical shell will be validated by the following numerical calculation.It is worth noting that Eq.(3)contains special functionsandwhich are cylindrical functions of integer order n and complex argument z.There are many mathematical software or math packages provide the ability to compute this type of functions such as MATLAB and the numerical IMSL library in FORTRAN.However,to solve Eq.(8),it is indispensable to calculate the cylindrical functionsandwhere the order v is complex and the real argument x is nonnegative.Whether or not calculate these cylindrical functions accurately and rapidly on the interesting complex domain are critical to success of implementing the Sommerfeld-Watson transformation.Several numerical methods to this type of cylindrical functions have been mentioned in the mathematical literature such as direct numerical integration method,iterative method[19-20],differential equations method[21],asymptotic expansion method[22],etc.To overcome this problem,the present paper adopted the approach of Masao Kodama[23]to the research area of acoustic scattering.This method which is based on a series expansion,Debye’s asymptotic expansions,Olver’s asymptotic expansions,and Miller’s recurrence methods apply various asymptotic expansions expression according to their established range in different domain in the complex plane.

4 Numerical results and discussion

All subsequent numerical results are presented for the case of an aluminum spherical shell with a thickness to radius ratio h/a=0.05.The density of the aluminum spherical shell is ρs=2 710.0 kg/m3,the velocity of longitudinal wave and shear wave are cl=6 380.0 m/s and ct=3 120.0 m/s,respectively.The material properties of water are ρ=1 000.0 kg/m3,c=1 482.0 m/s.In this section,the pole structure of the scattering amplitude in the complex frequencyka plane is studied firstly.To obtain the pole locations of complex frequency,for each mode number n=0,1,2,3…,the root finding approach introduced above is carried out to Eq.(3)in the fourth quadrant of complex ka plane,and then collect all the poles in the same complex frequency-ka plane.

Figs.2(a)and(b)display the pole locations in the complex frequency-ka plane for empty and water-filled spherical shells,respectively.In the Fig.2(a),a0+and a0-represent the supersonic part and the subsonic part of the spherical lowest order antisymmetric Lamb waves,respectively.s0denotes the spherical lowest order symmetric Lamb wave.The results of Fig.2(a)agree well with Sammelmann’s calculation[13],however,that work is for scattering of evacuated spherical shells.Water-filled elastic shells present more complicated pole structure as shown in Fig.2(b).It is noted that the main differences between empty and water-filled,spherical shells are a large number of poles appeared below the real axis,and this additional poles occur due to internal fluid loading.

Fig.2 Complex resonance frequencies(a)Evacuated shell;(b)Water-filled shell,h=0.05a

The results of the resonance frequencies in Fig.2(b)can be used in Resonance Scattering Theory(RST)which reformulates the scattering amplitude for water-filled spherical shells in a way that explicitly shows the presence of resonance,however,it is not considered in the present paper.In order to represent the scattering pressure field in terms of wave number components for all frequencies,the complex wave number poles of circumferential waves should be calculated at first.For each dimensionless frequency ka,the winding number integral method is used to Eq.(8)in the first quadrant of the complex v plane.Figs.3(a)and(b)illustrate the distribution of the complex wave-number poles of circumference waves in the complex wave number v plane for water-filled and evacuated spherical shells respectively.The dimensionless frequency ka is selected as 50.0.It can be seen that considerable poles corresponding to fluid waves denoted as F0,F1,F2,F3,and so forth,arise due to internal fluid loading.Unlike in fre-quency domain,it is easy to identify each pole from each other in the complex wave number plane.The imaginary parts Im（vl）of each fluid wave pole vlindicate attenuation as a result of re-radiation from circumferential waves to the surrounding medium.

After obtaining the complex wave-numbers vlof circumferential waves for each frequency,the phase velocity dispersion curves for circumferential waves can be calculated from above poles results according to Eq.(10).Fig.4(a)shows the dispersion curves of a0-and the fluid waves propagating around a water-filled spherical shell.The phase velocity is normalized with respect to the sound speed in water and is plotted as a function of the normalized frequency ka,which range from 0.1 to 100.In order to point out the effects of inter-fluid loading on circumference waves of elastic shells,the dispersion curves corresponding to a0-,a0+and s0waves of evacuated shells are also plotted as a reference.The inter-fluid causes strong perturbation of the circumference waves structure for evacuated shells.Besides the a0-wave is basically unchanged,the a0+wave and s0wave are flooded with large amount of fluid waves.However,the influence of them is still obvious for the case of water-filled shells,an obvious feature of the curves displayed in Fig.4(a)is the repulsion of adjacent fluid waves of the water-filled spherical shell.The turning portions of the fluid waves curves seem to form a discontinuous dispersion curves of a0+wave and s0wave for evacuated shells.Another feature of Fig.4(a)is that,as the frequency increases,higher-order fluid circumference waves take place successively and their phase velocity decreases and tends to sound speed in water.

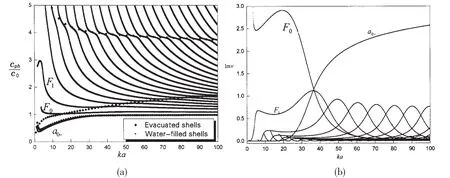
Fig.4 Water-filled elastic spherical shells(a)Phase velocity dispersion curves;(b)Attenuation curves

The attenuation coefficient Im（vl）is shown in Fig.4(b)as a function of the dimensional frequency ka.The behavior of the lowest order fluid wave and a0-wave is different from all other higher order fluid waves.As the frequency increases,the attenuation of a0-wave increases,and the attenuation of F0increases until it reaches a maximum,after which any further increase in the frequency results in a reduction in the attenuation and the attenuation coefficient eventually asymptotically goes to zero.

In order to study the attenuation of higher order fluid waves except for the lowset order fluid wave,a zoom of the region corresponding to higher order fluid waves is shown in Fig.5.It is interesting to point out that the attenuation curve for each higher order fluid wave in Fig.5 has two peaks in the frequency range of concern.Compare the dispersion curves and attenuation curves for fluid waves,it is shown that the maximum of attenuation is just at the frequency when repulsion phenomenon happens.Therefore,it is concluded that the ability of the fluid wave re-radiation to the surrounding medium is reaching local extremum when the phase velocity of fluid wave for the water-filled shell is close to that of a0+wave(Fig.5(a))or s0wave(Fig.5(b))for the evacuated shell.These results demonstrate the interaction bewteen the elastic spherical shell and internal fluid loading for the coupld fluid-shell system.

Fig.5 A zoom of attenuation curves for higher order fluid waves(a)a0+repulsion;(b)s0repulsion

The backscattering form function results by the Sommerfeld-Watson transform and the partial wave series method are given in Figs.6(a)and(b),for the case of empty and waterfilled,submerged spherical shells,respectively.From these figures,it can be seen very good agreement for backscattering form function f between the calculation of partial wave series and the SWT synthesis result.Generally,the partial wave series is summed with a minimum truncation constant of ka+5,which was selected to secure adequate convergence in the dimensionless frequency ka.It leads to expensive computational cost as the frequency increases.The SWT synthesis can convert the slow convergent partial wave series to a fast convergent residue series,which just includes the contributions to backscattering from the fluid waves,as well as the contributions from specular reflection and the a0-wave,for a water-filled spherical shell.As mentioned above,the amount of fluid waves increases for higher frequency,however,its growth rate is far less than the number of the summation terms for the partial wave series method.Figs.6(a)and(b)validate the accuracy of SWT method approach to scattering from water-filled spherical shells.

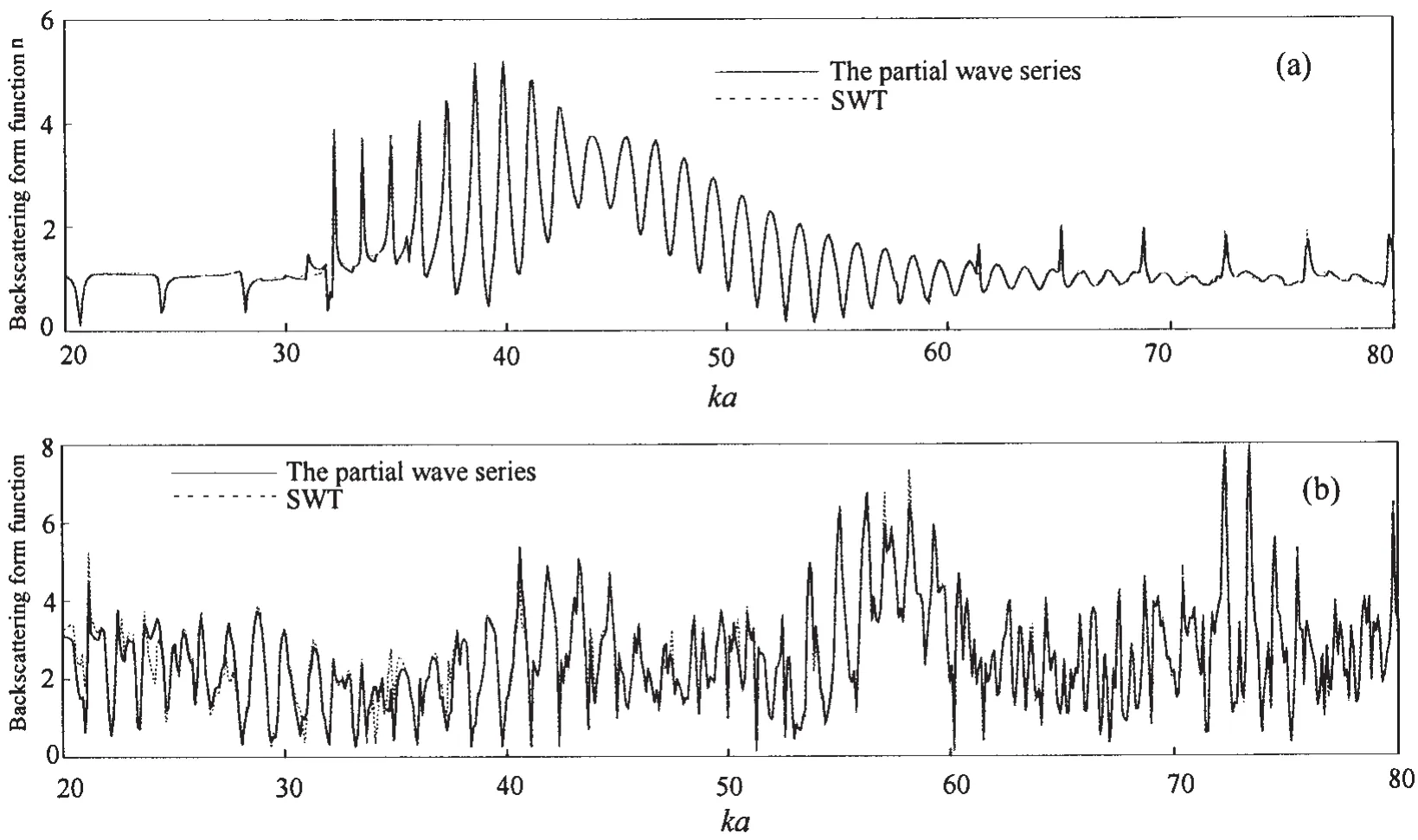
Fig.6 The partial series results and SWT synthesis results(a)Evacuated shells;(b)Water-filled shells

5 Conclusions

In this paper,we have discussed the scattering from water-filled elastic spherical shell using the method of Sommerfeld-Watson transformation.Firstly,the dispersion equations in the frequency domain and wave number domian are numerically solved using the winding integral method.Then,the phase velocity and attenuation curves of corresponding circumferential waves for evacuated and water-filled spherical shell are compared.The following conclusions can be drawn:

(1)The problem of numerical calculation of cylindrical function of complex order and real argument is overcomed by applying various asymptotic expansions expression in different domain in the complex plane.

(2)For the case of water-filled spherical shell,there are many fluid circumferential waves occurred due to internal fluid loading.The repulsion of phase velocity curve of adjacent fluid waves is obvious as a result of interaction between the internal fluid and elastic shells.

(3)The ability of the fluid wave re-radiation to the surrounding medium is reaching local extremum when the phase velocity of fluid wave for the water-filled shell is close to that of elastic waves for the evacuated shell.

[1]Nussenzveig H M.High-frequency scattering by an impenetrable sphere[J].Annals of Physics,1965,34:23-95.

[2]Nussenzveig H M.High-frequency scattering by a transparent sphere.I.Direct reflection and transmission[J].Journal of Mathematical Physics,1969,10:82-124.

[3]Nussenzveig H M.High-frequency scattering by a transparent sphere.II.Theory of the rainbow and the glory[J].Journal of Mathematical Physics,1969,10:125-176.

[4]Doolittle R D,Überall H,Uginius P.Sound scattering by elastic cylinders[J].J Acoust.Soc.Am.,1968,43(1):1-14.

[5]Rumerman M L.Increased accuracy in the application of the Sommerfeld-Watson transformation to acoustic scattering from cylindrical shells[J].J Acoust.Soc.Am.,1991,90(5):2739-2750.

[6]Rumerman M L.Application of the Sommerfeld-Watson transformation to scattering of acoustic waves obliquely incident upon cylindrical shells[J].J Acoust.Soc.Am.,1992,91(5):2502-2509.

[7]Gaunaurd G C.High-frequency acoustic scattering from submerged cylindrical shells coated with viscoelastic absorbing layers[J].J Acoust.Soc.Am.,1977,62(3):503-512.

[8]Williams K L,Marston P L.Backscattering from an elastic sphere:Sommerfeld-Watson transformation and experimental confirmation[J].J Acoust.Soc.Am.,1985,78(3):1093-1102.

[9]Paknys R,Jackson D R.The relation between creeping waves,leaky waves,and surface waves[J].IEEE Transactions on Antennas and Propagation,2005,53:898-907.

[10]Gaunaurd G C,Werby M F.Lamb and creeping waves around submerged spherical shells resonantly excited by sound scattering[J].J Acoust.Soc.Am.,1987,82(6):2021-2033.

[11]Gaunaurd G C,Werby M F.Sound scattering by resonantly excited,fluid-loaded,elastic spherical shells[J].J Acoust.Soc.Am.,1991,90(5):2536-2550.

[12]Überall H,Bjørnø I K,Bjørnø L.Dispersion of circumferential waves on evacuated,water-loaded spherical steel shells[J].Ultrasonics,2000,37:673-675.

[13]Sammelmann G S,Trivett D H,Hackman R H.The acoustic scattering by a submerged,spherical shell.I:The bifurcation of the dispersion curve for the spherical antisymmetric Lamb wave[J].J Acoust.Soc.Am.,1989,85(1):114-124.

[14]Sammelmann G S,Hackman R H.The acoustic scattering by a submerged,spherical shell.II:The high-frequency region and the thickness quasiresonance[J].J Acoust.Soc.Am.,1991,89(5):2096-2103.

[15]Hackman R H,Sammelmann G S.The acoustic scattering by a submerged,spherical shell.III:Pole trajectories in the complex-ka plane[J].J Acoust.Soc.Am.,1991,90(5):2705-2717.

[16]Tang Weilin.Relation between singularity expansion method(SEM)and resonance scattering theory(RST)[J].Acta Acustica.,1991,16(3):199-208.

[17]Pierce A D,Thurston R N.High frequency and pulse scattering[J].Physical Acoustics,San Diego,1992,21:Chapter 2.

[18]He Shipping.Research of wave propagation in viscoelastic tube and analysis of acoustic characteristics of anechoic coating[D].PhD thesis,Shanghai Jiao Tong University,2004.(in Chinese)

[19]Kodama M.Numerical calculation of the Bessel function of complex order using the recurrence method[J].IEICE TRANSACTIONS on Fundamentals of Electronics,Communications and Computer Sciences,1995,E78-A(4):506-516.

[20]Kodama M.New algorithm on the recurrence method for numerical calculation of Bessel function of complex order[J].IEICE TRANSACTIONS on Fundamentals of Electronics,Communications and Computer Sciences,1996,E79-A(4):621-623.

[21]Abdur R M,Kodama M.Numerical calculation of Bessel functions by solving differential equations and its application[J].IEICE TRANSACTIONS on Fundamentals of Electronics,Communications and Computer Sciences,1999,E82-A(10):2298-2301.

[22]Robert Paknys.Evaluation of Hankel functions with complex argument and complex order[J].IEEE Transactions on Antennas and Propagation,1992,40:569-578.

[23]Kodama M.A subroutine package for cylindrical functions of complex order and nonnegative argument[J].ACM Transactions on Mathematical Software,2008,34(4):1-21.