Steady Interaction Numerical Simulation of Cavitating Turbulent Flow between Ship Hull and Propeller

JU Lei,SU Yu-min,ZHAO Jin-xin,LIU Ye-bao,CUI Tong

(1 State Key Laboratory of Autonomous Underwater Vehicle,Harbin Engineering University,Harbin 150001,China;2 Shanghai Zhenhua Heavy Industry Co.,Ltd.,Shanghai 200125,China)

1 Introduction

Scholars at home and abroad have carried out a lot of research on cavitation performance of propeller,which have predicted and improved the cavitation performance of propeller.A test program was conducted to measure the alternating blade forces in inclined flow in a water tunnel where effects of cavitation could be assessed by Stuart Jessup et al[1].Shosaburo Yamasaki et al[2]discussed the effectiveness of cavitation control by tip load distribution as a propeller design parameter and presented the results of systematic experiments and numerical computations to develop practical design tools for high-performance marine propeller.A partial sheet cavitation model has been developed and implemented within a 3D BEM code to estimate the hydrodynamics forces and performance of a propeller working in an unsteady flow environment by Surasak Phoemsapthawee et al[3].Takashi Kanemaru et al[4-5]developed a calculation method for the steady and unsteady cavitating propeller problem based on a simple surface panel method‘SQCM’which satisfies the Kutta condition easily.Meanwhile,a calculation method for the pressure fluctuation on the hull surface induced by cavitating pro-peller has been proposed.Francesco Salvatore et al[6]summarized results from the Rome 2008 Workshop on cavitating propeller modelling and seven computational models by RANS,LES and BEM have been benchmarked against a common test case addressing the INSEAN E779A propeller in uniform flow and in a wakefield.

The cavitating flows around conventional and highly-skewed propellers in the behind-hull condition are simulated by an in-house RANS solver by Keun Woo Shin et al[7].The computed unsteady cavitation patterns in behind-hull condition and with respect to the blade angle have qualitatively acceptable accuracy,but with respect to the cavity extent,there are quantitative discrepancies.Experimental characterization of two CP propellers at different pitch settings,considering cavitating behaviour and related noise phenomena was conducted by Daniele Bertetta et al[8].FlorianVesting et al[9]presented an optimisation of a propeller blade with the propeller operating in behind conditions and considering sheet cavitation.Bart Schuiling et al[10]presented that the scale effect on the wake field of ship models was an important cause of prediction inaccuracies of hull pressure amplitudes at the first blade rate frequency,as induced by the cavitating propeller in model experiments.

Generally,when predicting cavitation performance of propeller,single propeller was considered and the interaction between the ship and the propeller was ignored.While in the prediction of wake field of ship without propeller,interference from propeller on the wake field was ignored.Based on these questions,calculation of ship and propeller as a whole has the certain superiority to improve the calculation precision of flow field.Interaction between the ship and the propeller was the key research topic in 20th International Towing Tank Conference.Wake field of ship is greatly affected by design of hull line and complexity of the disturbed wake field which has great influence on hydrodynamic performance of propeller.Abdel-Maksoud et al[11]adopted CFX-TASC flow to consider ship and propeller as a whole.Calculating program combining the flow field of ship and hydrodynamic performance of propeller has been applied to predict the disturbed flow field by Stern et al[12].Based on Computational Fluid Dynamics techniques and hybrid grid model,interaction between the ship and the propeller has been conducted by Zhang et al[13].Unsteady interaction hydrodynamic performance between the ship and the propeller has been predicted by Shen et al[14].The results demonstrated that propeller affected by wake field was mainly because the non uniformity of wake field changed the inlet velocity before propeller and the pressure distribution of blades.While propeller was a great influence on ship because the surface pressure distribution of ship was changed by the rotation and suction of propeller which gave rise to ship resistance.

2 Governing equation and cavitation model

The continuity and the momentum equations are as follows:

where uiand Fiare the velocity and body force in the i direction respectively,and P is the mixture pressure,and μ and μtare laminar viscosity and turbulent viscocity.

Conversion between water and vapor is described by cavitation model.A.K.Singhal Full Cavitation Model is applied in the paper.The working fluid is assumed to be a mixture of liquid,vapor and noncondensable gases.Standard governing equations in the mixture model and the mixture turbulence model describe the flow and account for the effects of turbulence.The cavitation model is as follows:

where f is vapor mass fraction,ρ is the mixture density,is the velocity vector of the vapor phase,γ is the effective exchange coefficient,and Reand Rcare the vapor generation and condensationrate terms.

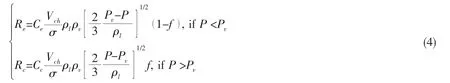
where Vchis a characteristic velocity,σ is the surface tension coefficient,and Pvis the saturation vapor pressure at 300K.Where Cεand Ccare empirical constants,0.02 and 0.01 respectively.

3 Geometry,meshing technique,and boundary conditions

A NACA66(MOD)airfoil section with camber ratio of 0.02,mean line of 0.8 and thickness ratio of 0.09 and DTRC4381 propeller were used to simulate steady cavitation flow.Computational domain and grid,and grid distribution are shown in Fig.1 and Fig.2.

Fig.1 Grid dividion of hydrofoil domain of NACA66

Fig.2 Mesh distribution of DTRC 4381 propeller

The mesh around the blades has been refined carefully to calculate the cavity evolution,especially the tip vortex cavitation.The boundary layer mesh was applied to ensure the nondimensional normal distance from the blade surface,and the first thickness and the number of the boundary layer are 0.000 1D and 7 with the ratio 1.1,respectively.Grid dividion of calculated domain of DTRC 4381 is shown in Fig.3.

Korea Research Institute of Ships and Ocean Engineering(KRISO)Container Ship(KCS)was selected as the object ship.Based on the information on geometrical shape and the experimental conditions of the KCS provided by KRISO,the ship model,named SRI M.S.No.631 was manufactured at the Ship Research Institute(SRI).The propeller model,named KP505,offered by KRISO,was selected as the object propeller.The principal particulars are given in Tab.1.The computational model of the interaction between the ship hull and the propeller are shown in Fig.4.

Fig.3 Grid dividion of calculated domain of DTRC 4381

Tab.1 Main parameters of KCS ship and KP505 propeller

Fig.4 Computational model of the interaction between the ship hull and the propeller

Prediction accuracy of the ship wake field determines validity of the interaction between the ship hull and the propeller.The quality and quantity of the grid affect the result of flow filed computation greatly.In the mesh distribution,there are with emphasis a few points:

(1)The size near the propeller disk and the bow is 0.003L,which has a gradual change to small-twisted part to control the mesh quantity,as shown in Fig.5.

(2)Six prism layers have been applied on the hull and propeller surface,and the first thickness is 0.003L with the ratio 1.1,as shown in Fig.6.

(3)Some important regions should be refined,that is,local refined region centers on the propeller disk and extends 4D to the bow,1D to the aft and 1.5D to the radial direction,respectively,as shown in Fig.7.

Fig.5 The mesh of ship surface

Fig.6 The prism layers of the ship and propeller

Fig.7 The local refined mesh near the propeller plane

The boundary conditions for the steady cavitation flow simulation are as follows:The undisturbed uniform velocity is given at the domain inlet,and the averaged static pressure is set at the domain outlet.The outer wall of the domain is regarded as the free slip wall while the solid surface of the propeller is set as the nonslip wall.SST k-ε turbulence model was selected.The governing equations were discretized using implicit method.The second order scheme was selected for the pressure,while the bounded central differencing scheme was selected for the momentum.For the velocity and pressure coupling,the SIMPLEC algorithm was used.

In all the simulations presented below,the working fluid is water at 300K,with liquid and vapor densities of 1 000 and 0.025 58 kg/m3,saturation pressure of 3 540 Pa and surface tension σ=0.071 7 N/m.

4 Numerical results

4.1 Steady cavitating flow over a hydrofoil

To study the effect of different cavitation number on hydrofoil,the cavitation numbers of 0.84,0.91 and 1.0 with the chord length of 0.1 m and the attack angle of 4°were chosen to get the pressure variation[15]and the total volume fraction distributions on the suction side of the hydrofoil,shown in Fig.8.From comparison with the experimental data,pressure distribution on the suction side of the hydrofoil was predicted satisfactorily in a wide range of cavitation number by using the present method.

It can be seen from Fig.8 that the pressure coefficients of suction side with three different cavitation numbers were predicted satisfactorily compared with the experimental data.The coverage area of cavitation is related to cavitation number.When V∞was kept constant,cavi-tation number was varied by changing P∞,and the larger the cavitation number,the smaller the coverage area of cavitation.

Fig.8 The pressure coefficient of suction side and volume fraction distribution with different cavitation number

Fig.9 Calculational and experimental results of steady cavitation of DTRC 4381

4.2 Cavitation performance of propeller

The cavitation number of 3.5 and the advance ratio of 0.7 were chosen in this part.The calculational and experimental data[16]are shown in Fig.9.

4.3 Prediction of wake field

Tab.2 represents the computational and experimental results of resistance coefficient of the ship.From the table,it can be seen that the error reaches-2.1%.

Tab.2 Resistance coefficient of KCS ship without propeller

The computational and experimental results obtained by Fujisawa et al[17]of the ship pressure coefficient without propeller are shown in Fig.10.However,there is some distortion near the waterline.The reason is because the wave of free surface was not concerned.

Fig.10 Calculation and experimental results of surface pressure distribution on ship hull without propeller

The computational and experimental results[18]of the wake field are shown in Fig.11.Comparison with the experimental data,the axial,tangential and radial components are basically accurate.

Fig.11 Calculation and experimental results of local velocity field at 0.25D behind the propeller plane of ship without propeller

4.4 Steady cavitation interaction between the ship and the propeller

The undisturbed uniform velocity,i.e.,V=2.196 m/s,is given at the domain inlet,and the averaged static pressure is set at the domain outlet.Multiple Reference Frame model is selected for propeller rotation.The wall Y plus of KP505 propeller and KCS ship is shown in Fig.12.

Cavitation number is one of the most important parameters in the simulation of cavitating turbulent flow.Surface pressure distribution on propeller changes versus cavitation number.To study the effect of different cavitation number on propeller,the cavitation numbers of 3.0,3.5 and 3.75 were chosen to get the pressure variation and the gas volume fraction distribution on the propeller,shown in Fig.13.It is also clarified that the smaller the cavitation number,the larger the coverage area.

Fig.12 Wall Y plus of KP505 propeller and KCS ship

Fig.13 Contours of static pressure and vapor fraction with different cavitation number

5 Conclusions

Based on the present study,the following conclusions can be drawn:

(1)The numerical method to predict cavitation performance of propeller is usable to simulate the interaction between the ship and the propeller.

(2)The results obtained from the steady cavitation simulation of airfoil and propeller show that the pressure coefficient and vapor coverage areas are predicted satisfactorily compared with experimental measurement.

(3)It is clarified that ship and propeller could be considered as a whole when computing steady cavitation interaction between the ship and the propeller.For cavitation performance optimization of existing ship now,adding appendages before propeller has some feasibility in practice to improve the flow field before propeller.

[1]Stuart Jessup,Martin Donnelly,Ian McClintock,Scott Carpenter.Measurements of controllable pitch propeller blade loads under cavitating conditions[C]//First International Symposium on Marine Propulsors.Trondheim,Norway,2009.

[2]Shosaburo Yamasaki,Akinori Okazaki,Nobuhiro Hasuike,Yasutaka Kawanami,Yoshitaka Ukon.Numerical and experimental investigation into cavitation of propellers having blades designed by various load distributions near the blade tips[C]//First International Symposium on Marine Propulsors.Trondheim,Norway,2009.

[3]Surasak Phoemsapthawee,Jean-Baptiste Leroux,Jean-Marc Laurens,François Deniset.A versatile partial sheet cavitation model[C]//First International Symposium on Marine Propulsors.Trondheim,Norway,2009.

[4]Takashi Kanemaru,Jun Ando.Numerical analysis of steady and unsteady sheet cavitation on a marine propeller using a simple surface panel method“SQCM”[C]//First International Symposium on Marine Propulsors.Trondheim,Norway,2009.

[5]Takashi Kanemaru,Jun Ando.Numerical analysis of pressure fluctuation on ship stern induced by cavitating propeller using a simple surface panel method“SQCM”[C]//Second International Symposium on Marine Propulsors.Hamburg,Germany,2011.

[6]Francesco Salvatore,Heinrich Streckwall,Tom van Terwisga.Propeller cavitation modelling by CFD-Results from the VIRTUE 2008 Rome Workshop[C]//First International Symposium on Marine Propulsors.Trondheim,Norway,2009.

[7]Keun Woo Shin,Poul Andersen,Robert Mikkelsen.Cavitation simulation on conventional and highly-skewed propellers in the behind-hull condition[C]//Second International Symposium on Marine Propulsors.Hamburg,Germany,2011.

[8]Daniele Bertetta,Luca Savio,Michele Viviani.Experimental characterization of two CP propellers at different pitch settings,considering cavitating behaviour and related noise phenomena[C]//Second International Symposium on Marine Propulsors.Hamburg,Germany,2011.

[9]FlorianVesting,Rickard Bensow.Propeller optimisation considering sheet cavitation and hull interaction[C]//Second International Symposium on Marine Propulsors.Hamburg,Germany,2011.

[10]Bart Schuiling,Frans Hendrik Lafeber,Auke van der Ploeg,Erik van Wijngaarden.The influence of the wake scale effect on the prediction of hull pressures due to cavitating propellers[C]//Second International Symposium on Marine Propulsors.Hamburg,Germany,2011.

[11]Paik B G,Kim.Analysis of wake behind a rotating propeller using PIV technique in a cavitation tunnel[J].Journal of O-cean Engineering,2007,34(3-4):594-604.

[12]Stern F,Kim.A viscous flow approach to the computation of propeller-hull interaction[J].Journal of Ship Research,1988,32:246-262.

[13]Zhang Zhirong,Li Baiqi,Zhao Feng.Integral calculation of viscous flow around ship hull with propeller[J].Journal of Ship Mechanics,2004,8(5):19-26.

[14]Shen Hailong.Research on the unsteady interaction between ship hull and energy-saving appendage and propeller[D].Harbin:Harbin Engineering University,Ph.D.Thesis,2010.

[15]Shen Y T,Dimotakis P.The influence of surface cavitation on hydrodynamic forces[C].Proceedings of 22nd American Towing Tank Conference,St Johns N F,1989:44-53.

[16]Jules W Lindau,David A Boger,Richard B Medvitz,Robert F Kunz.Propeller cavitation breakdown analysis[J].Journal of Fluids Engineering,2005,127:995-1002.

[17]Fujisawa J,et al.Surface pressure measurements on the KCS Model(SRI M.S No.631)in the SRI 400 m towing tank[R].SPD Report No.00-004-01.Ship Performance Division,Ship Research Institute,2000.

[18]Fujisawa J,et al.Local velocity field measurements around the KCS Model(SRI M.S No.631)in the SRI 400 m towing tank[R].SPD Report No.00-003-02.Ship Performance Division,Ship Research Institute,2000.