Dynamic Optimization of Ship Grillages based on Grillage Dynamic Stiffness Algorithm and Scheme Database

HE Li,CHENG Yuan-sheng,LIU Jun

(School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)

1 Introduction

Grillage systems are widely used in bridge decks,ship hulls and offshore platforms.With their vibration reduced,the structural safety margin can be improved,as well as the working performance of the equipment installed on them.In the previous researches about the structural optimization for grillage systems,the most considered the optimization of the grillages under static loads[1-3].A genetic algorithm based method was developed for the optimum design of grillage systems which found the optimum number of required beam and selected the optimum section from a set of standard universal beam sections[1].A harmony search algorithm was utilized to investigate the effect of the spacing between the longitudinal and transverse beams of a grillage system[2].The genetic algorithms were also used to optimize the FRP composite grillages in ship structures and to obtain discrete optimal results[3].

The structural optimization for vibration reduction was concerned by some researchers[4-7].The vibration of a spring-supported beam with a controller was suppressed by iteratively executing structural optimization and controller optimization[4].Both serial and parallel approaches to combine structural optimization and controller optimization were investigated.Later,sensitivity analyses of eigensolutions and eigenfunctions of 3-D frame structures was derived using Timoshenko beam theory[5].Based on the sensitivity data,the minimum weight design with an exact frequency constraint could be carried out efficiently.An integrated control-structural design optimization method,which was based on the design sensitivity analysis for structural dynamics in time domain,was proposed to the vibration control of piezoelectric intelligent truss structure[6].Recently,based on adaptive evolutionary strategies,a dynamic optimization method for stiffened plate was proposed[7].This method could reduce the structural vibration and improve the comfort and the safety of the vessel.Besides,some researchers presented an equivalent static load method,which is based on the transformation of dynamic loads to static loads through the structural displacement vector and stiffness matrix[8-9]and can be applied to structural shape optimization considering the dynamic stress constraints efficiently.These papers provided useful algorithms for the optimization of vibration structures,but the optimization for grillage system with some vibration isolators has seldom been considered.

The dynamic stiffness method is a useful tool for structural dynamic analysis.Many researchers used this method to simplify structural dynamic model and to improve calculation efficiency.The dynamic stiffness method was used for the dynamic stiffness formulation of a Bernoulli-Euler beam carrying a spring-mass system[10].And an exact dynamic stiffness method was developed for predicting the free vibration characteristics of a three-beam system[11].However,application of the dynamic stiffness method for structural dynamic analysis of grillage systems was rather limited.

As an extension of the dynamic stiffness method,the grillage dynamic stiffness(GDS)algorithm is presented to analyze dynamic response of grillage systems in the paper.A grillage system is divided into discrete beams and the dynamic equations of these discrete beams are obtained using the dynamic stiffness method.Afterwards the global dynamic equation of the grillage system is generated by assembling the dynamic equations of these beams and is solved accordingly.Then the natural frequency and dynamic response of the grillage system with and without isolators can be calculated very quickly by using GDS algorithm contrasted with the traditional FEM method.Furthermore,the equivalent static load method together with the GDS algorithm is employed to obtain the dynamic stress distribution conveniently.For the little computational cost of the GDS algorithm,the vibration performance of a grillage system with different vibration isolators could be mathematically optimized considering the constraints of the total weight and dynamic stress of the structure.Furthermore,the discrete optimal design of beams can be obtained by using proposed scheme database strategies combining with the GDS algorithm.

2 Grillage dynamic stiffness algorithm

2.1 Dynamic stiffness method applied to the grillage system

A ship grillage system which consists of longitudinally and transversely beams is often subjected to vertical dynamic loads.The vertical bending of beams of the system is the main structural deformation form and the effect of the beam’s axial torsion is usually very small.In the analysis,the axial torsion of the beams could be neglected and their vertical bending is considered only.A grillage system under dynamic loads is divided into discrete beams as illustrated in Fig.1.Assume that the external loads are applied on the transversal beams along y-axis and the longitudinal beams along x-axis only endure the internal loads.

Fig.1 The discretization of a grillage system

In the study,the dynamic stiffness method is used to obtain the dynamic equations of each beam without considering their axial torsion.For beams i and j as example,the dynamic displacement of the intersection point（i,j）of the two beams can be expressed as:

where both xijand xjiare the dynamic displacement of the intersection point of beams i and j.the dynamic flexibility of point（i,j）to point（i,k）of the transversal beam i,Qjikthe dynamic flexibility of point（i,j）to point（k,j）of the longitudinal beam j,fi1,…,finand n1j,…,nmjthe external and internal loads on the intersection points of the transversal beam i and the longitudinal beam j respectively,fit1,…,fitsthe external loads on the other points of the transversal beam i.

For the intersection point of beams i and j,it exists

And the Eq.(1)and Eq.(2)can be merged as

Likewise the dynamic equations of other points can also be obtained and the dynamic displacement of the grillage system could be calculated conveniently by simultaneously solving these equations.

2.2 Dynamic flexibility of a beam under concentrated load

In the study,Lagrange equation and mode superposition method are used to obtain the dynamic flexibility of a Bernoulli-Euler beam under dynamic concentrated load as shown in Fig.2.According the Ref.[12],the transverse displacement of a vibration beam can be expressed as a linear combination of mode shape function and characteristic function

Fig.2 A beam under concentrated load

where ηr（t）is the r order characteristic function and Yr（x）the r order mode shape function.

The kinetic energy and potential energy of beam’s bending vibration are respectively expressed as:

when the external load is harmonic load,the expression of the load’s virtual work can be written as

Substitute Eq.(6),Eq.(7)and Eq.(8)into the Lagrange equation as expressed by Eq.(9),one may get the kinetic equation as represented by Eq.(10),

where ωris the r order natural circular frequency of the beam.

Solving Eq.(10),the transverse displacement of the beam is given by

Then the dynamic flexibility of point j to point i can be expressed as

For the beam with different boundary conditions,the dynamic flexibility could be easily obtained using the corresponding expressions of its natural frequency and mode shape function.

2.3 Vibration isolation analysis of a grillage system

Many machines are usually installed on ship grillage systems with different vibration isolators.Using the GDS algorithm,the structural vibration of these systems can be analyzed easily.As illustrated in Fig.3,a machine is installed on the grillage system with a single-stage vibration isolator.In vibration analysis,the machine can be treated as lumped mass under harmonic load.Using the four pole parameter method[12],the structural vibration equations of the isolation system can be expressed as

Fig.3 A grillage system with a single-stage vibration isolator

where fijis the load on point（i,j）and xijthe dynamic displacement of point（i,j）.And using the GDS algorithm in section 2.1,the dynamic stiffness equation of the grillage system can be easily expressed as

where C is the dynamic stiffness matrix composed of the dynamic flexibilities of the longitudinal and transversal beams;

Fig.4 A grillage system with a two-stage vibration isolator

Then the structural vibration solution can be obtained by solving the simultaneous equations of Eq.(13)and Eq.(14).

When a machine with a two-stage vibration isolator is installed on a ship grillage sys-tem as illustrated in Fig.4,the vibration equations of the machine system become:

where ftis the load on the lumped mass m2and xtthe dynamic displacement of the lumped mass m2.Then the structural vibration solution could be obtained by solving the simultaneous equations of Eqs.(14)-(16).

Fig.5 A grillage system with a pedestal

As shown in Fig.5,a machine is installed on the middle of a pedestal and the pedestal is connected to the points（i,j）and（i,j+1）with two single-stage vibration isolators.In order to simplify the vibration analysis,the machine is treated as a lumped mass and the pedestal is taken as a rigid body without weight.The vibration equations of the machine system become

wherefm1andfm2are the loads on the two single-stage vibration isolators;fijandthe load on points（i,j）and（i,j+1）respectively;xijandthe dynamic displacements of pointsandrespectively.

Similarly,the structural vibration solution of the grillage system with machine installed could be computed by solving the simultaneous equations of Eqs.(14),(17)-(19).It should be noticed that the expression of F in Eq.(14)now becomesinstead.The structural vibration isolation indexes such as power flow and force transmissibility can be further obtained conveniently.

2.4 Structural dynamic stress distribution calculation

In order to consider the stress constraints in vibration optimization,the GDS algorithm is combined with the equivalent static load method to produce the structural dynamic stress distribution.The equivalent static load method[8-9]is based on the transformation of dynamic loads to static loads through the structural displacement vector and stiffness matrix.The main procedures of the equivalent static load method are summarized as follows.

Using the vibration theory with the finite element method(FEM),the dynamic behavior of a structure is expressed by the following differential equation

where M,C and K are the mass matrix,damping matrix and stiffness matrix,respectively,F the vector of external dynamic loads,and d the vector of dynamic displacement.The static analysis FEM formulation is expressed as

where dstaticis the vector of static displacements and Fstaticthe vector of external static loads.Therefore,the equivalent static load Feq,which can generates the same displacement field as that from dynamic loads at an arbitrary time ta,is expressed as

After the transformation,the equivalent static load can be used to replace the dynamic load in structural dynamic analysis to make the same displacement field and the same stress field.

In this paper,the dynamic displacement computed by the GDS algorithm is transformed to equivalent static load,which is expressed as

where dGDSis the dynamic displacement computed by the GDS algorithm.And using the equivalent static load,the structural stress distribution can be easily calculated in structural static analysis.

2.5 Results comparison between GDS algorithm and FEM method

As Fig.6 illustrated,a ship grillage is treated as a combination of intersection beams.The cross-sections of longitudinal girders along x-axis and transverse beams along y-axis are divided into four groups.The modulus of material elasticity is 200 GPa and the material density is 7 900 kg/m3.There are two pillars with cross-section area of 18 cm2and height of 2.1 m connected with points A and C of the grillage.The thickness of the deck is 4 mm and the dimensions of the longitudinal girders and transverse beams are given in Tab.1.

Fig.6 A ship deck grillage

Tab.1 Dimensions of the girders and beams(mm)

Using the GDS algorithm coded in MATLAB[13],the structural dynamic stiffness equation CX=F can be easily obtained.Solving the equation（C）=0,the natural frequencies of the grillage system’s vertical vibration can be obtained.Tab.2 lists the first five mode natural frequencies.It is seen that the results obtained from GDS algorithm agree well with ones from the traditional FEM method carried out in ANSYS[14].The max deviation is only 2.69%and the calculating time of the GDS algorithm is less than one second,which is much less than one of FEM method.

Tab.2 Natural frequencies computed by different methods

And then a machine with a single-stage vibration isolator installed on the point B of the ship grillage as shown in Fig.6 is further taken into account.The machine endures a harmonic load with amplitude of 15 kN.The mass of the machine is 600 kg.The elastic coefficient and damping coefficient of the isolator are 1 200 kN/m and 8 000 Ns/m,respectively.As Figs.7-8 shown,the dynamic displacement amplitudes of the machine and force transmissibility of the isolator calculated by the GDS algorithm and FEM method show good agreement when the load’s frequency varies from 1 Hz to 40 Hz.The calculation time of the GDS algorithm is no more than one second,which is only about five percent of the FEM method.

Fig.7 Spectrum curve of displacement amplitude of the machine

Fig.8 Spectrum curve of force transmissibility of the isolator

3 Dynamic optimization method of ship grillages

In the study,the dynamic optimization of a ship grillage is to select both the dimensions of longitudinal and transverse beams and the parameters of the isolators and to minimize either the power flow transmitted to the basic grillage system or the force transmissibility of vibration isolator or the velocity amplitude of the machine under the constraints of total weight of the grillage and dynamic stress.The mathematical model of the dynamic optimization of a ship grillage system is expressed as follows:

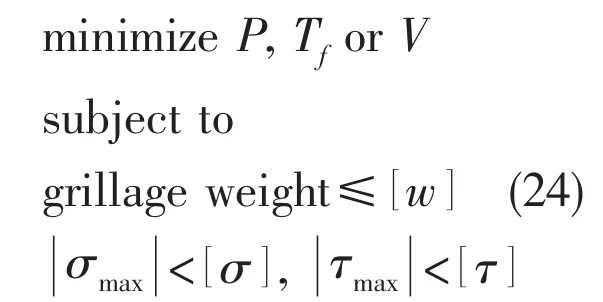
where P is the power flow transmitted to the basic grillage system,Tfthe force transmissibility of vibration isolator,and V the velocity amplitude of the machine.

In the analysis,the above mentioned GDS algorithm and the equivalent static load method are employed to compute the dynamic response and dynamic stresses of the grillage structures due to their high computational efficiency.To reduce the number of design variables,the inertia moment of the beams are selected to be the design variables and a scheme database strategy is proposed to obtain discrete dimensions of beams which may be used in engineering directly.

Fig.9 depicts the principle of scheme database strategy.The scheme database is a database which consists of all possible T-shape beam design schemes satisfying section design requirements.When a given value of inertia moment of a beam that is determined by an optimization algorithm such as the sequential quadratic programming(SQP)algorithm used in the analysis is available,a detailed design scheme for the beam with the smallest cross section area and inertia moment being larger than required one can be selected from the scheme database.By using the strategy,the required dimensions of beams for dynamic analysis are available and the decrease in the number of design variables is carried out and finally the discrete optimal dimensions of beams are obtained as well.

Fig.9 Principle of scheme database strategy

4 Numerical examples

As Fig.6 illustrated,the basic ship grillage system is the same as the one in section 2.5 and different vibration isolators are installed on it.The cross-sections of longitudinal girders and transverse beams are also divided into four groups.The influence of longitudinals on structural vibration is not considered in optimization.The complex elasticity modulus of the structure is 200×（1+0.1j）GPa and the material density is 7 900 kg/m3and the structure endures uniform hydrostatic pressure with value of 5 kPa.The mass of the machine is 600 kg.The frequency and amplitude of the harmonic load on machine is 24 Hz and 30 kN.Three cases are considered.Case 1 is to minimize the power flow transmitted to the basic grillage system and case 2 the velocity amplitude of the machine and case 3 the force transmissibility of the isolator,respectively.The max normal stress,max shear stress,first order natural frequency,critical stress of longitudinal buckling and time cost of optimization are all given in numerical examples.In optimization the following constraints are considered:

4.1 A machine with a single-stage vibration isolator

A machine with a single-stage vibration isolator as shown in Fig.10 is installed on the point B of the basic grillage system as shown in Fig.6.The optimal results for three cases un-der consideration are given in Tabs.3-4.For the purpose of comparison,the initial values of structures are also included in Tabs.3-4.As Tab.3 shown,the dynamic performance of the optimal grillage system is much improved than the one of the initial design.The optimal dimensions of structures change depending on the objective function to be minimized,but the optimal elastic coefficient of the isolator keeps unchanged for three cases.And when the velocity amplitude of the machine becomes optimal objective,the power flow transmitted to the basic grillage system of the optimal design is slightly increased than the one of initial design.It may be the reason that appropriate enhancement of the vibration of the basic grillage system is helpful to dissipate more vibration energy and to reduce the vibration of the machine.Besides,the value of the structural max shear stress is very small contrasted with the one of the structural max normal stress.It is because the structural stress is mainly caused by the uniform hydrostatic pressure and the value of the normal stress of structures which endures uniform loads would be much larger than the one of the shear stress according to corresponding mechanical principle.

Fig.10 Single-stage vibration isolator

Tab.3 Initial values and the optimum results of the grillage with a single-stage vibration isolator

Tab.4 The optimal design schemes of the girders and beams(mm)

Continue

4.2 A machine with a two-stage vibration isolator

Similar to the section 4.1,as Fig.11 illustrated,a machine with a two-stage vibration isolator has been installed on the point B of the basic grillage system.The optimal results for three cases under consideration are given in Tabs.5-6.As Tab.5 shown,the structural vibration is less than the grillage system with a single-stage vibration isolator in section 4.1 for the intermediate mass of the isolator is helpful to dissipate a lot of vibration energy and to reduce structure vibration.Properly reducing the elastic coefficient and increasing the intermediate mass of the two-stage isolator are useful to decrease the power flow transmitted to the basic grillage system and force transmissibility of the isolator.But this rule would not keep effective if the optimal objective is the velocity amplitude of the machine.When the velocity amplitude of the machine becomes optimization objective,the weight of the intermediate mass of the two-stage isolator has been decreased along with the increase of the weight of the basic grillage system.And it could be also seen that optimization for the velocity amplitude of the machine would lead to slightly increase of the power flow transmitted to the basic grillage system and force transmissibility of the isolator compared with the initial design.

Fig.11 Two-stage vibration isolator

Tab.5 Initial values and the optimum results of the grillage with a two-stage vibration isolator

Continue

Tab.6 The optimal design schemes of the girders and beams(mm)

4.3 A machine with a pedestal

As Fig.12 shown,a machine is installed on the middle of a pedestal and the pedestal with two single-stage vibration isolators is connected to the points B and C of the basic grillage system as shown in Fig.6.Because the dynamic flexibilities of point B and point C of the ba-sic grillage system are different,the machine may not keep horizontal vibration under external dynamic load.When the velocity amplitude of the machine becomes optimal objective,it should be satisfied that the pedestal keeps horizontal vibration under external load.

The optimal results for three cases under consideration are given in Tabs.7-8.As Tab.7 shown,the structural vibration is stronger than the grillage system with a two-stage vibration isolator in section 4.2 and the optimal elastic coefficient of the two isolators keeps unchanged for three cases.Besides,the optimal velocity amplitude of the machine is a little larger than the ones in sections 4.1 and 4.2.It may be the reason that the optimization efficiency has been affected by the additional constraint.

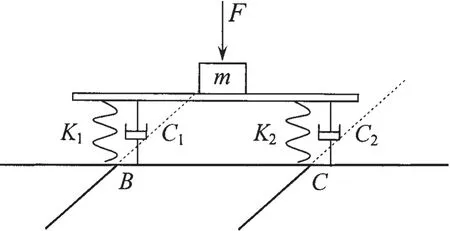
Fig.12 Pedestal with two single-stage vibration isolators

Tab.7 Initial values and the optimum results of the grillage with a pedestal

Tab.8 The optimal design schemes of the girders and beams(mm)

Continue

5 Conclusions

A novel structural dynamic optimization method,which is based on the grillage dynamic stiffness algorithm and discrete scheme database,is presented in this paper.Using this method,the vibration performance of ship grillage system with different isolators could be optimized and discrete structural parameters can be obtained considering the constraints of structural stress and total weight of the system.Some optimization examples are presented and excellent solutions are obtained.It is shown that the proposed method is efficient and reliable.

The optimization examples indicate that the vibration performance of ship grillage system could be improved obviously by proper selecting the structural parameters without increasing the mass of the structure.And the structural parameters would alter along with the change of the optimal objective.It should be noted that the vibration of the basic grillage system would be increased when the vibration performance of the machine becomes the main factor considered in optimization.

[1]Saka M P,Daloglu A,Malhas F.Optimum spacing design of grillage systems using a genetic algorithm[J].Advances in Engineering Software,2000,31(11):863-873.

[2]Erdal F,Saka M P.Effect of beam spacing in the harmony search based optimum design of grillages[J].Asian Journal of Civil Engineering(Building and Housing),2008,9(3):215-228.

[3]Maneepan K,Shenoi R A,Blake J I R,Jeong H K.Genetic algorithms(GAs)based optimization of FRP composite plated grillages in ship structures[J].Transactions of the Royal Institution of Naval Architects Part A:International Journal of Maritime Engineering,2007,149(3):1-19.

[4]Zhu Y,Qiu J H,Tani J,Urushiyama Y,Hontani Y.Simultaneous optimization of structure and control for vibration suppression[J].Journal of Vibration and Acoustics,1999,121(2):237-243.

[5]Yu J F,Wang B P.An optimization of frame structures with exact dynamic constraints based on Timoshenko beam theory[J].Journal of Vibration and Acoustics,2004,269(3-5):589-607.

[6]Zhao G,Chen B,Gu Y.Control-structural design optimization for vibration of piezoelectric intelligent truss structures[J].Structural and Multidisciplinary Optimization,2009,37(5):509-519.

[7]Wang H H,Hong M,Chen F,An X T.Dynamic optimization of stiffened plate based on adaptive evolutionary strategies[J].Shipbuilding of China,2011,52(2):130-138.

[8]Choi W S,Park G J.Structural optimization using equivalent static loads at all time intervals[J].Computer Methods in Applied Mechanics and Engineering,2002,191(19-20):2077-2094.

[9]Park K J,Lee J N,Park G J.Structural shape optimization using equivalent static loads transformed from dynamic loads[J].International Journal for Numerical Methods in Engineering,2005,63(4):589-602.

[10]Banerjee J R.Dynamic stiffness formulation and its application for a combined beam and a two degree-of-freedom system[J].Journal of Vibration and Acoustics,2003,125(3):351-358.

[11]Jun L,Hongxing H.Dynamic stiffness vibration analysis of an elastically connected three-beam system[J].Applied A-coustics,2008,69(7):591-600.

[12]Harris C M,Crede C E.Shock and Vibration Handbook[M].New York:McGraw-Hill,1976.

[13]Mathworks.Matlab User’s Guide[K].Natick,MA,1993.

[14]ANSYS.Engineering analysis system user’s manual[K].Swanson Analysis Systems,Inc.,1989.