饱和软土地基沉降计算方法

李百明 （天津凯德投资有限公司 天津300308）

刘永光 （天津城投集团 天津300202）

饱和软土地基沉降计算方法

李百明 （天津凯德投资有限公司 天津300308）

刘永光 （天津城投集团 天津300202）

软土是一种区域性的特殊土，是在一定的地质条件下形成的，具有变形大、承载力低等特点。软土地基具有高含水量、高压缩性、低强度、低渗透性和高灵敏度的特点，其地基稳定性差，不易满足建筑物地基设计要求，直接影响结构工程的稳定性和耐久性，一般都需进行处理才能满足工程设计要求。简要介绍了软土的特点和工程特性，论述了饱和软土地基沉降计算中需要考虑的土体的自重应力计算、基底附加压力随地基沉降变化的影响、加载方式和加载速率的影响等关键问题，分别给出了瞬时沉降、固结沉降和次固结沉降3个阶段的饱和软土地基沉降量计算方法。

软土 地基沉降 瞬时沉降 固结沉降 次固结沉降

0 引言

软土是一种区域性的特殊土，是在一定的地质条件下形成的，具有变形大、承载力低等特点。在软土地区的工程建设需要特别重视了解和研究软土的工程特性，采取有针对性的技术措施以使建设工程得到技术先进、经济合理和使用安全的效益。

软土的工程性质取决于软土的成因和成分，也取决于地层的构造，即软土的厚度、埋藏深度及其与上覆或下卧的比较坚硬土层的相对位置，因此在研究软土的工程性质时，必须注意其成因类型及构造。我国软土的分布，按区域性可分为沿海软土、内陆软土和山区软土。不同成因的软土，其物质组成、物理性质和力学性质都有一定的差别。

软土通常是指由天然含水量大、压缩性高、承载能力低的淤泥沉积物及少量腐殖质组成的土，主要有淤泥、淤泥质土及泥炭。具有高含水量、低强度、高压缩性、低透水性和中等灵敏度的特点，一般含水量高达45%～50%，大于液限，孔隙比大于1.0，塑性指数为20左右，强度为10～30 kPa，压缩系数为0.5～1.0 MPa-1，固结系数为（0.1～1.0）×10-3cm2/s，灵敏度为4～8。[1]因此，软土地基具有高含水量、高压缩性、低强度、低渗透性和高灵敏度的特点，其地基稳定性差，不易满足建筑物地基设计要求，直接影响结构工程的稳定性和耐久性，一般都需进行处理才能满足工程设计要求。

当前，随着我国沿海及湖区等软土地区铁路和高速公路的发展，软土地基的沉降问题日益突出。因此，深入探讨软土地基的沉降发展机理，研究长期循环荷载作用下软粘土的强度和变形特性，进而采取合适的防治措施，并将它应用于实际工程中，不但具有很高的学术价值，而且也具有广泛的工程实际意义。

1 饱和软土地基沉降计算中的问题

土是一种由颗粒（固相）、水（液相）、气（气相）所组成的三相体系，最主要的特征是它的碎散性和自然变异性。这是它的变形、强度等力学性质上都与连续固体介质有根本不同的内在原因。影响地基沉降计算的问题不少，其中主要有以下几点：

1.1 土体自重应力的计算

软土地基中的地下水位通常很高，对于地下水位以下的土体，当其液性指数为0＜It＜1时，土颗粒是否受到水的浮力作用，浮力多大，尚无法确定，从而影响到此种情况下的土中应力计算，目前只能按对工程不利的情况考虑。在地基沉降计算中采用浮容重计算自重应力，这对沉降计算结果必然会产生较显著的影响。[2]

1.2 基底附加压力随地基沉降变化的影响

当软土地基上的荷载是填土时，一方面，在施工期间的地基沉降由后继填土补填起来，从而使实际填土荷载大于原设计荷载；另一方面，当地下水位很高时，沉至地下水位以下的填土会受到浮力作用，导致基底附加压力减小。对于前一因素，目前还缺少理论分析方法，工程中通常对地基沉降较大的情况作适当的经验修正，即工程中所谓的超填修正问题。对于后一因素，Baligh[3]、朱向荣等人[4]曾针对地基一维沉降情况，提出了土中应力随地基沉降减小的计算方法。朱向荣等人的计算表明，土中应力的减小对软土地基沉降计算的影响是相当显著的。事实上，由地基沉降导致的超填荷载与填土浸水后受到的浮力作用，对沉降量的影响具有互补性，故在沉降分析中应对这两方面的影响综合考虑，否则将会导致更大的误差。

1.3 土体应力历史的影响

工程实践表明，软土地基通常由多种土层组成，其中一些土层可能处于超固结或欠固结状态。如我国沿海地区的软土层上常有1.0～3.0 m的超固结硬壳层，而近海地区的软土层往往处于欠固结状态。土体的应力历史不仅对地基沉降量产生影响，也影响土体的固结特性。如欠固结土，由于先期固结应力小于现在的自重应力，即在自重应力作用下尚未完全固结，当在地基上没有外荷载时，土中有效应力也在增加，直到有效应力增大到自重应力，只要外荷载引起的附加应力与自重应力之和小于或等于自重应力，土体的变形就必定很小，故可近似认为不产生排水固结变形。Ohara[5]和Dudd[6]研究了沉降-时间曲线对各种非线性关系曲线的敏感程度，结果表明，超固结粘土大大地延缓了沉降过程。粘性土中初始水力梯度的存在，也是对沉降-时间关系曲线产生影响的重要因素。超固结土的初始水力梯度一般较大，土中水的渗流只有克服了土粒间结合水的堵塞才可能产生。当外荷载较小时，土中超静水压力不可能完全消散。

目前，对于一维最终沉降的计算已有了考虑应力历史影响的理论方法。在地基沉降-时间关系的分析方面，现有的理论计算方法都未能考虑应力历史的影响。

1.4 加载方式和加载速率的影响

实际施工中的加载方式变化很大，采用不同的加载方式和加载速率，地基的沉降-时间曲线显著不同。Terzaghi（1925年）[7]曾根据施工荷载直线增大的规律给出了地基一维固结沉降的计算方法及图解曲线。但该方法属于线弹性理论。若采用非线性变形理论，考虑施工加载对沉降-时间曲线的影响，则还需要进一步探讨。

2 考虑不同变形阶段的饱和软土地基总沉降量计算方法

在外荷载作用下，地基土体发生变形，地面产生沉降。按地基在荷载作用下发生变形的过程，可以认为地基最终沉降量S是由3个部分组成，即：瞬时沉降Sd、固结沉降Sc和次固结沉降Ss，用公式表示为：

2.1 瞬时沉降计算

初始沉降即瞬时沉降，是地基土在不排水加载期间产生的，是剪应变引起的。对于严格的土体一维变形情况，瞬时沉降很小。当土体完全饱和时，由于土中水及土颗粒本身的变形可忽略不计，故瞬时沉降很小。当软粘土地基的厚度深、上部荷载大、加荷速率高时，瞬时沉降在总沉降中占相当大的比例。瞬时沉降包括两部分：一部分是由于地基的弹性变形产生的；另一部分则由于地基塑性区的开展，继而扩大所产生的侧向剪切位移。对于前一部分，一般用弹性理论公式来计算，后一部分至今仍无令人信服的计算方法，多在前一部分计算结果的基础上进行修正。瞬时沉降的理论计算方法主要有如下几种：

2.1.1 对于作用于地面上的圆形或矩形面积均布荷载，瞬时沉降可按下述弹性理论法（解析法）来估计，即：

式中：Fd为考虑荷载面积形状和沉降计算点位置的系数；p为均布荷载，kPa；B为荷载面积的直径或宽度，m；E和μ分别为图的弹性模量（kPa）和泊松比。

2.1.2 对于路堤、防波堤等荷载，地基受力模式为半无限长条形的分布荷载形。（2）式变为：

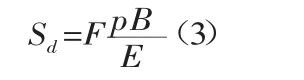
式中：F为沉陷系数，可由相关图查得；p为堤基面中心线上的梯形荷载强度，kPa；B为换算荷载宽度，；E为地基土的弹性模量，kPa。

饱和粘土在开始加荷时，认为体积是不可压缩的，因此令泊松比μ=0.5。弹性理论法是将地基视为半无限空间弹性体，通过弹性理论求解地基在荷载作用下的变形。采用该法计算的困难之处在于确定弹性系数。而且土体并不是弹性体，采用弹性理论法较难得到合理解答。

2.2 主固结沉降的计算

主固结沉降是因为地基土在荷载作用下将产生超静孔隙水应力，随着时间的推移，超静孔隙水应力将逐步消散，地基土孔隙中的水排出，地基土体积减小，地表产生沉降。主固结沉降是地表沉降的主要组成部分，从一次性加载算起，任意时刻的主固结沉降为：

式中：Sc为地基的最终沉降量；Ut为地基的平均固结度。上式表明，地基主固结沉降的计算包括两个部分，即地基固结度的计算和地基最终沉降量的计算。

2.3 次固结沉降的计算

次压缩沉降也称为次固结沉降，发生在固结沉降之后，次固结沉降则是由土骨架蠕动变形所引起。许多室内试验和现场实测的结果都表明，次固结沉降的大小与时间的关系在半对数纸上接近于直线，因此，利用该直线关系可以得到次固结沉降。土体的次固结沉降是由土的流变性质引起的，软土在某级荷载作用下，次固结的大小与时间关系在半对数上接近直线，发生在主固结之后，次固结引起的孔隙比变化为：

则软土层厚度为H的地基次固结沉降为:

式中：t1为表示次固结的起始时间；t2为表示建筑物或构筑物的使用年限；Cd为次固结曲线的斜率，称为次固结指数；e0为初始孔隙比。

然而，需要指出的是，即使采用最先进的计算方法，也难以准确预估地基的沉降量，其原因在于：土工参数的可变性，外加荷载的大小、分布情况和描述应力分布及变形数学模型假设的不准确性。采用概率统计分析法在绝大多数概率统计分析中，均把表示压缩性和外荷载的量看成是随机变量或变量函数。这些变量都具有确定的从合适数据中导出的概率分布，然后将这些随机变量代入沉降等土工问题的计算公式中，就可获得沉降量的分布。这就是地基沉降量的概率统计分析法。除了以上介绍的几大类分析方法，还有不少学者应用新方法来预测软土地基的沉降量，如随机有限元法、人工神经网络法、灰色预测理论、一维或二维动态反演预测分析方法等。

3 结语

本文首先介绍了软土的特点和工程特性，指出深入探讨软土地基的沉降发展机理具有广泛的工程实际意义。详细介绍了饱和软土地基沉降计算中需要考虑的土体的自重应力计算、基底附加压力随地基沉降变化的影响、加载方式和加载速率的影响等关键问题，最后分别介绍了不同变形阶段的饱和软土地基总沉降量计算方法。■

[l]黄绍铭，高大钊.软土地基与地下工程[M].北京:中国建筑工业出版社，2005.

[2]谢定义.土动力学[M].西安:西安交通大学出版社，1988.

[3]BalighM M.LevadouxJN.Consolidation theory for eyelie loading [J].Journal of the G eotechnical D ivision，1980，106（5）:499-529.

[4]朱向荣，潘秋元.超载卸除后地基变形的研究[J].浙江大学学报，1991（2）：121-131.

[5]O hara S,etal.Study on the settlementof saturated layer induced by cyclic shear[J].Soil and Foundations,1988,28（3））:103-113.

[6]D utt,RathindraN.Cyclic behaviourof a deep-w ater normally consolidated clay[A].Proeeedings of the InternationalConference on CivilEngineering in the O eeans V[C].1992:546-59.

[7]Terzaghi K.Principles of soil mechanics[N].Eng.N aw s Record,D ec 17,1925.

[8]钱家欢，殷宗泽.土工原理与计算（第二版）[M].中国水利水电出版社，1996.

2012-03-06