基于图论的测量控制网拓扑分析系统的研究

宇 伟，李晓莉

(合肥工业大学土木与水利工程学院测量工程系，安徽合肥230009)

一、引 言

在研究测量控制网的机理、健康和安全时，首先需要解决的一个关键问题就是正确地识别或判断测量控制网工作时的图形参数，测量控制网的图形参数是研究控制网形变机理、健康监测和安全评估的基础和依据。测量控制网参数的识别属于系统识别范畴，一般意义上讲，就是在识别系统输入(激励)和输出(响应)数据的基础上，对系统确定一个数学模型，要求这个模型尽可能精确地反映测量控制网的结构特性，从而达到识别测量控制网系统的目的。基于图论的测量控制网拓扑分析系统是建立在系统输入和输出数据的基础上的，它实现了由控制网图形的映射、响应，以识别其图形参数，是一种方便、便宜和可行的方法，可以实现测量控制网的拓扑应用，具有明显的优点和显著的特色。

现在的测绘数据的处理一般是基于一定格式的观测文件，而后建立间接方程。通过观测文件的一定格式可以识别站点和其他点的拓扑关系，这是建立方程的基础。但是这种方式缺乏对整个控制网的拓扑分析，本文以图论为基础，旨在提高控制网拓扑分析能力，并建立相应的应用。

二、基于图论的控制网拓扑分析系统的设计

1．思 路

图论中点与点之间、点与线之间、线与线之间的拓扑关系主要有：①并联与邻联关系;②相交关系;③相离关系。如果两点存在联系可用直线相连两点，否则两点不连。测量控制网中，点与点之间、点与线之间及线与线之间的联系同图论中情况相似。测量控制网中，点与点间的联系参数包含高差、距离、角度，这就使控制网在拓扑识别的基础上还要建立与之相对应的观测数据文件，以建立观测值和测量控制网图形的映射关系，实现控制网的拓扑应用。

2．寻找拓扑形的算法过程

(1)数据结构的建立

在一般的仪器测量过程中，会产生以站点为结点的数据结构，可以在此数据结构上进行拓扑分析，也可以转化为其他的数据结构进行分析。本文以邻接矩阵来表示控制网的数据结构，并在其基础上按照一定的算法建立控制网的生成树，并在其基础上寻找闭合圈、附合路径等拓扑条件，再以整个测量控制网为基础，对控制网进行拓扑分析，这样可在拓扑形上进行数据处理，算法的基本过程如图1所示。

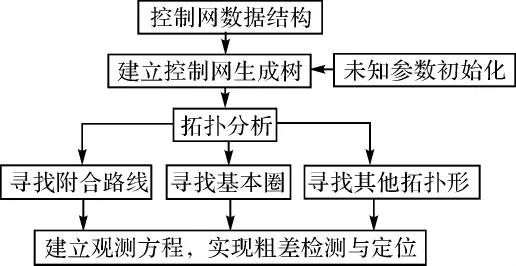
图1 算法的基本过程

(2)参数的初始化

未知参数的初始化主要是根据遍历控制网生成树进行的。遍历从已知点开始，按照广探法逐级遍历。即从已知点开始，将未知点初始化，再将其作为已知点初始化下一级未知点，直至未知点被全部初始化。

(3)附合路径的寻找

附合路径的寻找主要是寻找已知点和已知点间的路线，由于测量控制网中的已知点固定，可以建立从第一个已知点出发的广探法遍历，遍历的过程中建立记录遍历过程的数据结构，然后根据其他已知点在遍历中的次序，按一定算法找到附合路径。具体算法如下(若已知点数为n)：

1)从第一个已知点出发建立广探生成树，同时要记录生成树的路径。

2)生成树建立以后，根据其他已知点在遍历产生数据结构的位置，建立它们和第一个已知点的路径。

3)依次寻找n-1条路径为止。

(4)基本闭合圈的寻找

基本闭合圈是构成控制网中最基本非冗余的圈，即组成其他圈的最简单圈。基本圈的寻找要以控制网的生成树为基础，控制网中没有在生成树中的边会和生成树构成基本圈。具体算法如下：

1)按广探法建立控制网的生成树，同时要记录生成树的路径。

2)寻找出不在控制网生成树中的边。

3)根据构成这些边是两点进行回溯，直到回溯到同一点，建立起到该点的两条路径，合并这两条路径就组成基本圈。

(5)粗差的检测和定位

测量控制网的拓扑形状的识别，如闭合圈、附合路径均为多余条件，都可按一定的精度要求对拓扑形中的观测值进行粗差检测，如闭合差等。如果检测结果超限，则表明该拓扑形状中含有粗差。如果控制网中多个拓扑形状均反映出检测超限的情况，则粗差很可能出现在各拓扑形的交集上。其算法如下：

1)按照前述的算法找出各拓扑形。

2)按一定的精度要求对拓扑形进行检测。

3)若拓扑形出现粗差，进行交集分析，定位粗差的范围。

3．算法过程的主要代码

三、试验结果及分析

为使问题简便，现对一结点控制网展开讨论。某一控制网其网形(可取用水准网或是未记角度的导线网)，如图2所示，该网形的邻接矩阵(对称阵)为

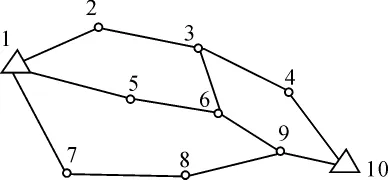
图2

首先由广探法建立控制网的生成树，进行初始化。通过拓扑分析后，可寻找到的拓扑形为：① 附合路线1，2，3，4，10; ② 闭合路线分别为：闭合圈一1，2，3，6，5，1，闭合圈二1，5，6，9，8，7，1，闭合圈三3，4，10，9，6，3。这些图形条件找出后，可以用于建立条件方程和误差分析等，如：如果5—6段存在粗差，则通过分析，粗差可能在1—5或5—6段;如果是6—9段存在粗差，则可直接确定6-9段。

四、结束语

在控制网数据处理中引入拓扑分析，增强了对控制网图形条件的使用，实现了数据处理的自动化和简单化，避免了繁杂的数据处理。由于引入拓扑分析，将改变方程建立模式，对控制网的精度和可靠性分析也会产生变化，如对控制网进行拓扑分析，这样可在拓扑形上进行数据处理，实现条件方程的建立和粗差的检测与定位等应用。然而，就控制网拓扑形寻找而言，也有其复杂性，如建立条件方程的圆周条件和极条件的寻找时就要同时利用观测文件和图论中的数据结构，或者建立特殊的数据结构，分析也是有一定的难度，但是对于一般的水准网、导线网及GPS网的拓扑分析还是比较简单的。

[1]项荣武，刘艳杰，胡忠盛．图论中最短路径问题的解法[J]．沈阳航空工业学院学报 ，2004，21(2)：86-88．

[2]朱力杰，杨元喜．论粗差修正与粗差剔除[J]．测绘通报，1999(6)：5-6．

[3]柴登峰，张登荣．前N条最短路径问题的算法及应用[J]．浙江大学学报：工学版，2002，36(5)：531-534．

[4]刘瓒武．应用图论[M]．长沙：国防科技大学出版社，2006．

[5]李明．数据结构(C++版)[M]．北京：清华大学出版社，2005．

[6]武汉大学测绘学院测量平差学科组．误差理论与测量平差基础[M]．武汉：武汉大学出版社，2009．