小地区GPS高程拟合的方法研究与实施

王 岩，刘茂华，党永超

(沈阳建筑大学土木工程学院，辽宁沈阳110168)

一、前 言

GPS测量以其速度快、精度高、全天候、操作简单等特点被越来越广泛的应用于平面控制测量工作中，并给测绘工作带来了巨大的变革。但是，由于受到高程异常的影响，其在高程测量工作中具有一定的局限性。

我国目前采用的高程系统是正常高高程系统，即以似大地水准面为基准面，以铅垂线为基准线的高程系统，而GPS高程测量所采用的高程系统是大地高高程系统，即以参考椭球面为基准面，以法线为基准线的高程系统。两者之间的关系如图1所示。

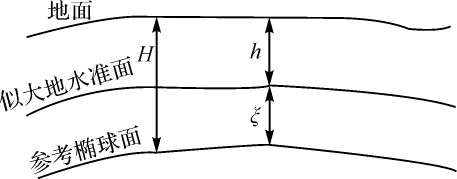
图1 正常高与大地高

要将GPS所测的大地高转化成我国所使用的正常高，就必须先求出参考椭球面与似大地水准面之间的差距，即高程异常ζ，然后根据大地高(H)求得正常高(H正常)，即

由于参考椭球面是一个规则的几何曲面，而似大地水准面受到重力等因素的影响，是一个不规则的曲面，所以每一个点上的高程异常ζ都各不相同。因此，精确求解高程异常值成为了提高GPS高程测量精度的关键之处。一般的，较大范围内精确的确定每一个点的高程异常值较为复杂，通行的方法是利用重力拟合法通过地面重力资料求解高程异常值。但是通常情况下，重力资料难以获得，因此此方法在工程中难以实施。

当测区范围相对较小时，由于地势变化不大，各方面的影响因素较为接近，因此可以认为高程异常具有一定的几何相关性。可以利用这一原理，建立相应的数学模型，并利用拟合法求解GPS所测各点的正常高[1]。所谓拟合法就是对GPS观测点进行几何水准联测，即先将同一点的大地高减去正常高得到该点的高程异常;再把测区的似大地水准面假定为多项式曲面或者其他数学曲面去拟合已知高程异常的点;最后根据拟合的曲面内插其他GPS点的高程异常值。利用拟合法进行GPS高程转换的数学模型很多，在小地区内通常采用平面拟合法、多项式曲面拟合法和多面函数拟合法等几种方法。由于平面拟合法一般仅适用于地势平坦地区，在其他情况下精度相对较低，因此本文对其不做讨论。

二、小地区GPS高程拟合的基本方法

1．多项式曲面拟合法

多项式函数拟合法的基本思想是：在小区域内的GPS网中，将似大地水准面看成曲面或平面，将高程异常表示为平面坐标(x，y)的函数，通过网中起算点已知的高程异常确定测区的似大地水准面形状，求出其余各点的高程异常，进而求出正常高，其数学模型为

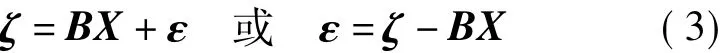
式中

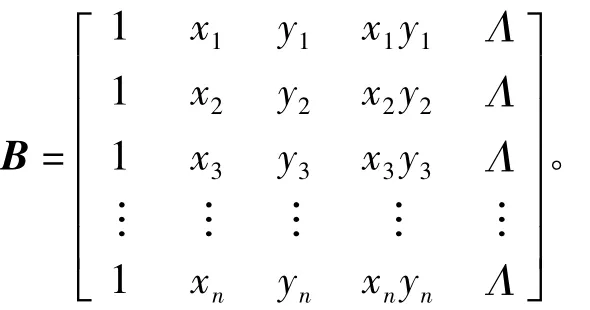
多项式拟合的实质是构造一个多项式函数，使得该多项式函数所代表的曲面尽可能逼近高程异常曲面。多项式函数理论上可以是二次、三次乃至N次，但是随着次数的增高，模拟曲面出现震荡现象，和实际的高程异常曲面相差较大。考虑到三次多项式最少需要10个已知点数据，而二次多项式理论上6个已知点即可拟合，所以通常选用二次多项式作为高程拟合曲面函数，即

2．多面函数拟合法

多面函数的基本思想是：任何数学表面和任何不规则的圆滑表面，总可以利用一系列规则的数学表面的总和以任意精度逼近。即在每个插值点上，同所有的已知数据点分别建立函数关系，并将这些多面函数的值叠加起来，以获得最佳的曲面拟合值。高程异常函数可表示为

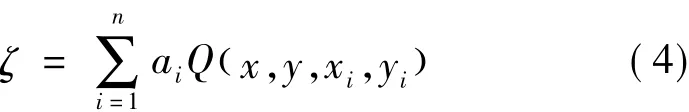
式中，Q(x，y，xi，yi)为核函数;ai待定系数，代表第 i个核函数对多层叠加面的贡献;n为简单数学面的张数或多层叠加面的层数，它的值与分块扩充范围内参与点的个数相等;x，y为待求点坐标，xi，yi为已知点坐标。核函数有多种形式，一般选择核函数

其中，δ为平滑因子。

三、小地区GPS高程拟合的实施

1．控制网的布设与观测

针对上述两种拟合方法，设计试验进行实例验证。如图2所示，试验场地选择在沈阳市东陵区，地势较为平坦，测区东西长约 2．5 km，南北宽约2．0 km，在测区内共布设13个GPS点，其中GP1和GP11点高程已知。GPS网基线平均长度约600m。

图2 GPS控制网略图

利用3台华测M600型GPS接收机，采用边连式进行观测，共观测11个闭合环。每个闭合环观测时段不少于45min，且卫星状况良好，同步观测时间段的卫星数均不少于6颗。将所测得数据利用Compass静态处理软件处理后获得每一个控制点的平差后高程值。

为了对拟合数据评定精度，利用TRIMBLE DINI12型数字水准仪以GP1和GP11点为基准点对各GPS点进行二等水准测量，经平差计算获得每点的正常高。各点的大地高与正常高高程值如表1所示。

表1 控制网观测成果m

2．两种拟合方法的精度对比[2]

为了对比拟合精度，首先假定以网中的GP1、GP2、GP3、GP4、GP6、GP7、GP11、GP12 8 个点作为已知点，其余5个点作为检核点进行拟合。分别采用二项式曲面拟合法和多面函数拟合法两种方法对其进行拟合，结果如表2所示。

从表2可以看出，在此区域内二项式曲面拟合法的残差值明显小于多面函数拟合法的残差值，即二项式曲面拟合法的精度要高于多面函数拟合法。通过计算其限差值可知，二项式曲面拟合法的精度已经达到四等水准测量精度要求，所以在此区域内，其结果可以代替四等水准测量。

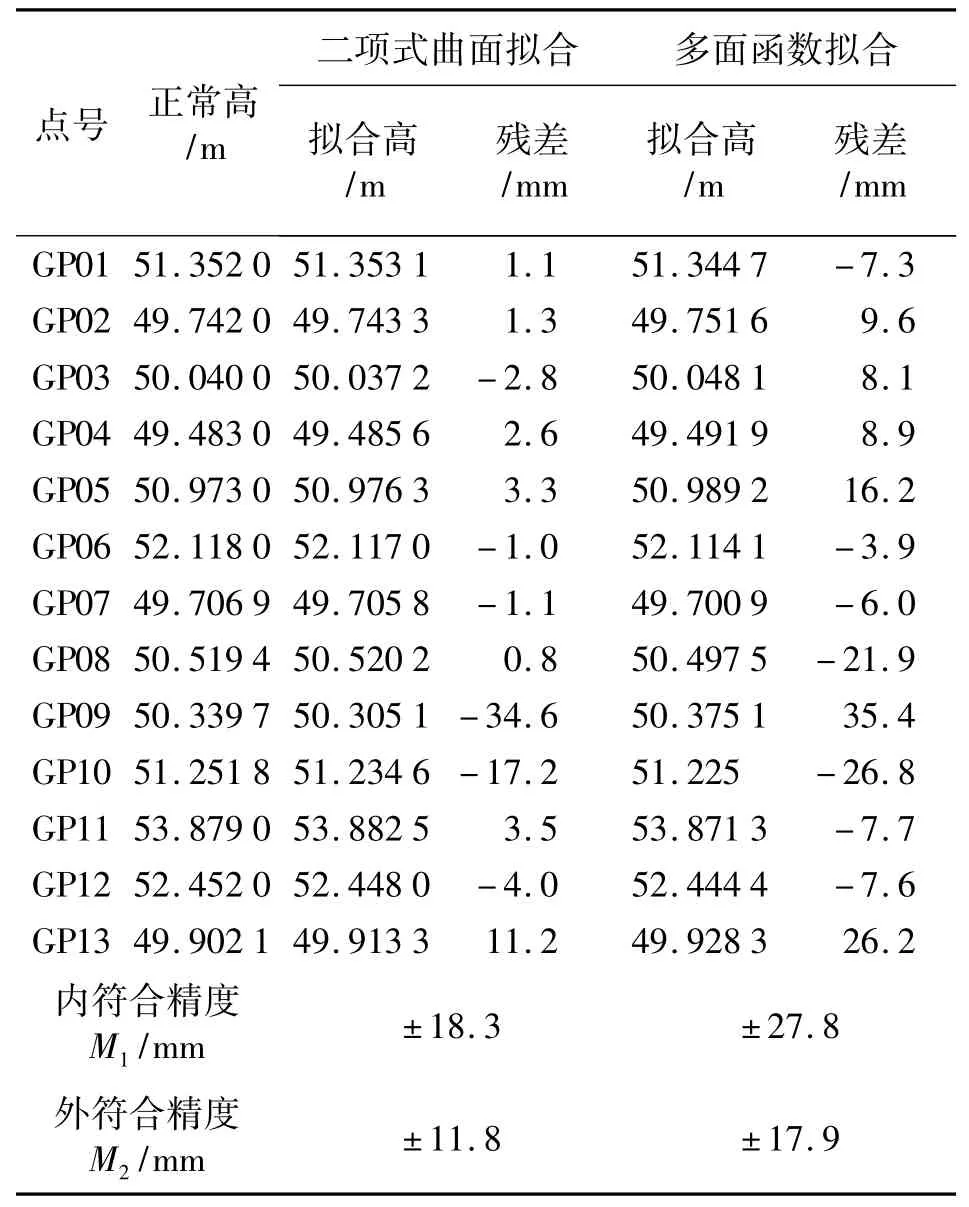
表2 二项式曲面拟合法与多面函数拟合法结果对比

就该实例来说，造成多面函数法精度较低的主要原因在于特征点点位较稀疏，多余观测较少。另一方面，在多面函数拟合模型程序化过程中确定的其核函数的中心点个数为6个，而在拟合计算过程中输入的已知点数为8个，多余观测仅有2个，这样就有可能因多余观测数不足而造成拟合精度不足。

3．同种方法选择不同已知点的对比

在工程中，已知点的位置对高程拟合的精度也有着较大的影响。为了直观说明此项影响，笔者利用同样的观测数据，选取不同的已知点进行拟合。此次假定以网中的 GP1、GP2、GP3、GP5、GP6、GP8、GP9、GP10 8个点作为已知点，其余8个点作为检核点进行拟合。仅以二项式曲面拟合法对其进行拟合，将所得结果与第三章第二节中二项式曲面拟合结果进行对比，如表3所示。

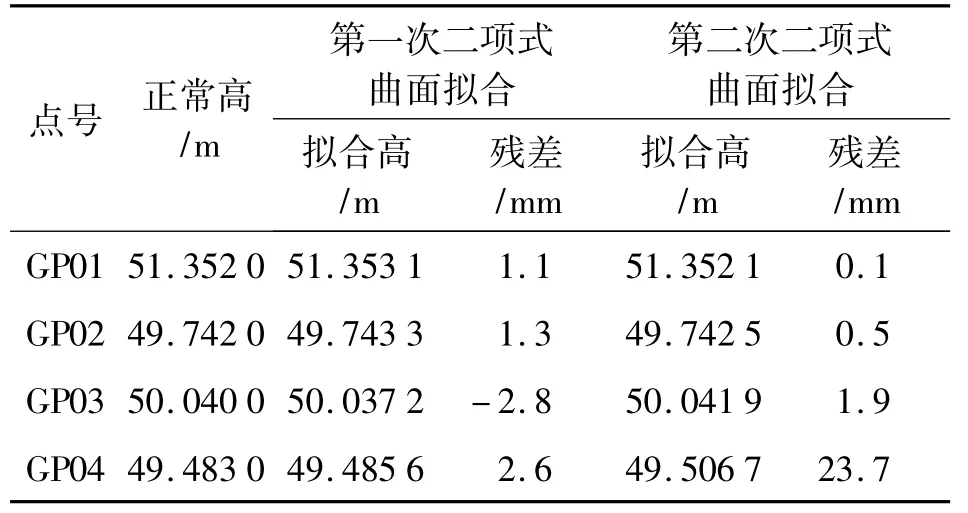
表3 选取不同已知点时二项式曲面拟合结果的对比

续表3

从表3中可以看出，第二次二项式曲面拟合的精度要小于第一次的拟合精度。主要原因在于第二次所选择的已知点并没有涵盖整个测区，且GP11、GP12等控制点的高程异常值并不是内插得到，而是外推得到的，由此造成了较大的误差。

四、结 论

根据上述试验数据经过分析可以得到以下结论：

1)由表2可以看出，二项式曲面拟合法比较适合地形单一高程变化较小的区域，其所需已知点个数较少，并且可以获得较高精度，实际工作中可操作性较强。

2)在地势较为平坦、已知点个数较少的前提下，二项式曲面拟合法比多面函数拟合法精度要高。

3)从表3可以看出，利用二项式曲面拟合法进行高程拟合时，已知点的选择对拟合精度有较大的影响。已知点应尽可能地覆盖整个测区，待定点在已知点覆盖范围之外时，拟合精度较低。

4)用数学函数进行GPS高程拟合都是一种近似的方法，无法做到精确求解每一点的高程异常值。因此，在选择数学模型以及选择起算数据时要充分考虑各类因素的影响，尽量提高拟合精度。

[1]高原，张恒璟，赵春江．多项式曲面模型在GPS高程拟合中的应用[J]．测绘科学，2011，36(3)：179-181．

[2]闫玮，高俊强，王维．小地区GPS高程拟合和水准测量对比试验[J]．南京工业大学学报，2007，29(5)：93-96．