一种基于非线性最小二乘的空间后方交会算法

余岸竹，姜 挺，江刚武，罗 胜，刘建辉

(信息工程大学地理空间信息学院，河南郑州450052)

一、引 言

摄影测量学中经典的空间后方交会算法是通过对成像时刻摄站的位置、姿态的近似值在一定的坐标系下描述后，对共线条件方程进行线性化，并结合一定数量的地面控制点及其像点，利用线性最小二乘平差方法迭代求解[1]。该解法的前提条件是给定的近似值与真值十分接近，在一定的精度下可以使用泰勒展开的一次项近似代替原始的非线性模型。当初值与真值差距较大时，该方法会带来一定的模型误差，甚至出现迭代不收敛的情况。如何提高后方交会的精度一直摄影测量定位中的一个热点问题[2-4]。为降低线性化带来的影响，本文结合非线性平差模型，提出一种基于非线性最小二乘的空间后方交会算法，通过试验验证该方法的有效性。

二、基于非线性最小二乘的空间后方交会原理

1．非线性最小二乘平差方法

非线性最小二乘平差方法与传统的最小二乘平差方法有类似的目标函数。设 ^X表示待求参数的估计值，V表示改正数，L表示观测值向量，则原始误差方程可写为

式中，f为一非线性函数模型。最小二乘法解算方法是在(1)的条件下，答解目标函数[6]

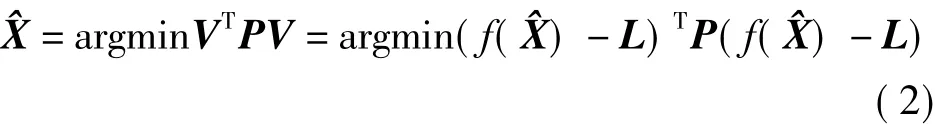
式(2)可进一步化简为

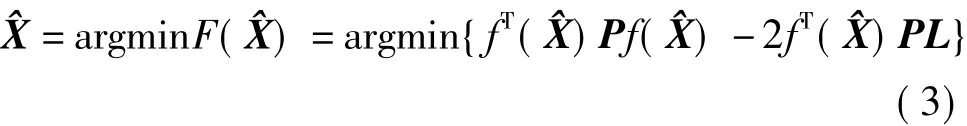
由于式(3)中f是一个非线性函数，因此根据矩阵求导的链式法则[7]可知

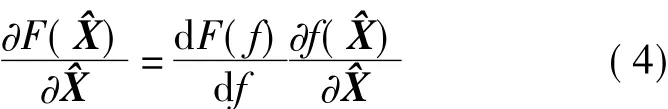
2．数学模型

使用欧拉角描述摄站姿态时，空间后方交会待答解的外方位元素矢量为 M=(Xs，Ys，Zs，φ，ω，κ)T，则共线条件方程可表示为[1]

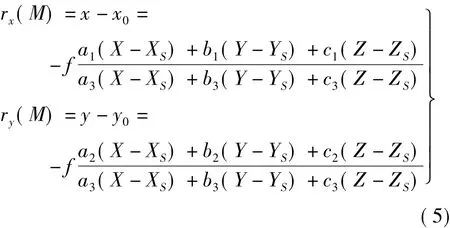
式中，(x0，y0，f)为像片的内方位元素;(x，y)表示像点坐标;(X，Y，Z)为像点对应的地面点坐标;参数ai，bi，ci是由(φ，ω，κ)组成的旋转矩阵对应的元素。

令

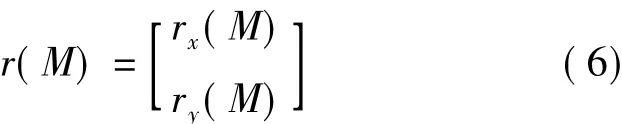
将上式代入式(3)可得

设M(0)为 M的一个近似值，即 M=M(0)+d M(0)。当观测误差满足高斯-马尔可夫条件时，可假定权矩阵P为单位矩阵，此时，将函数F(M)在M=M(0)处泰勒展开至二次项得

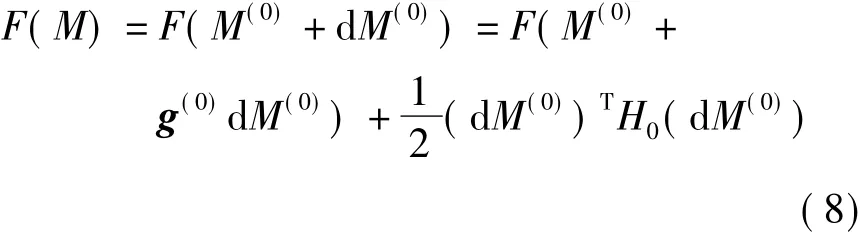
式中，g(0)和H0分别是F(M)是M=M(0)的梯度矢量与Hessian矩阵，其表达式为

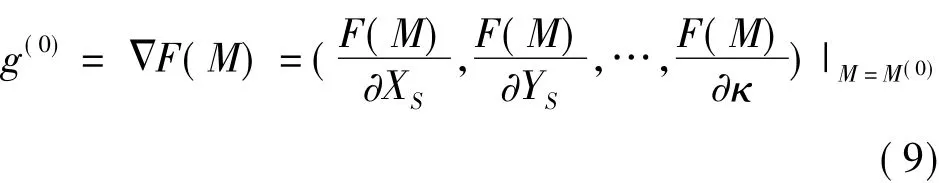
及

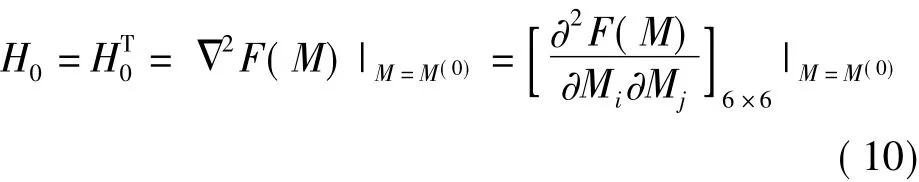
式中，Mi(i=1，2，…，6)是外方位元素矢量M的第i个元素。为了求得使式(8)最小的d M(0)，将该式对d M(0)求偏导并令其等于零，得

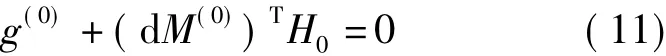
当H0满秩时，可以求出

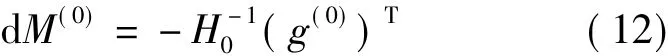
则

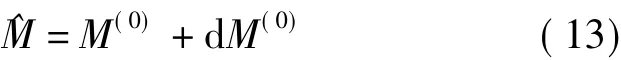
将 ^M作为新的近似值M进行迭代答解，直到‖d M(0)‖小于给定的阈值，即可求得非线性最小二乘法则下 ^M的最优值。

三、试验结果与分析

为了非线性最小二乘答解空间后方交会的有效性，并与经典的后方交会算法进行对比，使用文献[2]中郑州某地区的真实影像数据进行试验，其具体参数如表1所示，控制点分布情况如图1所示，控制点具体坐标如表2所示。

表1 航空影像参数

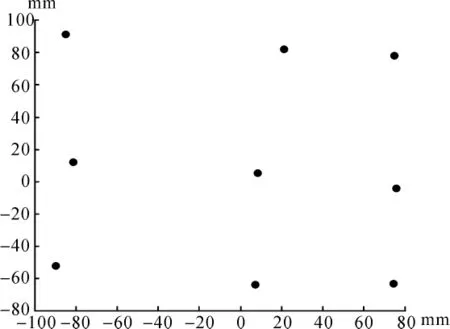
图1 控制点分布略图

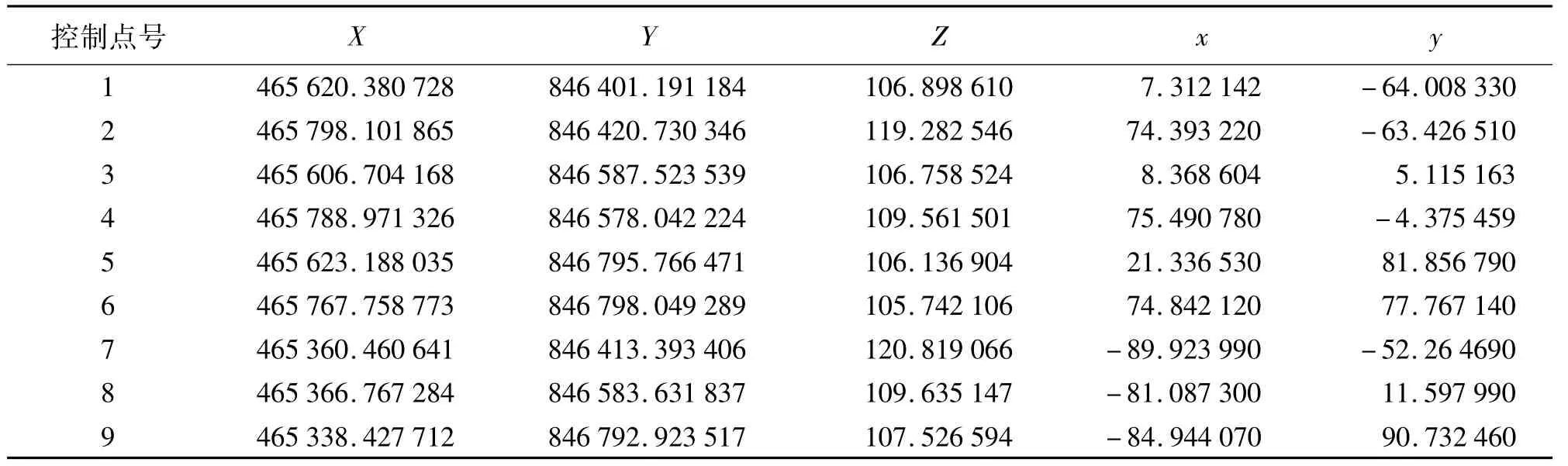
表2 实际地面控制点m

利用本文提出算法、文献[2]算法与经典算法分别对真实影像进行空间后方交会，初始值按照文献[9]中给定的空间后方交会初值选取，结果如表3所示。

表3

从表3的解算结果可以看出，基于非线性最小二乘的解算方法、基于四元数的算法和传统方法的解算精度相当，最大线元素之差约为0．016 m，最大角元素之差约为0．001°，验证了本文算法的有效性。

四、总 结

空间后方交会是摄影定位中的关键步骤。为减少由线性化带来的模型误差，本文提出了基于非线性最小二乘的空间后方交会算法，并使用真实影像数据证实了提出算法的有效性，可以与传统算法和基于四元数的算法达到相当的精度。然而还有以下问题需要进行进一步研究：

1)答解优化问题过程中，需要求解Hessian矩阵，其求解计算复杂度较大，降低了答解的效率，如何对算法进行优化需要深入研究。

2)仅验证了该算法在近似垂直摄影情况下的有效性，而在不同倾角、不同航高的成像条件下的收敛性需要深入探讨。

3)文献[10]中证明了非线性最小二乘解算结果既不是真值的无偏估计量也不是最小方差有偏估计量。因此，如何改进估计量的统计性质是进一步研究的方向之一。

[1]WANG Zhizhuo．The Principles of Photogrammetry[M]．Beijing：Press of Surveying and Mapping，1990．

[2]龚辉，姜挺，江刚武，等．一种基于四元数的空间后方交会全局收敛算法[J]．测绘学报，2011，40(5)：639-645．

[3]Jl Qiang，MAURO SC，ROBERT M H，et a1．A Robust Linear Least-squares Estimation of Camera Exterior Orientation Using Multiple Geomatric Features[J]．ISPRS Journal of Photogrammetry and Remote Sensing．2000，55：75-93．

[4]FIORE PD．Efficient Linear Solution of Exterior Orientation[J]．IEEE Transactions on PAMI，2001，23(2)：140-148．

[5]王新洲，陶本藻，邱卫宁，等．高等测量平差[M]．北京：测绘出版社，2006．

[6]隋丽芬，宋力杰．误差理论与测量平差基础[M]．北京：解放军出版社，2004．

[7]张贤达．矩阵分析与应用[M]．北京：清华大学出版社，2004．

[8]马昌凤．最优化方法及其Matlab程序设计[M]．北京：科学出版社，2010．

[9]张保明，龚志辉，郭海涛．摄影测量学[M]．北京：科学出版社，2008．

[10]王新洲．非线性模型参数估计理论与应用[M]．武汉：武汉大学出版社，2002．