基于STK的探月飞行轨道仿真

杜 兰，王若璞，张中凯，王占统

(信息工程大学导航与空天目标工程学院，河南郑州450052)

对于月球测绘科学及其应用的发展，发射探月飞行器是十分必要的。嫦娥一号是我国的首颗绕月卫星，于北京时间2007年10月24日18时05分在西昌卫星发射中心升空，到进入月球的圆极轨道共历时14 d[1]。嫦娥一号卫星的飞行轨道主要由发射段、调相段、地月转移段和月球捕获段等4部分轨道构成。

一、轨道仿真的设计思路

由于公开资料提供的数据有限，大部分设计参数(如轨道机动参数等)需要使用STK的Target工具进行迭代搜索计算。此外，轨道仿真没有按照时间顺序构建分段轨道，而是采用正向和逆向相结合的流程(如图1所示)。

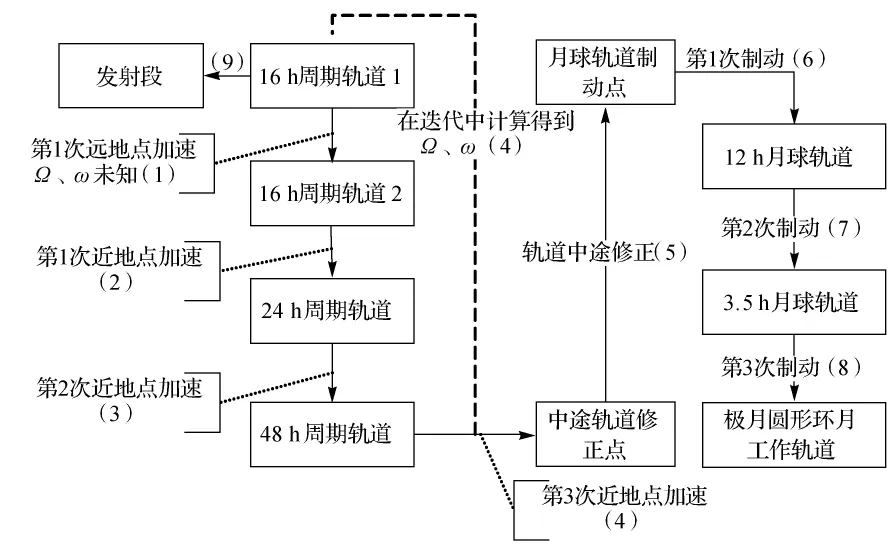
图1 轨道仿真设计流程图

对于发射段，由于资料数据不足，未知参数达到5个，无法通过Target工具迭代计算。所以初步设计时先跳过发射段，从卫星的驻留轨道(即图1的16 h周期轨道1)起算。

3个调相轨道段，即图1中的(1)～(3)，都是基于拱点的共面变轨，变轨冲量基本不受未知的轨道根数Ω和ω影响。因此，这里采用了概略值，并将通过后续的地月转移段来反算得到修正值。

奔月段(包括一次中途轨道修正)是STK仿真的关键设计段。主要是通过3步从松到紧的约束，逐渐逼近近月轨道段的制动点，并同时得到轨道根数Ω和ω的准确值。

月球俘获段由于基本参数均已获得，仿真较简单。

最后一步是反算发射段的机动参数。

二、STK/Astrogator/Target构建

Astrogator轨道机动模块是STK的12个积分器之一，它主要提供了一个交互式的轨道机动和太空任务计划工具[5]。Target的工作原理是利用牛顿迭代法求解满足约束条件方程F(→x)=→y的控制参数→x(通常为轨道设计参数和机动参数)。由于是迭代算法，Target收敛通常要求满足两个条件：一是为控制参数→x提供一定精度的概略初值;二是约束条件方程的微分改正系数矩阵应具有较好的线性特性。反映在Target序列中，主要是通过设计和调节一系列target profiles，利用由松到紧的约束来逐步精化轨道制动参数。

嫦娥一号飞行轨道使用了两个Target来进行构建。第一个Target将调相轨道和地月转移轨道合在一起进行设计参数搜索;第二个Target仅为月球捕获机动搜索。两者完成后再插入发射段。图2给出了第一个Target的任务控制序列;表1列出了两个Target中的参数设置，其中力模型CisLunar考虑了地月转移期间地球和月球的共同影响。

由于卫星发射段资料数据少，无法直接模拟。但经过前面Target1计算，可以得到卫星进入最初驻留轨道即入轨点的位置速度，同时也是发射段关火状态。利用已知的点火条件和关火状态便可以进行发射段轨道模拟。

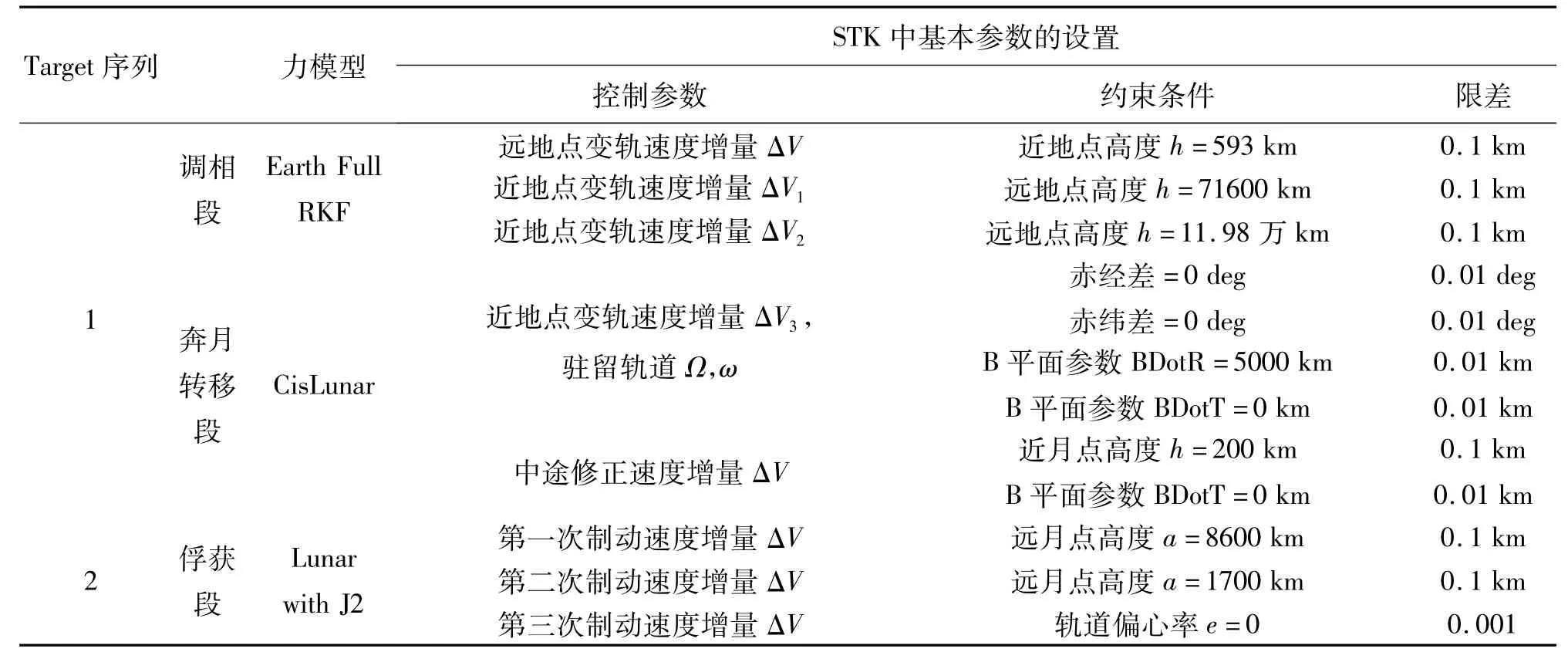
表1 STK/Astrogator/Target的参数设置

需要注意，在Target自动计算任务设计参数的迭代过程中，约束条件的设置至关重要。约束条件松紧不同，则结果不同，有时甚至影响迭代的成功与否。

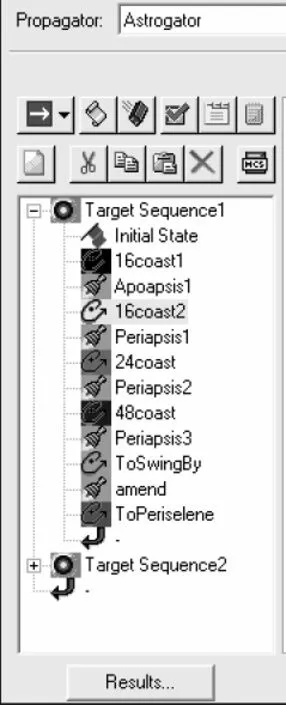
图2 Astrogator任务控制序列

表1中给出了每次Target的约束条件及限差。查看其中奔月转移段的第3次近地点变轨，为保证STK缺省的25次迭代计算能够收敛，设计了一松一紧的两个profile约束条件来逐步精化轨道。前者利用飞行方向与月球赤经和赤纬差为零的约束来调整驻留轨道的空间指向对准月球;后者则在此基础上利用B平面参数进一步精化控制参数。此外，限差的调节也会对迭代速度产生较大影响。

三、仿真结果

与实际数据对比表明，STK轨道模拟与实际轨道在时间节点及轨道形式上基本相同。表2中，在调相段末段出现了1 h时差，主要是由于仿真卫星变轨采用的是理想瞬时冲量，而非真实的持续推力，二者改变速度的推进机制不同;在地月转移段出现了6 h时差，除了奔月变轨方式的原因外，还包括前段仿真“误差”在轨道外推过程中累积的原因。

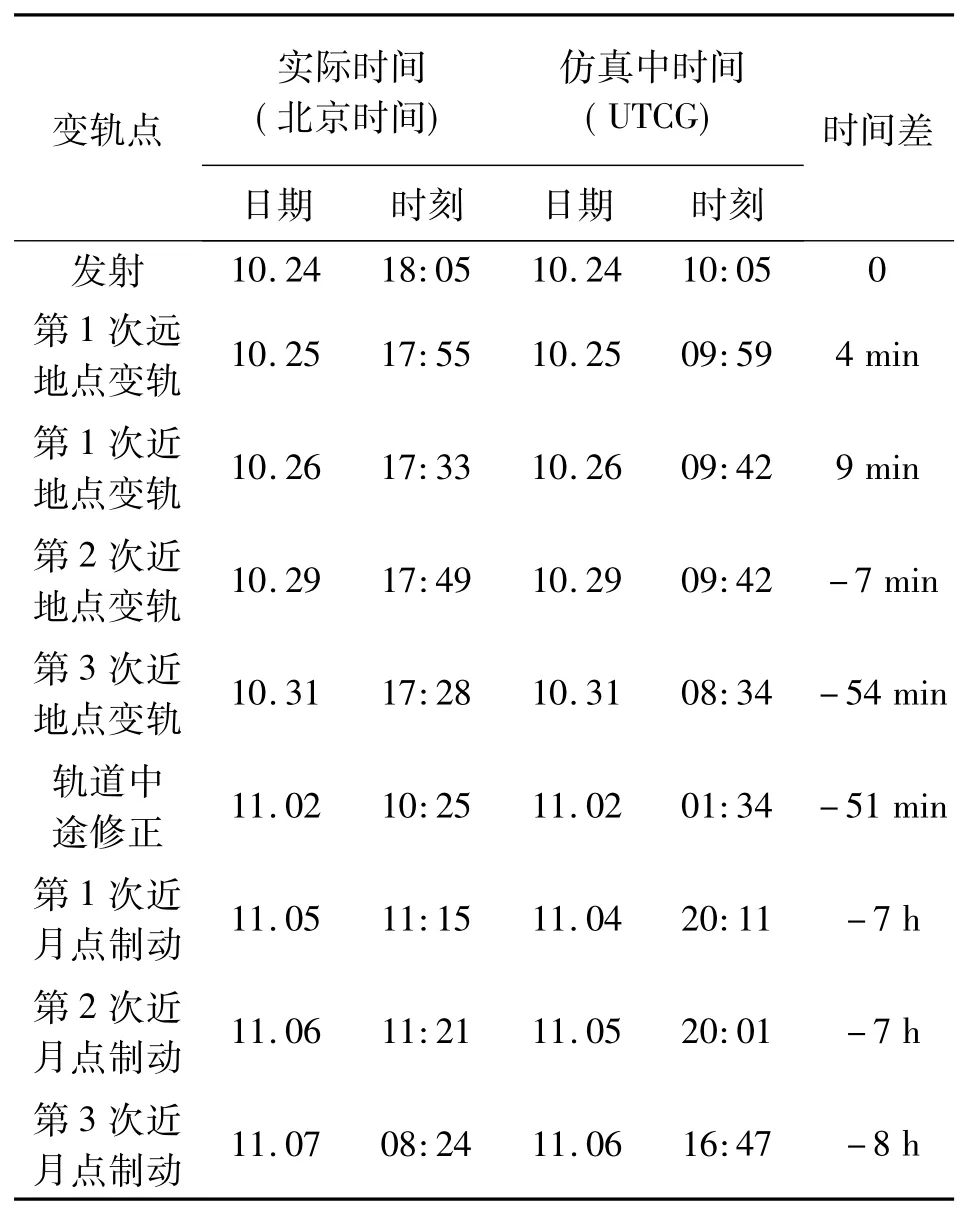
表2 仿真中变轨点时间与实际时间对比

STK仿真能够直观地反映不同视角和坐标系下的嫦娥一号飞行轨道。图3为保持地月连线不动的BBR坐标系下的飞行轨迹;图4则显示了同一视场和坐标系下3次月球俘获制动段的轨迹放大效果。

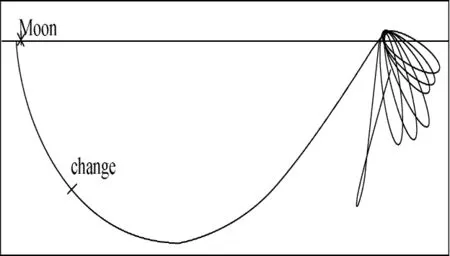
图3 地月旋转坐标下的飞行轨迹

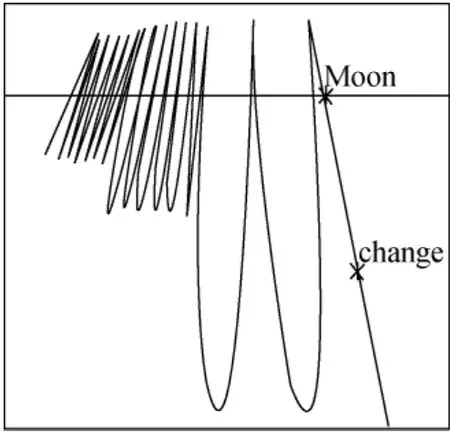
图4 放大后的月球捕获段轨迹

四、结束语

月球探测的轨道设计较为复杂，需要精心选取发射窗口。STK虽然不适用于大批量设计的全局最优搜索，但是一旦确定了发射参数，STK软件则充分显示了其对特定飞行任务仿真的便利性和高度自动化，可以有效地建立复杂力模型下的月球和行星际飞行轨道，尤其是转移过程中的若干次中途修正和影响球内的逃逸段和俘获段。本文方法同样适用于嫦娥二号和待发射的嫦娥三号的部分轨道段仿真。

[1]天鲁．嫦娥—1的奔月之路[J]．国际太空，2007(12)：13-21．

[2]刘林，王歆．月球探测器轨道力学[M]．北京：国防工业出版社．2006．

[3]HOWARD D C．轨道力学[M]．北京：科学出版社，2009：277-318．

[4]杜兰，张浚哲，王丹丹，等．萤火一号火星探测器的轨道设计和 STK仿真[J]．测绘科学技术学报，2009，26(4)：235-237．