用泰勒级数展开法求解等量纬度反解问题的新方法

常国宾，欧阳永忠，李胜全，金际航，李 科

(海军海洋测绘研究所，天津300061)

一、引 言

等量纬度是地图投影理论中的一种重要辅助纬度，它是大地纬度的函数，在地图制图、大地测量和地球物理等领域应用十分广泛[1-6]。一般由大地纬度求解等量纬度的过程称为等量纬度的正解问题，反之，则为反解问题。等量纬度的反解函数是复杂的隐函数，求解方法主要有迭代法和直接法，直接法便于采用和理论分析。在公开发表的文献中，等量纬度反解问题的直接求解方法大致分为4种，分别为等量纬度的麦克劳林级数展开[6]、偏心率的麦克劳林级数展开[7-8]、拉格朗日级数展开[5，9]、埃尔米特插值法[10-13]，其中，用埃尔米特插值法得到的公式其精度为最高。泰勒级数是麦克劳林级数的广义形式，麦克劳林级数是一种在初值为0处的特殊泰勒级数，当要处理的值距离0较远时，麦克劳林级数存在收敛较慢的问题，而泰勒级数可以通过合理地选择展开初值避免此问题。鉴于此，本文尝试利用泰勒级数展开法求解等量纬度的反解问题，其中展开初值的选取方法为：在假设偏心率为0的情况下，由等量纬度解析得到球心纬度作为大地纬度的初值，将球心纬度代入等量纬度的正解公式得到等量纬度初值。将等量纬度反解隐函数在等量纬度和大地纬度的初值处进行泰勒级数展开就可以得到等量纬度的反解公式，该公式为等量纬度和偏心率的函数。整个推导过程由强大的Mathematica计算机代数系统[10]完成，推导结果由计算机存储，无需人工推导和记忆，且可以根据精度和计算成本灵活选择泰勒级数展开的阶数。试算结果表明，该方法具有明显的精度优势。

二、等量纬度正、反解问题

等量纬度与大地纬度之间的微分关系为

式中，q为等量纬度;B为大地纬度;e为第一偏心率。以B为积分变量，对上式进行积分可以得到

特别的，当e为0时，大地纬度B变为球面纬度φ，则有

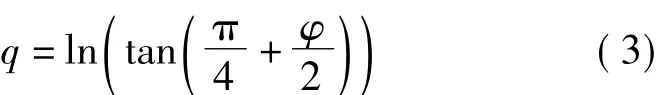
因此有

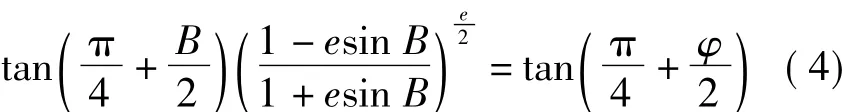
对上式进行处理，即可以得到φ与B的关系式，一般为如下形式

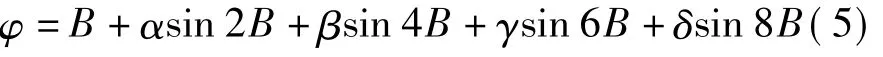
式(3)和式(5)即为等量纬度正解展开公式，文献[10]利用Mathematica计算机代数系统对上述系数进行了推导，纠正之前人工推导的系数中存在的错误。

假设等量纬度反解函数为如下形式

则有

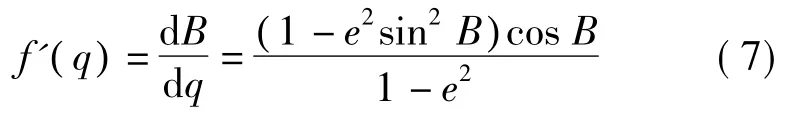
华棠对式(6)在q=0(对应的，B=0)处进行泰勒级数展开(即麦克劳林级数展开)，并利用式(7)所示的关系，得到了实用的等量纬度反解公式。

边少锋等从新的角度对等量纬度反解公式进行了研究，在文献[10]中，首先根据三角级数回求公式确定式(6)的具体形式为

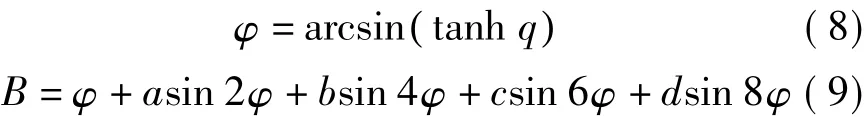
然后利用埃尔米特插值法确定式(9)中的各系数。

试算结果表明边少锋等推求的公式其精度优于前人得到的公式。

三、用泰勒级数展开法求解等量纬度反解公式的新方法

麦克劳林级数是泰勒级数在初值为0处的特殊形式。如果所处理的值距离0较远，则麦克劳林级数收敛速度较慢，甚至可能发散。而如果合理地选择初值，泰勒级数则具有较快的收敛速度，在相同的阶数下，具有更高的函数近似精度。因此，相比传统方法中对式(6)进行麦克劳林级数展开，在合适的初值处对式(6)进行泰勒级数展开，理论上可以得到更优的结果。

对一函数进行泰勒展开，首先需要确定展开初值，在等量纬度反解问题中，也就是确定B和q的初值B0和q0。

令e=0，则根据式(1)可以得到

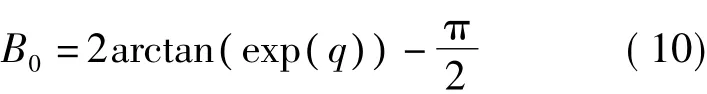
或者

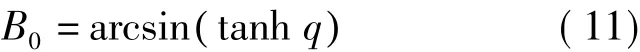
将大地纬度初值代入式(5)，然后再代入式(3)则可以得到B0对应的等量纬度初值q0，即

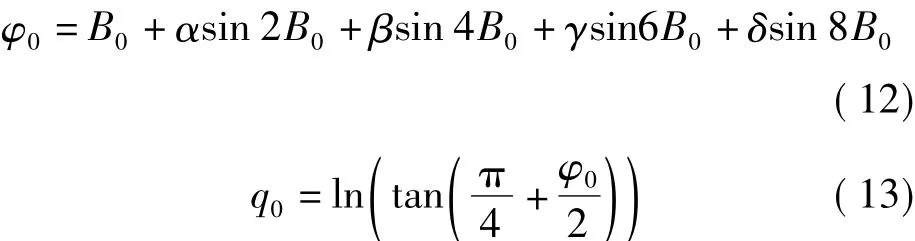
求式(6)在B0和q0处的各阶导数值

对式(6)在B=B0、q=q0处进行N阶泰勒级数展开得

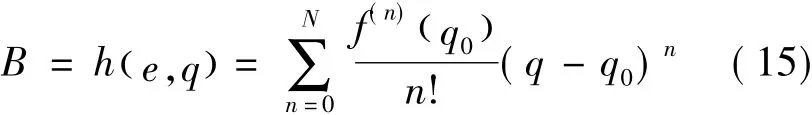
式(11)～式(15)即为由q求解B的过程，整个推导过程由Mathematica计算机代数系统自动完成，推导结果由计算机存储，无需人工推导和记忆。公式为偏心率和等量纬度的函数，可以根据不同的参考椭球模型代入不同的偏心率，此外，还可以根据对精度和计算成本的不同要求选择不同的阶数N。

四、计算实例

为了验证本文方法的有效性，对等量纬度正、反解试算，其中反解过程中分别采用文献[10，12]的方法和本文的方法，以比较两种方法精度。验证过程为：给定一大地纬度B，将B代入式(5)，然后再代入式(3)，得到q，然后分别将q代入式(8)、式(9)以及式(11)～式(15)得到 B1和B2，分别比较B1和B的差、B2和B的差。对几种不同参考椭球的椭球参数进行了试算，得到的结论是相同的，简便起见，只列出 WGS-84椭球基本常数 e=0．006 694 379 990 14的试算结果，如表1所示，其他参考椭球的试算结果不再赘述。

表1 WGS-84椭球等量纬度反解数据验证

由表1的试算结果可以发现，本文方法在阶数取到4时，其精度就已经全面超越传统方法的精度，当阶数取到5时，本文方法的精度几乎在所有取值处都超过传统方法一个数量级以上。由阶数取6和阶数取7的试算结果对比可以发现，当阶数取到6以上时，其精度达到稳定，计算机的舍入误差超过泰勒级数的截断误差，成为主要部分，精度不再随阶数的增加而提高。

五、结束语

本文采用泰勒级数展开法对等量纬度反解问题进行了新的研究，通过合理选择展开初值，本文方法可以得到更为优越的反解精度。本文方法具有如下几个方面的优势：一是推导过程由Mathematica计算机代数系统完成，推导结果由计算机存储，无需人工推导和记忆;二是推导的公式是偏心率的函数，可以灵活地应用于不同的参考椭球模型;三是在选定偏心率时，公式是等量纬度的函数，可以直接将等量纬度代入，无需迭代;四是精度明显优于传统方法;五是可以根据精度和计算成本的要求，灵活选择泰勒级数展开的阶数。本文方法还可以用于等面积纬度、等距离纬度等其他辅助纬度的反解问题，并可用于地图投影等领域。

[1]SNYDER J．Map Projections-A Working Manual[M]．Washington DC：Government Printing Office，1987．

[2]YANG Q，SNYDER J，TOBLER W．Map Projection Transformation：Principles and Applications[M]．Florida：CRC Press，1999．

[3]BOWRING B．The Direct and Inverse Problems for Short Geodesic Lines on the Ellipsoid[J]．Surveying and Mapping，1981，41(2)：135-141．

[4]熊介．椭球大地测量学[M]．北京：解放军出版社，1988．

[5]杨启和．地图投影变换原理与方法[M]．北京：解放军出版社，1989．

[6]华棠．海图数学基础[M]．北京：海潮出版社，1985．

[7]边少锋，纪兵．等距离纬度等量纬度和等面积纬度展开式[J]．测绘学报，2007，36(2)：218-223．

[8]BIAN Shao Feng，CHEN Yong Bing．Solving an Inverse Problem of a Meridian Arc in terms of Computer Algebra System[J]．Journal of Surveying Engineering，2006，132(1)：153-155．

[9]王瑞，李厚朴．辅助纬度反解公式的拉格朗日级数法推演[J]．海洋测绘，2008，28(3)：18-23．

[10]边少锋，许江宁．计算机代数系统与大地测量数学分析[M]．北京：国防工业出版社，2004．

[11]纪兵，边少锋．大地主题问题的非迭代新解[J]．测绘学报，2007，36(3)：269-273．

[12]李厚朴，边少锋．等量纬度展开式的新解法[J]．海洋测绘，2007，27(4)：6-10．

[13]李厚朴，边少锋．辅助纬度反解公式的埃尔米特插值法新解[J]．武汉大学学报：信息科学版，2008，33(6)：623-626．